Która transformacja nie prowadzi do utraty korzeni. Transformacja równań, transformacje równoważne. Zgodnie z warunkami DL
Temat równań trygonometrycznych rozpoczyna się od wykładu szkolnego, który ma formę rozmowy heurystycznej. Na wykładzie omawiany jest materiał teoretyczny oraz przykłady rozwiązywania wszystkich typowych problemów zgodnie z planem:
- Najprostsze równania trygonometryczne.
- Podstawowe metody rozwiązywania równań trygonometrycznych.
- Równania jednorodne.
Na kolejnych lekcjach rozpoczyna się samodzielny rozwój umiejętności, oparty na zastosowaniu zasady wspólnego działania nauczyciela i ucznia. W pierwszej kolejności wyznaczane są cele dla uczniów, tj. zdeterminowane jest, kto nie chce wiedzieć więcej, niż wymagają tego standardy państwowe, a kto jest gotowy zrobić więcej.
Diagnoza końcowa tworzona jest z uwzględnieniem zróżnicowania poziomów, co pozwala uczniom świadomie określić minimalny poziom wiedzy niezbędny do uzyskania oceny „3”. Na tej podstawie dobierane są wielopoziomowe materiały służące do diagnozy wiedzy uczniów. Taka praca pozwala na indywidualne podejście do uczniów, włączając wszystkich w świadome działania edukacyjne, rozwijając umiejętności samoorganizacji i samokształcenia oraz zapewniając przejście do aktywnego, samodzielnego myślenia.
Seminarium prowadzone jest po przećwiczeniu podstawowych umiejętności rozwiązywania równań trygonometrycznych. Na kilka lekcji przed seminarium studenci otrzymują pytania, które będą omawiane w trakcie seminarium.
Seminarium składa się z trzech części.
1. Część wprowadzająca obejmuje cały materiał teoretyczny, w tym wprowadzenie do problemów, które pojawią się przy rozwiązywaniu złożonych równań.
2. W drugiej części omówiono rozwiązanie równań postaci:
- i cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- równania rozwiązywalne poprzez zmniejszenie stopnia.
W równaniach tych zastosowano uniwersalne podstawienie, wzory redukcji stopni i metodę argumentów pomocniczych.
3. Część trzecia omawia problematykę utraty korzeni i nabywania korzeni obcych. Pokazuje, jak wybrać korzenie.
Uczniowie pracują w grupach. Aby rozwiązać przykłady, wzywa się dobrze przeszkolonych chłopaków, którzy mogą pokazać i wyjaśnić materiał.
Seminarium przeznaczone jest dla studenta dobrze przygotowanego, ponieważ... porusza kwestie nieco wykraczające poza zakres materiału programowego. Obejmuje równania o bardziej złożonej postaci, a zwłaszcza omawia problemy napotykane przy rozwiązywaniu złożonych równań trygonometrycznych.
Seminarium odbyło się dla uczniów klas 10-11. Każdy uczeń miał okazję poszerzyć i pogłębić swoją wiedzę na ten temat, porównać poziom swojej wiedzy nie tylko z wymaganiami stawianymi absolwentowi szkoły, ale także z wymaganiami stawianymi przystępującym do V.U.Z.
SEMINARIUM
Temat:„Rozwiązywanie równań trygonometrycznych”
Cele:
- Uogólnienie wiedzy na temat rozwiązywania równań trygonometrycznych wszystkich typów.
- Skoncentruj się na problemach: utrata korzeni; obce korzenie; wybór korzenia.
PODCZAS ZAJĘĆ.
I. Część wprowadzająca
1. Podstawowe metody rozwiązywania równań trygonometrycznych
- Faktoryzacja.
- Wprowadzenie nowej zmiennej.
- Funkcjonalna metoda graficzna.
2. Niektóre typy równań trygonometrycznych.
- Równania sprowadzające się do równań kwadratowych w odniesieniu do cos x = t, sin x = t.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Bsinx + C = 0.
Rozwiązuje się je poprzez wprowadzenie nowej zmiennej.
- Równania jednorodne pierwszego i drugiego stopnia
Równanie pierwszego stopnia: Asinx + Bcosx = 0 podziel przez cos x, otrzymamy Atg x + B = 0
Równanie drugiego stopnia: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 podziel przez cos 2 x, otrzymamy Atg 2 x + Btgx + C = 0
Rozwiązuje się je poprzez faktoryzację i wprowadzenie nowej zmiennej.
Obowiązują wszystkie metody.
- Nachylenie:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Rozwiązanie metodą faktoryzacji.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Równanie postaci: A(sinx + cosx) + Bsin2x + C = 0.
Zredukowane do kwadratu w odniesieniu do t = sinx + cosx; grzech2x = t 2 – 1.
3. Formuły.
x + 2 n; Sprawdzenie jest wymagane!
- Malejąca moc: cos 2 x = (1 + cos2x): 2; grzech 2 x = (1 – cos 2x): 2
- Metoda argumentacji pomocniczej.
Zastąpmy Acosx + Bsinx Csin (x + ), gdzie sin = a/C; cos=v/c;
– argument pomocniczy.
4. Zasady.
- Jeśli widzisz kwadrat, obniż stopień.
- Jeśli zobaczysz kawałek, zrób kwotę.
- Jeśli widzisz kwotę, wykonaj pracę.
5. Utrata korzeni, dodatkowe korzenie.
- Utrata korzeni: podziel przez g(x); niebezpieczne formuły (uniwersalna substytucja). Dzięki tym operacjom zawężamy zakres definicji.
- Dodatkowe korzenie: podniesione do równej mocy; pomnóż przez g(x) (pozbądź się mianownika). Dzięki tym operacjom rozszerzamy zakres definicji.
II. Przykłady równań trygonometrycznych
1. Równania w postaci Asinx + Bcosx = C
1) Uniwersalna substytucja.O.D.Z. x – dowolne.
3 grzech 2x + cos 2x + 1= 0.
tgx = ty. x/2 + n;
![]() u = – 1/3.
u = – 1/3.
tan x = –1/3, x = arctan (–1/3) + k, k Z.
Badanie: 3sin( + 2n) + cos( + 2n) + 1= 3 grzech + cos + 1 = 0 – 1 + 1 = 0.
x = /2 + n, n e Z. Jest pierwiastkiem równania.
Odpowiedź: x = arctan(–1/3) + k, k Z. x = /2 + n, n Z.
2) Funkcjonalna metoda graficzna. O.D.Z. x – dowolne.
Sinx – cosx = 1
Sinx = cosx + 1.
Narysujmy funkcje: y = sinx, y = cosx + 1.

Odpowiedź: x = /2 + 2 n, Z; x = + 2k, k Z.
3) Wprowadzenie argumentu pomocniczego. O.D.Z.: x – dowolne.
8cosx + 15 sinx = 17.
![]()
8/17 cosx + 15/17 sinx = 1, ponieważ (8/17) 2 + (15/17) 2 = 1, to istnieje takie, że grzech = 8/17,
cos = 15/17, co oznacza sin cosx + sinx cos = 1; = arcsin 8/17.
Odpowiedź: x = /2 + 2n – , x = /2 + 2n – arcsin 8/17, n Z.
2. Zmniejszenie rzędu: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). grzech 2 3x + grzech 2 4x + grzech 2 6x + grzech 2 7x = 2. O.D.Z.: x – dowolne.
1 – cos 6x + 1 – cos 8x + 1 – cos 12x + 1 – cos 14x = 4
sałata 6x + sałata 8x + sałata 12x + sałata 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x(cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Odpowiedź: x = /20 + n/10, n Z. x = /6 + k/3, k Z, x = /2 + m, m Z.
| Na | k = 1 i m = 0 k = 4 i m = 1. |
seriale są takie same. |
3. Redukcja do jednorodności. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 3 sinx cosx + 6 cos 2 x = 5. ODZ: x – dowolne.
5 grzech 2 x + 3 sinx cosx + 6cos 2 x – 5 grzech 2 x – 5 cos 2 x = 0
3 sinxcosx + cos 2 x = 0 (1) nie można podzielić przez cos 2 x, ponieważ tracimy pierwiastki.
cos 2 x = 0 spełnia równanie.
cosx (3 sinx + cosx) = 0
cosx = 0. 3 sinx + cosx = 0.
x = /2 + k, k Z. tgx = –1/3, x = –/6 + n, n Z.
Odpowiedź: x = /2 + k, k Z. , x = –/6 + n, n Z
4. Równanie postaci: A(sinx + cosx) + B sin2x + C = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. O.D.Z.: x – dowolne.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | <
2
2 t 2 – 5 t + 2 = 0. t 1 = 2, t 2 = S.
sinx + cosx = S. cosx = grzech(x + /2),
sinx + grzech(x + /2) = 1/2,
2sin(x + /4) cos(–/4) = 1/2
grzech(x + /4) = 1/22;
x +/4 = (–1) k arcsin(1/2 O 2) + k, k Z.
Odpowiedź: x = (–1) k arcsin(1/22) – /4 + k, k Z.
5. Faktoryzacja.
1) cos 2 x – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2)(cosx + 2 sinx) = 0.
1) cosx = 2, bez pierwiastków.
2) cosx + 2 sinx = 0
2tgx + 1 = 0
Odpowiedź: x = arctan(1/2) + n, n Z.
III. Problemy pojawiające się przy rozwiązywaniu równań trygonometrycznych
1. Utrata pierwiastków: podziel przez g(x); Używamy niebezpiecznych formuł.
1) Znajdź błąd.
1 – cosx = sinx *sinx/2,
1 – cosx = 2sin 2 x/2 ze wzoru.
2 grzech 2 x/2 = 2 sinx/2* сosx/2* sinx/2 podzielić przez 2 grzech 2 x/2,
1 = cosx/2
x/2 = 2n, x = 4n, n" Z.
Utracone korzenie sinx/2 = 0, x = 2k, k Z.
Prawidłowe rozwiązanie: 2sin 2 x/2(1 – cosx/2) = 0.
| grzech 2x/2 = 0 x = 2k, k Z. |
1 – cosx /2 = 0 x = 4p n, n Z. |
2. Obce pierwiastki: pozbywamy się mianownika; podnieść do równej potęgi.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 3) = 0. O.D.Z.: sin2x 3 / 2.
2сos3х sinx – сos3x + 2sinx – 1 = 0
(cos3x + 1)(2sinx – 1) = 0
| 1). os3x + 1 = 0 x = /3 + 2n/3, n Z. |
2). 2sinx – 1 = 0 x = (–1) k /6 + k, k Z. |

| I. x = /3 + 2n/3 1. n = 0 grzech 2/3 = 3/2 nie zadowalaj. O.D.Z. 2. n = 1 3. n = 2 |
II. x = (–1) k /6 + k, k Z 1.k = 0 grzech 2/6 = 3/2 nie zadowalają O.D.Z. 2. k = 1 grzech 2*5/6 = –3 / 2 zadowolić O.D.Z. |
Odpowiedź: x = + 2k, x = 5/3 + 2k, x = 5/6 + 2k, k Z. t = 5 sin3x = 0
Podstawowe metody rozwiązywania równań
Jakie jest rozwiązanie równania?
Identyczna transformacja. Podstawowy
rodzaje transformacji tożsamości.
Korzeń obcy. Utrata korzeni.
Rozwiązanie równania jest procesem polegającym głównie na zastąpieniu danego równania innym równaniem mu równoważnym . To zastąpienie nazywa sięidentyczna transformacja . Główne przemiany tożsamości są następujące:
1.
Zastąpienie jednego wyrażenia innym, identycznie mu równym. Na przykład równanie (3 x+ 2 ) 2 = 15 x+ 10 można zastąpić następującym odpowiednikiem:9 X 2 + 12 x+ 4 = 15 x+ 10 .
2.
Przenoszenie składników równania z jednej strony na drugą za pomocą odwrotnych znaków. Zatem w poprzednim równaniu możemy przenieść wszystkie jego wyrazy z prawej strony na lewą ze znakiem „-”: 9 X 2 + 12 x+ 4 – 15 X - 10 = 0, po czym otrzymujemy:9 X 2 – 3 X - 6 = 0 .
3.
Mnożenie lub dzielenie obu stron równania przez to samo wyrażenie (liczbę) inne niż zero. Jest to bardzo ważne, ponieważnowe równanie może nie być równoważne poprzedniemu, jeśli wyrażenie, przez które mnożymy lub dzielimy, może być równe zero.
PRZYKŁAD RównanieX - 1 = 0 ma pojedynczy pierwiastekx = 1.
Mnożąc obie strony przezX - 3 , otrzymujemy równanie
( X - 1)( X - 3) = 0, co ma dwa pierwiastki:x = 1 iX = 3.
Ostatnia wartość nie jest pierwiastkiem danego równania
X - 1 = 0. Jest to tzwobcy korzeń .
I odwrotnie, podział może prowadzić doutrata korzeni . Więc
w naszym przypadku, jeśli (X - 1 )( X - 3 ) = 0 to oryginał
równanie, potem pierwiastekx = 3 zostaną utracone w dywizji
obie strony równaniaX - 3 .
W ostatnim równaniu (punkt 2) możemy podzielić wszystkie jego wyrazy przez 3 (a nie zero!) i ostatecznie otrzymać:
3 X 2 - X - 2 = 0 .
To równanie jest równoważne pierwotnemu:
(3 x+ 2) 2 = 15 x+ 10 .
4.
Mócpodnieś obie strony równania do nieparzystej potęgi Lubwyodrębnij pierwiastek nieparzysty z obu stron równania . Należy pamiętać, że:
a) budowa wnawet stopień może powodowaćdo nabycia obcych korzeni ;
B)zło ekstrakcjanawet root Może prowadzić doutrata korzeni .
PRZYKŁADY. Równanie 7X = 35 ma jeden korzeńX = 5 .
Podnosząc do kwadratu obie strony tego równania, otrzymujemy
równanie:
49 X 2 = 1225 .
mający dwa korzenie:X = 5 IX = – 5. Ostatnia wartość
jest obcym korzeniem.
Błędny biorąc pierwiastek kwadratowy z obu
części równania 49X 2 = 1225 wyników w 7X = 35,
i tracimy korzenieX = – 5.
Prawidłowy biorąc pierwiastek kwadratowy, otrzymasz wynik
równanie: | 7X | = 35, A stąd dwa przypadki:
1) 7 X = 35, NastępnieX = 5 ; 2) – 7 X = 35, NastępnieX = – 5 .
Dlatego kiedyprawidłowy wyodrębnianie kwadratu
pierwiastki nie tracimy pierwiastków równania.
Co znaczyPrawidłowy wyodrębnić korzeń? Tutaj się spotykamy
z bardzo ważną koncepcjąpierwiastek arytmetyczny
(cm. ).
Może prowadzić do pojawienia się tzw. korzeni obcych. W tym artykule najpierw szczegółowo przeanalizujemy, co to jest obce korzenie. Po drugie, porozmawiajmy o przyczynach ich wystąpienia. Po trzecie, na przykładach, rozważymy główne metody filtrowania obcych pierwiastków, to znaczy sprawdzania korzeni pod kątem obecności wśród nich obcych, aby wykluczyć je z odpowiedzi.
Zewnętrzne pierwiastki równania, definicja, przykłady
Podręczniki szkolne do algebry nie podają definicji pierwiastka zewnętrznego. Tam idea obcego pierwiastka powstaje poprzez opisanie następującej sytuacji: za pomocą niektórych przekształceń równania dokonuje się przejścia z równania pierwotnego do równania wtórnego, znajdują się pierwiastki powstałego równania uzupełniającego , a znalezione pierwiastki są sprawdzane poprzez podstawienie do pierwotnego równania, co pokazuje, że niektóre ze znalezionych pierwiastków nie są pierwiastkami pierwotnego równania, pierwiastki te nazywane są pierwiastkami obcymi pierwotnego równania.
Zaczynając od tej podstawy, możesz przyjąć dla siebie następującą definicję obcego korzenia:
Definicja
Obce korzenie są pierwiastkami równania wynikowego otrzymanego w wyniku przekształceń, które nie są pierwiastkami równania pierwotnego.
Podajmy przykład. Rozważmy równanie i konsekwencję tego równania x·(x−1)=0, otrzymaną przez zastąpienie wyrażenia identycznie równym wyrażeniem x·(x−1) . Oryginalne równanie ma pojedynczy pierwiastek 1. Równanie otrzymane w wyniku transformacji ma dwa pierwiastki 0 i 1. Oznacza to, że 0 jest obcym pierwiastkiem pierwotnego równania.
Przyczyny możliwego pojawienia się obcych korzeni
Jeśli do otrzymania równania wynikowego nie zastosujemy żadnych „egzotycznych” przekształceń, a jedynie podstawowe przekształcenia równań, to obce pierwiastki mogą powstać tylko z dwóch powodów:
- w związku z rozbudową ODZ i
- w wyniku podniesienia obu stron równania do tej samej potęgi.
Warto w tym miejscu przypomnieć, że ekspansja ODZ następuje głównie w wyniku przekształcenia równania
- Podczas redukcji ułamków;
- Zastępując produkt jednym lub większą liczbą współczynników zerowych przez zero;
- Zastępując ułamek licznikiem zerowym na zero;
- Podczas korzystania z niektórych właściwości potęg, pierwiastków, logarytmów;
- Podczas korzystania z niektórych wzorów trygonometrycznych;
- Kiedy obie strony równania zostaną pomnożone przez to samo wyrażenie, znika ono wraz z ODZ dla tego równania;
- Podczas uwalniania od znaków logarytmicznych w procesie rozwiązywania.
Przykład z poprzedniego akapitu artykułu ilustruje pojawienie się pierwiastka zewnętrznego na skutek rozwinięcia ODZ, które następuje przy przejściu od równania do równania wynikowego x·(x−1)=0. ODZ dla pierwotnego równania jest zbiorem wszystkich liczb rzeczywistych z wyjątkiem zera, ODZ dla wynikowego równania jest zbiorem R, to znaczy ODZ jest rozszerzany o liczbę zero. Liczba ta ostatecznie okazuje się obcym pierwiastkiem.
Podamy również przykład pojawienia się obcego pierwiastka w wyniku podniesienia obu stron równania do tej samej parzystej potęgi. Równanie irracjonalne ma pojedynczy pierwiastek 4, a konsekwencję tego równania uzyskaną z niego przez podniesienie obu stron równania do kwadratu, czyli równanie ![]() , ma dwa pierwiastki 1 i 4. Z tego jasno wynika, że podniesienie do kwadratu obu stron równania doprowadziło do pojawienia się zewnętrznego pierwiastka pierwotnego równania.
, ma dwa pierwiastki 1 i 4. Z tego jasno wynika, że podniesienie do kwadratu obu stron równania doprowadziło do pojawienia się zewnętrznego pierwiastka pierwotnego równania.
Należy zauważyć, że rozszerzenie ODZ i podniesienie obu stron równania do tej samej parzystej potęgi nie zawsze prowadzi do pojawienia się obcych pierwiastków. Na przykład, przechodząc od równania do równania wynikowego x=2, ODZ rozszerza się ze zbioru wszystkich liczb nieujemnych do zbioru wszystkich liczb rzeczywistych, ale nie pojawiają się żadne obce pierwiastki. 2 jest jedynym pierwiastkiem zarówno pierwszego, jak i drugiego równania. Ponadto przy przechodzeniu od równania do równania wynikowego nie pojawiają się żadne obce pierwiastki. Jedynym pierwiastkiem zarówno pierwszego, jak i drugiego równania jest x=16. Dlatego nie mówimy o przyczynach pojawienia się obcych korzeni, ale o przyczynach możliwego pojawienia się obcych korzeni.
Co to jest odsiewanie obcych korzeni?
Termin „odsiewanie obcych pierwiastków” można nazwać ustalonym jedynie z naciągnięciem; nie występuje on we wszystkich podręcznikach do algebry, ale jest intuicyjny i dlatego jest zwykle używany. Co oznacza odsiewanie obcych korzeni, staje się jasne z następującego wyrażenia: „... weryfikacja jest obowiązkowym krokiem w rozwiązaniu równania, które pomoże wykryć dodatkowe korzenie, jeśli takie istnieją, i odrzucić je (zwykle mówi się „wyeliminuj ”).”
Zatem,
Definicja
Odsiewanie obcych korzeni- jest to wykrywanie i odrzucanie obcych korzeni.
Teraz możesz przejść do metod odsiewania obcych korzeni.
Metody odsiewania obcych korzeni
Kontrola podmiany
Głównym sposobem odfiltrowania obcych korzeni jest test substytucji. Pozwala na wyeliminowanie obcych pierwiastków, które mogłyby powstać zarówno w wyniku ekspansji ODZ, jak i w wyniku podniesienia obu stron równania do tej samej parzystej potęgi.
Test podstawienia przebiega w następujący sposób: znalezione pierwiastki równania wynikowego podstawiamy kolejno do równania pierwotnego lub do dowolnego równania mu równoważnego, te, które dają poprawną równość liczbową, są pierwiastkami równania pierwotnego, a te, które dają niepoprawna równość liczbowa lub wyrażenie są pierwiastkami pierwotnego równania bez znaczenia, są obcymi pierwiastkami pierwotnego równania.
Pokażmy na przykładzie, jak odfiltrować obce pierwiastki poprzez podstawienie do pierwotnego równania.
W niektórych przypadkach bardziej celowe jest odfiltrowanie obcych korzeni innymi metodami. Dotyczy to głównie tych przypadków, gdy sprawdzanie przez podstawienie wiąże się ze znacznymi trudnościami obliczeniowymi lub gdy standardowa metoda rozwiązywania równań określonego typu wymaga innego sprawdzenia (na przykład odsiewanie obcych pierwiastków przy rozwiązywaniu ułamkowych równań wymiernych odbywa się zgodnie z zasadą warunkiem, że mianownik ułamka nie jest równy zero). Przyjrzyjmy się alternatywnym sposobom wyeliminowania obcych korzeni.
Według DL
W przeciwieństwie do testowania przez podstawienie, odfiltrowywanie obcych korzeni za pomocą ODZ nie zawsze jest właściwe. Faktem jest, że ta metoda pozwala odfiltrować tylko obce korzenie, które powstają w wyniku ekspansji ODZ i nie gwarantuje odsiewania obcych korzeni, które mogłyby powstać z innych powodów, na przykład z powodu podniesienia obu stron równania do tej samej parzystej potęgi. Co więcej, nie zawsze łatwo jest znaleźć OD dla rozwiązywanego równania. Niemniej jednak metoda odsiewania obcych korzeni za pomocą ODZ jest warta utrzymania w użyciu, ponieważ jej zastosowanie często wymaga mniej pracy obliczeniowej niż użycie innych metod.
Odsiewanie obcych pierwiastków zgodnie z ODZ przeprowadza się w następujący sposób: wszystkie znalezione pierwiastki równania wynikowego są sprawdzane, czy należą do zakresu dopuszczalnych wartości zmiennej dla pierwotnego równania lub dowolnego równania mu równoważnego, te, które należą do ODZ, są pierwiastkami pierwotnego równania, te, które należą do ODZ, są pierwiastkami pierwotnego równania, a te, które nie należą do ODZ, są obcymi pierwiastkami pierwotnego równania.
Analiza dostarczonych informacji prowadzi do wniosku, że wskazane jest odsianie obcych korzeni za pomocą ODZ, jeśli jednocześnie:
- łatwo jest znaleźć ODZ dla pierwotnego równania,
- obce korzenie mogły powstać jedynie w wyniku rozbudowy ODZ,
- Testowanie substytucji wiąże się ze znacznymi trudnościami obliczeniowymi.
Pokażemy, jak w praktyce odbywa się odchwaszczanie obcych korzeni.
Zgodnie z warunkami DL
Jak powiedzieliśmy w poprzednim akapicie, jeśli zewnętrzne pierwiastki mogłyby powstać tylko w wyniku ekspansji ODZ, wówczas można je wyeliminować, stosując ODZ do pierwotnego równania. Jednak nie zawsze łatwo jest znaleźć ODZ w postaci zbioru liczbowego. W takich przypadkach możliwe jest odsiewanie obcych korzeni nie według ODZ, ale zgodnie z warunkami określającymi ODZ. Wyjaśnijmy, jak odchwaszczanie obcych korzeni odbywa się w warunkach ODZ.
Znalezione pierwiastki są z kolei podstawiane pod warunki określające ODZ dla pierwotnego równania lub dowolnego równania mu równoważnego. Te, które spełniają wszystkie warunki, są pierwiastkami równania. A te z nich, które nie spełniają przynajmniej jednego warunku lub dają wyrażenie, które nie ma sensu, są obcymi pierwiastkami pierwotnego równania.
Podajmy przykład odsiewania obcych korzeni zgodnie z warunkami ODZ.
Wyeliminowanie obcych pierwiastków powstałych w wyniku podniesienia obu stron równania do parzystej potęgi
Oczywiste jest, że wyeliminowanie obcych pierwiastków powstałych w wyniku podniesienia obu stron równania do tej samej parzystej potęgi można dokonać poprzez podstawienie go do pierwotnego równania lub do dowolnego równoważnego mu równania. Jednak taka kontrola może wiązać się ze znacznymi trudnościami obliczeniowymi. W takim przypadku warto poznać alternatywną metodę odsiewania obcych korzeni, o której teraz porozmawiamy.
Odsiewanie obcych pierwiastków, które mogą powstać podczas podnoszenia obu stron irracjonalnych równań postaci do tej samej parzystej potęgi ![]() , gdzie n jest liczbą parzystą, można przeprowadzić zgodnie z warunkiem g(x)≥0. Wynika to z definicji pierwiastka stopnia parzystego: pierwiastkiem stopnia parzystego n jest liczbą nieujemną, której n-ta potęga jest równa liczbie pierwiastkowej, skąd
, gdzie n jest liczbą parzystą, można przeprowadzić zgodnie z warunkiem g(x)≥0. Wynika to z definicji pierwiastka stopnia parzystego: pierwiastkiem stopnia parzystego n jest liczbą nieujemną, której n-ta potęga jest równa liczbie pierwiastkowej, skąd  . Wyrażane podejście jest zatem swoistą symbiozą metody podnoszenia obu stron równania do tej samej potęgi i metody rozwiązywania równań niewymiernych poprzez wyznaczanie pierwiastka. Czyli równanie
. Wyrażane podejście jest zatem swoistą symbiozą metody podnoszenia obu stron równania do tej samej potęgi i metody rozwiązywania równań niewymiernych poprzez wyznaczanie pierwiastka. Czyli równanie ![]() , gdzie n jest liczbą parzystą, rozwiązuje się podnosząc obie strony równania do tej samej parzystej potęgi, a eliminując pierwiastki zewnętrzne, przeprowadza się zgodnie z warunkiem g(x)≥0, zaczerpniętym z metody rozwiązywania równań niewymiernych przez określenie korzenia.
, gdzie n jest liczbą parzystą, rozwiązuje się podnosząc obie strony równania do tej samej parzystej potęgi, a eliminując pierwiastki zewnętrzne, przeprowadza się zgodnie z warunkiem g(x)≥0, zaczerpniętym z metody rozwiązywania równań niewymiernych przez określenie korzenia.
Na ostatniej lekcji zastosowaliśmy trzy kroki do rozwiązania równań.
Pierwszy etap ma charakter techniczny. Korzystając z łańcucha przekształceń z pierwotnego równania, dochodzimy do dość prostego, które rozwiązujemy i znajdujemy pierwiastki.
Drugi etap to analiza rozwiązania. Analizujemy przekształcenia, które wykonaliśmy i sprawdzamy, czy są one równoważne.
Trzeci etap to weryfikacja. Sprawdzenie wszystkich znalezionych pierwiastków poprzez podstawienie ich do pierwotnego równania jest obowiązkowe przy wykonywaniu przekształceń, które mogą prowadzić do równania następstwa
Czy przy rozwiązywaniu równania zawsze konieczne jest rozróżnienie trzech etapów?
Oczywiście nie. Jak na przykład przy rozwiązywaniu tego równania. W życiu codziennym zazwyczaj nie są one rozróżniane. Ale o wszystkich tych etapach należy „pamiętać” i przeprowadzać je w takiej czy innej formie. Konieczne jest zbadanie równoważności przekształceń. A jeśli analiza wykaże, że należy przeprowadzić kontrolę, jest ona obowiązkowa. W przeciwnym razie równania nie można uznać za rozwiązane poprawnie.
Czy zawsze można sprawdzić pierwiastki równania tylko przez podstawienie?
Jeżeli przy rozwiązywaniu równania zastosowano przekształcenia równoważne, weryfikacja nie jest wymagana. Przy sprawdzaniu pierwiastków równania bardzo często stosuje się ODZ (dopuszczalny zakres wartości). Jeżeli sprawdzenie za pomocą ODZ jest trudne, wówczas dokonuje się tego poprzez podstawienie go do pierwotnego równania.
Ćwiczenie 1
Rozwiąż równanie pierwiastek kwadratowy z dwóch x plus trzy równa się jeden plus x.
Rozwiązanie
ODZ równania jest wyznaczany przez układ dwóch nierówności: dwa x plus trzy jest większe lub równe zero i jeden plus x jest większe lub równe zero. Rozwiązaniem jest x większe lub równe minus jeden.
Podnieśmy obie strony równania do kwadratu, przenieś wyrazy z jednej strony równania na drugą, dodaj podobne wyrazy i otrzymaj równanie kwadratowe x kwadrat równa się dwa. Jego korzenie są
x pierwszy, drugi równa się plus lub minus pierwiastek kwadratowy z dwóch.
Badanie
Wartość x pierwsza jest równa pierwiastkowi kwadratowemu z dwóch i jest pierwiastkiem równania, ponieważ jest uwzględniona w ODZ.
Wartość x sekundy równa się minus pierwiastek kwadratowy z dwóch nie jest pierwiastkiem równania, ponieważ nie jest on uwzględniony w DZ.
Sprawdźmy, czy pierwiastek x jest równy pierwiastkowi kwadratowemu z dwóch, podstawiając go do pierwotnej równości, otrzymamy
równość jest prawdziwa, co oznacza, że x równa się pierwiastkowi kwadratowemu z dwóch, co jest pierwiastkiem równania.
Odpowiedź: pierwiastek kwadratowy z dwóch.
Zadanie 2
Rozwiąż równanie pierwiastek kwadratowy z x minus osiem równa się pięć minus x.
Rozwiązanie
ODZ równania irracjonalnego jest wyznaczana przez układ dwóch nierówności: x minus osiem jest większe lub równe zero i pięć minus x jest większe lub równe zero. Rozwiązując go, okazuje się, że ten układ nie ma rozwiązań. Pierwiastkiem równania nie może być żadna z wartości zmiennej x.
Odpowiedź: brak korzeni.
Zadanie 3
Rozwiąż równanie pierwiastek kwadratowy z x do sześcianu plus cztery x minus jeden minus osiem pierwiastków kwadratowych x do potęgi czwartej minus x równa się pierwiastek kwadratowy z x do sześcianu minus jeden plus dwa pierwiastki kwadratowe z x.
Rozwiązanie
Znalezienie ODZ w tym równaniu jest dość trudne.
Przeprowadźmy transformację: podnieś obie strony tego równania do kwadratu,
Przesuńmy wszystkie wyrazy na lewą stronę równania i przyprowadźmy wyrazy podobne, napiszmy dwa pierwiastki pod jednym, otrzymamy podobne pierwiastki, przynieś podobne, podzielmy przez współczynnik minus 12 i uwzględnimy wyrażenie pierwiastkowe, otrzymamy równanie w postać iloczynu dwóch czynników równych zero. Po rozwiązaniu problemu znajdujemy korzenie:
x pierwsze jest równe jeden, x drugie jest równe zero.
Ponieważ podnieśliśmy obie strony równania do parzystej potęgi, sprawdzenie pierwiastków jest obowiązkowe.
Badanie
Jeśli x jest równe jeden, to
otrzymujemy poprawną równość, co oznacza, że x równa się jeden jest pierwiastkiem równania.

Jeśli x wynosi zero, to pierwiastek kwadratowy z minus jeden jest nieokreślony.
Oznacza to, że x równe zero jest obcym pierwiastkiem.
Odpowiedź: jedna.
Zadanie 4
Rozwiąż równanie logarytm wyrażenia x kwadrat plus pięć x plus dwa przy podstawie dwa równa się trzy.
Rozwiązanie
Znajdźmy równanie ODZ. Aby to zrobić, rozwiązujemy nierówność x kwadrat plus pięć x plus dwa przez zero.
Nierówność rozwiązujemy metodą przedziałową. Aby to zrobić, rozkładamy na czynniki jego lewą stronę, po wcześniejszym rozwiązaniu równania kwadratowego i biorąc pod uwagę znak nierówności, określamy ODZ. ODZ jest równy sumie promieni otwartych od minus nieskończoności do minus ułamka pięć plus pierwiastek kwadratowy z siedemnaście podzielony przez dwa i od minus ułamek pięć minus pierwiastek kwadratowy z siedemnaście podzielony przez dwa do plus nieskończoność.
Teraz zacznijmy znajdować pierwiastki równania. Biorąc pod uwagę, że trzy jest równe logarytmowi ośmiu do podstawy dwa, zapisujemy równanie w następujący sposób: logarytm wyrażenia x kwadrat plus pięć x plus dwa do podstawy dwa jest równy logarytmowi ośmiu do podstawy dwa. Wzmocnijmy równanie, otrzymajmy i rozwiążmy równanie kwadratowe.
Wyróżnikiem jest czterdzieści dziewięć.
Oblicz pierwiastki:
X pierwsze jest równe minus sześć; x sekunda równa się jeden.
Badanie
Minus sześć należy do ODZ, jeden należy do ODZ, co oznacza, że obie liczby są pierwiastkami równania.
Odpowiedź: minus sześć; jeden.
Na ostatniej lekcji przyjrzeliśmy się kwestii pojawiania się obcych korzeni. Możemy je wykryć poprzez weryfikację. Czy można stracić korzenie przy rozwiązywaniu równania i jak temu zapobiec?
Wykonując takie działania na równaniu, jak po pierwsze, dzieląc obie strony równania tym samym wyrażeniem ax od x (z wyjątkiem przypadków, gdy wiadomo na pewno, że ax od x nie jest równy zero dla dowolnego x od dziedzina definicji równania);
po drugie, zawężanie OD równania podczas procesu rozwiązywania może prowadzić do utraty pierwiastków równania.
Pamiętać!

Równanie zapisane jako
ef od x pomnożony przez popiół z x jest równy zhe od x pomnożony przez popiół z x rozwiązuje się w ten sposób:
musisz dokonać rozkładu na czynniki, umieszczając wspólny czynnik w nawiasach;
następnie przyrównaj każdy czynnik do zera, uzyskując w ten sposób dwa równania.
Obliczamy ich pierwiastki.
Ćwiczenie 1
Rozwiąż równanie x sześcian równa się x.
Pierwszy sposób
Dzielimy obie strony tego równania przez x, otrzymujemy x kwadrat równa się jeden, mając pierwiastek x pierwszy równa się jeden,
x sekunda równa się minus jeden.
Drugi sposób
X sześcian równa się X. Przesuńmy x na lewą stronę równania, usuńmy x z nawiasów i otrzymamy: x pomnożone przez x kwadrat minus jeden równa się zero.
Obliczmy jego pierwiastki:
X pierwsze jest równe zero, x drugie jest równe jeden, x trzecie jest równe minus jeden.
Równanie ma trzy pierwiastki.
Rozwiązując pierwszą metodę straciliśmy jeden pierwiastek - x równa się zero.
Odpowiedź: minus jeden; zero; jeden.
Pamiętać! Zmniejszenie obu stron równania o czynnik zawierający niewiadomą może spowodować utratę pierwiastków.
Zadanie 2
Rozwiąż równanie: logarytm dziesiętny x kwadrat jest równy dwa.
Rozwiązanie
Pierwszy sposób
Z definicji logarytmu otrzymujemy równanie kwadratowe x kwadrat równa się sto.
Jego pierwiastki: x pierwszy równa się dziesięć; X sekunda równa się minus dziesięć.
Drugi sposób
Z własności logarytmów wynika, że mamy dwa logarytmy dziesiętne x równa się dwa.
Jego pierwiastek - x jest równy dziesięć

W przypadku drugiej metody pierwiastek x równy minus dziesięć został utracony. A powodem jest to, że zastosowali złą formułę, zawężając zakres równania. Wyrażenie logarytmu dziesiętnego x kwadrat jest zdefiniowane dla wszystkich x z wyjątkiem x równego zero. Wyrażenie logarytmu dziesiętnego x jest takie, że x jest większe od zera. Prawidłowy wzór na logarytm dziesiętny x kwadrat jest równy modułowi dwóch logarytmów dziesiętnych x.
Pamiętać! Rozwiązując równanie, mądrze korzystaj z dostępnych wzorów.
Utrata pierwiastków i pierwiastków obcych podczas rozwiązywania równań
Miejska placówka oświatowa „Szkoła średnia nr 2 z pogłębioną nauką poszczególnych przedmiotów” w mieście Wsiewołożsk. Pracę badawczą przygotował uczeń klasy 11 B: Wasiliew Wasilij. Kierownik projektu: Egorova Ludmiła Aleksiejewna.
Równanie Najpierw przyjrzyjmy się różnym sposobom rozwiązania tego równania sinx+cosx =- 1
Rozwiązanie nr 1 sinx+cosx =-1 i Y x 0 1 sin(x+)=- 1 sin(x+)=- x+ =- +2 x+ = +2 + x=- +2 x= +2 Odpowiedź: + 2
Rozwiązanie nr 2 sinx+cosx =- Pierwsza odpowiedź: +2 y x 0 1 2sin cos + - + + = 0 sin cos + = 0 cos (cos + sin)= 0 cos =0 cos + sin =1 = + m tg =-1 = + m =- + x=- +2 x= +2
Rozwiązanie nr 3 I y x 0 1 sinx+cosx =- 1 2 = x= x+ x sin2x=0 2x= x= Odpowiedź:
sinx+cosx =-1 Rozwiązanie nr 4 i y x 0 1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n Odpowiedź: - + 2 n
Porównajmy rozwiązania Prawidłowe rozwiązania Zastanówmy się, w jakich przypadkach mogą pojawić się obce korzenie i dlaczego nr 2 Odpowiedź: +2 Nie. 3 Odpowiedź: Nie. 4 Odpowiedź: + 2 n Nie. 1 Odpowiedź: +2
Sprawdzanie rozwiązania Czy konieczne jest sprawdzanie? Sprawdź korzenie na wszelki wypadek, dla pewności? Jest to oczywiście przydatne, gdy łatwo je zastąpić, ale matematycy są ludźmi racjonalnymi i nie robią niepotrzebnych rzeczy. Przyjrzyjmy się różnym przypadkom i pamiętajmy, kiedy weryfikacja jest naprawdę potrzebna.
1. Najprostsze gotowe wzory c osx =a x=a =a s inx =a t gx =a W przypadkach, gdy pierwiastki znajdują się za pomocą najprostszych, gotowych wzorów, sprawdzanie nie jest konieczne. Korzystając jednak z takich formuł, należy pamiętać o warunkach, w jakich można je stosować. Na przykład wzór = można zastosować pod warunkiem a 0, -4ac 0. Odpowiedź x= arccos2+2 dla równania cosx =2 uważa się za duży błąd, ponieważ wzór x= arccos a +2 można przyjąć tylko używane do pierwiastków równania cosx =a, gdzie | | 1
2. Przekształcenia Częściej przy rozwiązywaniu równań trzeba przeprowadzić wiele przekształceń. Jeśli równanie zostanie zastąpione nowym, które ma wszystkie pierwiastki poprzedniego i zostanie przekształcone w taki sposób, że nie nastąpi utrata lub nabycie pierwiastków, wówczas takie równania nazywamy równoważnymi. 1. Podczas przenoszenia składników równania z jednej części do drugiej. 2. Podczas dodawania tej samej liczby do obu stron. 3. Gdy obie strony równania zostaną pomnożone przez tę samą liczbę niezerową. 4. Podczas stosowania tożsamości, które są prawdziwe na zbiorze wszystkich liczb rzeczywistych. Weryfikacja nie jest jednak wymagana!
Jednak nie każde równanie można rozwiązać za pomocą równoważnych przekształceń. Częściej konieczne jest zastosowanie przekształceń nierównych. Często takie przekształcenia opierają się na zastosowaniu formuł, które nie obowiązują dla wszystkich wartości rzeczywistych. Szczególnie w tym przypadku zmienia się dziedzina definicji równania. Ten błąd można znaleźć w rozwiązaniu nr 4. Przyjrzyjmy się błędowi, ale najpierw spójrzmy jeszcze raz na rozwiązanie nr 4. sinx+cosx=-1 + =-1 2tg +1- =-1- 2tg =-2 =- + n x = - + 2 n Błąd tkwi we wzorze sin2x= Można skorzystać z tego wzoru, ale należy dodatkowo sprawdzić czy pierwiastki są liczbami postaci +, dla których tg nie jest zdefiniowane. Teraz jest jasne, że rozwiązaniem jest utrata korzeni. Zobaczmy to do końca.
Rozwiązanie nr 4 i y x 0 1 Sprawdźmy liczby = + n przez podstawienie: x= + 2 n sin(+ 2 n)+ cos (+ 2 n)=sin + cos =0+(-1)=- 1 Zatem x= +2 n jest pierwiastkiem równania Odpowiedź: +2 sinx+cosx =-1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n
Przyjrzeliśmy się jednemu ze sposobów utraty korzeni; w matematyce jest ich bardzo wiele, więc trzeba je rozwiązywać ostrożnie, pamiętając o wszystkich zasadach. Tak jak możesz stracić pierwiastki równania, tak też możesz zdobyć dodatkowe w trakcie jego rozwiązywania. Rozważmy rozwiązanie nr 3, w którym popełniono taki błąd.
Rozwiązanie nr 3 I y x 0 1 2 2 i dodatkowe pierwiastki! Gdy obie strony równania zostaną podniesione do kwadratu, mogą pojawić się obce pierwiastki. W takim przypadku konieczne jest sprawdzenie. Dla n=2k mamy sin k+cos k=-1; cos k=-1 dla k=2m-1 , Wtedy n=2(2m+1)=4m+2 , x= = +2 m , Odpowiedź: +2 Dla n=2k+1 mamy sin +cos =- 1 sin(+ k)+ cos (+ k)=- 1 cos k-sin k=- 1 cos k=-1 gdzie k=2m+1 n=2(2m+1)+ 1=2m+3 x= ( 4m+3)= +2 m=- +2 sinx+cosx =- 1 = x= x+ x sin2x=0 2x= x=
Przyjrzeliśmy się zatem kilku możliwym przypadkom, a jest ich bardzo wiele. Staraj się nie marnować czasu i nie popełniać głupich błędów.
 Biografia Manikhasa Georgy'ego Moiseevicha
Biografia Manikhasa Georgy'ego Moiseevicha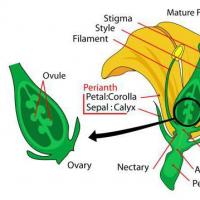 Botanika to dziedzina nauki o roślinach
Botanika to dziedzina nauki o roślinach Najskuteczniejsza poranna medytacja, wskazówki jak medytować o poranku
Najskuteczniejsza poranna medytacja, wskazówki jak medytować o poranku W jaki sposób wykorzystywana jest woda z siedmiu kościołów?
W jaki sposób wykorzystywana jest woda z siedmiu kościołów? Usuwanie szkód w kościele: moc Pana wybawi cię od silnego przekleństwa
Usuwanie szkód w kościele: moc Pana wybawi cię od silnego przekleństwa Jak usunąć z siebie negatywność w domu: skuteczne sposoby
Jak usunąć z siebie negatywność w domu: skuteczne sposoby