Cili transformim nuk çon në humbjen e rrënjëve. Transformimi i ekuacioneve, transformimet ekuivalente. Sipas kushteve të DL
Tema e ekuacioneve trigonometrike fillon me një leksion shkollor, i cili është strukturuar në formën e një bashkëbisedimi heuristik. Leksioni diskuton materialin teorik dhe shembuj të zgjidhjes së të gjitha problemeve tipike sipas planit:
- Ekuacionet më të thjeshta trigonometrike.
- Metodat themelore për zgjidhjen e ekuacioneve trigonometrike.
- Ekuacionet homogjene.
Në orët e mëposhtme fillon zhvillimi i pavarur i aftësive, bazuar në zbatimin e parimit të veprimtarisë së përbashkët mes mësuesit dhe nxënësit. Së pari, për studentët vendosen synimet, d.m.th. përcaktohet se kush nuk dëshiron të dijë më shumë se çfarë kërkohet nga standardi shtetëror dhe kush është i gatshëm të bëjë më shumë.
Diagnoza përfundimtare krijohet duke marrë parasysh diferencimin e nivelit, i cili u lejon studentëve të përcaktojnë me vetëdije njohuritë minimale që janë të nevojshme për të marrë notën "3". Bazuar në këtë, zgjidhen materiale shumë nivele për të diagnostikuar njohuritë e studentëve. Një punë e tillë lejon një qasje individuale ndaj studentëve, duke përfshirë të gjithë në aktivitetet e të mësuarit të ndërgjegjshëm, zhvillimin e aftësive të vetëorganizimit dhe të vetë-mësimit dhe sigurimin e një kalimi në të menduarit aktiv dhe të pavarur.
Seminari zhvillohet pas ushtrimit të aftësive bazë të zgjidhjes së ekuacioneve trigonometrike. Disa orë para seminarit, studentëve u jepen pyetje që do të diskutohen gjatë seminarit.
Seminari përbëhet nga tre pjesë.
1. Pjesa hyrëse mbulon të gjithë materialin teorik, duke përfshirë një hyrje në problemet që do të dalin gjatë zgjidhjes së ekuacioneve komplekse.
2. Pjesa e dytë diskuton zgjidhjen e ekuacioneve të formës:
- dhe cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- ekuacione të zgjidhshme duke ulur shkallën.
Këto ekuacione përdorin zëvendësimin universal, formulat e reduktimit të shkallës dhe metodën e argumentit ndihmës.
3. Pjesa e tretë trajton problemet e humbjes së rrënjëve dhe përvetësimin e rrënjëve të jashtme. Tregon se si të zgjidhni rrënjët.
Nxënësit punojnë në grupe. Për të zgjidhur shembujt, thirren djem të trajnuar mirë, të cilët mund të tregojnë dhe shpjegojnë materialin.
Seminari është projektuar për një student të përgatitur mirë, sepse... ai trajton çështje disi përtej qëllimit të materialit programor. Ai përfshin ekuacione të një forme më komplekse dhe trajton veçanërisht problemet që hasen në zgjidhjen e ekuacioneve komplekse trigonometrike.
Seminari u mbajt për nxënësit e klasave 10-11. Secili nxënës pati mundësinë të zgjeronte dhe thellonte njohuritë e tij mbi këtë temë, të krahasonte nivelin e njohurive të tij jo vetëm me kërkesat për një maturant, por edhe me kërkesat për ata që hyjnë në V.U.Z.
SEMINAR
Tema:"Zgjidhja e ekuacioneve trigonometrike"
Qëllimet:
- Përgjithësoni njohuritë për zgjidhjen e ekuacioneve trigonometrike të të gjitha llojeve.
- Fokusimi në problemet: humbja e rrënjëve; rrënjët e jashtme; përzgjedhja e rrënjës.
GJATË KLASËVE.
I. Pjesa hyrëse
1. Metodat bazë për zgjidhjen e ekuacioneve trigonometrike
- Faktorizimi.
- Prezantimi i një ndryshoreje të re.
- Metoda funksionale-grafike.
2. Disa lloje ekuacionesh trigonometrike.
- Ekuacione që reduktohen në ekuacione kuadratike në lidhje me cos x = t, sin x = t.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Bsinx + C = 0.
Ato zgjidhen duke futur një ndryshore të re.
- Ekuacione homogjene të shkallës së parë dhe të dytë
Ekuacioni i shkallës së parë: Asinx + Bcosx = 0 pjesëtojeni me cos x, marrim Atg x + B = 0
Ekuacioni i shkallës së dytë: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 pjesëtojeni me cos 2 x, marrim Atg 2 x + Btgx + C = 0
Ato zgjidhen me faktorizim dhe duke futur një ndryshore të re.
Të gjitha metodat zbatohen.
- Ulje:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Zgjidhet me metodën e faktorizimit.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Ekuacioni i formës: A(sinx + cosx) + Bsin2x + C = 0.
Reduktuar në katror në lidhje me t = sinx + cosx; sin2x = t 2 – 1.
3. Formulat.
x + 2n; Kërkohet kontroll!
- Fuqia në rënie: cos 2 x = (1 + cos2x): 2; sin 2 x = (1 – cos 2x): 2
- Metoda e argumentit ndihmës.
Le të zëvendësojmë Acosx + Bsinx me Csin (x + ), ku sin = a/C; cos=v/c;
– argument ndihmës.
4. Rregullat.
- Nëse shihni një katror, uleni shkallën.
- Nëse shihni një copë, bëni një sasi.
- Nëse e shihni shumën, bëni punën.
5. Humbja e rrënjëve, rrënjët shtesë.
- Humbja e rrënjëve: pjesëto me g(x); formula të rrezikshme (zëvendësim universal). Me këto operacione ne ngushtojmë fushën e përkufizimit.
- Rrënjët e tepërta: të ngritura në një fuqi të barabartë; shumëzohet me g(x) (liro emëruesin). Me këto operacione ne zgjerojmë fushën e përkufizimit.
II. Shembuj të ekuacioneve trigonometrike
1. Ekuacionet e formës Asinx + Bcosx = C
1) Zëvendësimi universal.O.D.Z. x – çdo.
3 sin 2x + cos 2x + 1= 0.
tgx = u. x/2 + n;
![]() u = – 1/3.
u = – 1/3.
tan x = –1/3, x = arctan (–1/3) + k, k Z.
Ekzaminimi: 3sin( + 2n) + cos( + 2n) + 1= 3 sin + cos + 1 = 0 – 1 + 1 = 0.
x = /2 + n, n e Z. Është rrënja e ekuacionit.
Përgjigje: x = arctan(–1/3) + k, k Z. x = /2 + n, n Z.
2) Metoda grafike funksionale. O.D.Z. x – çdo.
Sinx – cosx = 1
Sinx = cosx + 1.
Le të vizatojmë funksionet: y = sinx, y = cosx + 1.

Përgjigje: x = /2 + 2 n, Z; x = + 2k, k Z.
3) Paraqitja e një argumenti ndihmës. O.D.Z.: x – ndonjë.
8cosx + 15 sinx = 17.
![]()
8/17 cosx + 15/17 sinx = 1, sepse (8/17) 2 + (15/17) 2 = 1, atëherë ekziston i tillë që mëkati = 8/17,
cos = 15/17, që do të thotë mëkat cosx + sinx cos = 1; = harku 8/17.
Përgjigje: x = /2 + 2n – , x = /2 + 2n – hark 8/17, n Z.
2. Reduktimi i rendit: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). mëkat 2 3x + mëkat 2 4x + mëkat 2 6x + mëkat 2 7x = 2. O.D.Z.: x – ndonjë.
1 – cos 6x + 1 – cos 8x + 1 – cos 12x + 1 – cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x(cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Përgjigje: x = /20 + n/10, n Z. x = /6 + k/3, k Z, x = /2 + m, m Z.
| Në | k = 1 dhe m = 0 k = 4 dhe m = 1. |
seritë janë të njëjta. |
3. Reduktimi në homogjenitet. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 3 sinx cosx + 6 cos 2 x = 5. ODZ: x – çdo.
5 sin 2 x + 3 sinx cosx + 6cos 2 x – 5 sin 2 x – 5 cos 2 x = 0
3 sinxcosx + cos 2 x = 0 (1) nuk mund të pjesëtohet me cos 2 x, pasi humbasim rrënjët.
cos 2 x = 0 plotëson ekuacionin.
cosx (3 sinx + cosx) = 0
cosx = 0. 3 sinx + cosx = 0.
x = /2 + k, k Z. tgx = –1/3, x = –/6 + n, n Z.
Përgjigje: x = /2 + k, k Z. , x = –/6 + n, n Z
4. Ekuacioni i formës: A(sinx + cosx) + B sin2x + C = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. O.D.Z.: x – çdo.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | <
2
2 t 2 – 5t + 2 = 0. t 1 = 2, t 2 = S.
sinx + cosx = S. cosx = mëkat (x + /2),
sinx +sin(x + /2) = 1/2,
2sin(x + /4) cos(–/4) = 1/2
sin(x + /4) = 1/22;
x +/4 = (–1) k arcsin(1/2 O 2) + k, k Z.
Përgjigje: x = (–1) k hark (1/22) – /4 + k, k Z.
5. Faktorizimi.
1) cos 2 x – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2)(cosx + 2 sinx) = 0.
1) cosx = 2, pa rrënjë.
2) cosx + 2 sinx = 0
2tgx + 1 = 0
Përgjigje: x = arctan(1/2) + n, n Z.
III. Problemet që dalin gjatë zgjidhjes së ekuacioneve trigonometrike
1. Humbja e rrënjëve: pjesëto me g(x); Ne përdorim formula të rrezikshme.
1) Gjeni gabimin.
1 – cosx = sinx *sinx/2,
1 – formula cosx = 2sin 2 x/2.
2 mëkat 2 x/2 = 2 sinx/2* сosx/2* sinx/2 pjesëto me 2 mëkat 2 x/2,
1 = cosx/2
x/2 = 2n, x = 4n, n" Z.
Rrënjët e humbura sinx/2 = 0, x = 2k, k Z.
Zgjidhja e duhur: 2sin 2 x/2(1 – cosx/2) = 0.
| mëkat 2 x/2 = 0 x = 2k, k Z. |
1 – cosx /2 = 0 x = 4p n, n Z. |
2. Rrënjët e huaja: heqim qafe emëruesin; ngrihet në një fuqi të barabartë.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 3) = 0. O.D.Z.: sin2x 3 / 2.
2cos3x sinx – cos3x + 2sinx – 1 = 0
(cos3x + 1) (2sinx – 1) = 0
| 1). сos3x + 1 = 0 x = /3 + 2n/3, n Z. |
2). 2sinx – 1 = 0 x = (–1) k /6 + k, k Z. |

| I. x = /3 + 2n/3 1. n = 0 mëkati 2/3 = 3/2 nuk kënaq. O.D.Z. 2. n = 1 3. n = 2 |
II. x = (–1) k /6 + k, k Z 1.k = 0 mëkati 2/6 = 3/2 nuk e kënaqin O.D.Z. 2. k = 1 mëkati 2*5/6 = –3/2 kënaq O.D.Z. |
Përgjigje: x = + 2k, x = 5/3 + 2k, x = 5/6 + 2k, k Z. t = 5 sin3x = 0
Metodat themelore për zgjidhjen e ekuacioneve
Cila është zgjidhja e një ekuacioni?
Transformim identik. bazë
llojet e transformimeve të identitetit.
Rrënjë e huaj. Humbja e rrënjës.
Zgjidhja e ekuacionit është një proces që konsiston kryesisht në zëvendësimin e një ekuacioni të dhënë me një ekuacion tjetër që është ekuivalent me të . Ky zëvendësim quhettransformim identik . Transformimet kryesore të identitetit janë si më poshtë:
1.
Zëvendësimi i një shprehjeje me një tjetër që është identikisht e barabartë me të. Për shembull, ekuacioni (3 x+ 2 ) 2 = 15 x+ 10 mund të zëvendësohet me ekuivalentin e mëposhtëm:9 x 2 + 12 x+ 4 = 15 x+ 10 .
2.
Transferimi i termave të një ekuacioni nga njëra anë në tjetrën me shenja të kundërta. Pra, në ekuacionin e mëparshëm mund t'i transferojmë të gjithë termat e tij nga ana e djathtë në të majtë me shenjën "-": 9 x 2 + 12 x+ 4 – 15 x - 10 = 0, pas së cilës marrim:9 x 2 – 3 x - 6 = 0 .
3.
Shumëzimi ose pjesëtimi i të dy anëve të një ekuacioni me të njëjtën shprehje (numër) përveç zeros. Kjo është shumë e rëndësishme sepseekuacioni i ri mund të mos jetë i barabartë me atë të mëparshëm nëse shprehja me të cilën po shumëzojmë ose pjesëtojmë mund të jetë e barabartë me zero.
SHEMBULL Ekuacionix - 1 = 0 ka një rrënjë të vetmex = 1.
Duke shumëzuar të dyja anët mex - 3 , marrim ekuacionin
( x - 1)( x - 3) = 0, e cila ka dy rrënjë:x = 1 dhex = 3.
Vlera e fundit nuk është rrënja e ekuacionit të dhënë
x - 1 = 0. Ky është i ashtuquajturirrënjë e jashtme .
Në të kundërt, ndarja mund të çojë nëhumbja e rrënjës . Kështu që
në rastin tonë, nëse (x - 1 )( x - 3 ) = 0 është origjinali
ekuacioni, pastaj rrënjax = 3 do të humbasë në ndarje
të dyja anët e ekuacionit nëx - 3 .
Në ekuacionin e fundit (pika 2), ne mund t'i ndajmë të gjithë termat e tij me 3 (jo zero!) dhe në fund të marrim:
3 x 2 – x – 2 = 0 .
Ky ekuacion është i barabartë me atë origjinal:
(3 x+ 2) 2 = 15 x+ 10 .
4.
Mundngrini të dyja anët e ekuacionit në një fuqi tek osenxirrni rrënjën tek nga të dyja anët e ekuacionit . Është e nevojshme të mbani mend se:
a) ndërtimi nëmadje shkallë mund të shkaktojëpër marrjen e rrënjëve të huaja ;
b)gabim nxjerrjesedhe rrënjë mund të çojë nëhumbja e rrënjëve .
SHEMBUJ. Ekuacioni 7x = 35 ka një rrënjë të vetmex = 5 .
Duke kuadruar të dyja anët e këtij ekuacioni, marrim
ekuacioni:
49 x 2 = 1225 .
me dy rrënjë:x = 5 Dhex = – 5. Vlera e fundit
është një rrënjë e jashtme.
E pasaktë duke marrë rrënjën katrore të të dyjave
pjesë të ekuacionit 49x 2 = 1225 rezulton në 7x = 35,
dhe ne po humbasim rrënjët tonax = – 5.
E sakte marrja e rrënjës katrore rezulton në
ekuacioni: | 7x | = 35, A pra në dy raste:
1) 7 x = 35, Pastajx = 5 ; 2) – 7 x = 35, Pastajx = – 5 .
Prandaj, kurkorrekte nxjerrje katror
rrënjët nuk i humbim rrënjët e ekuacionit.
Qe do te thoteE drejta nxjerr rrënjën? Këtu takohemi
me një koncept shumë të rëndësishëmrrënjë aritmetike
(cm. ).
Mund të çojë në shfaqjen e të ashtuquajturave rrënjë të jashtme. Në këtë artikull, së pari do të analizojmë në detaje se çfarë është rrënjët e jashtme. Së dyti, le të flasim për arsyet e shfaqjes së tyre. Dhe së treti, duke përdorur shembuj, ne do të shqyrtojmë metodat kryesore të filtrimit të rrënjëve të jashtme, domethënë kontrollimin e rrënjëve për praninë e të huajve midis tyre, në mënyrë që t'i përjashtojmë ato nga përgjigja.
Rrënjët e jashtme të ekuacionit, përkufizimi, shembuj
Tekstet shkollore të algjebrës nuk japin një përkufizim të një rrënjeje të jashtme. Aty, ideja e një rrënje të jashtme formohet duke përshkruar situatën e mëposhtme: me ndihmën e disa transformimeve të ekuacionit, bëhet një kalim nga ekuacioni origjinal në ekuacionin pasues, gjenden rrënjët e ekuacionit rrjedhës që rezulton. , dhe rrënjët e gjetura kontrollohen duke zëvendësuar në ekuacionin origjinal, gjë që tregon se disa nga rrënjët e gjetura nuk janë rrënjë të ekuacionit origjinal, këto rrënjë quhen rrënjë të jashtme për ekuacionin origjinal.
Duke u nisur nga kjo bazë, ju mund të pranoni vetë përkufizimin e mëposhtëm të një rrënjë të huaj:
Përkufizimi
Rrënjët e huaja- këto janë rrënjët e ekuacionit përfundues të marrë si rezultat i shndërrimeve, të cilat nuk janë rrënjët e ekuacionit origjinal.
Le të japim një shembull. Le të shqyrtojmë ekuacionin dhe pasojën e këtij ekuacioni x·(x−1)=0, të marra duke zëvendësuar shprehjen me shprehjen identike të barabartë x·(x−1) . Ekuacioni origjinal ka një rrënjë të vetme 1. Ekuacioni i marrë si rezultat i transformimit ka dy rrënjë 0 dhe 1. Kjo do të thotë se 0 është një rrënjë e jashtme për ekuacionin origjinal.
Arsyet për shfaqjen e mundshme të rrënjëve të huaja
Nëse për të marrë ekuacionin pasardhës nuk përdorni ndonjë transformim "ekzotik", por përdorni vetëm transformime bazë të ekuacioneve, atëherë rrënjët e jashtme mund të lindin vetëm për dy arsye:
- për shkak të zgjerimit të ODZ dhe
- për shkak të ngritjes së të dy anëve të ekuacionit në të njëjtën fuqi çift.
Vlen të kujtojmë këtu se zgjerimi i ODZ si rezultat i transformimit të ekuacionit ndodh kryesisht
- Kur zvogëloni fraksionet;
- Kur zëvendësoni një produkt me një ose më shumë faktorë zero me zero;
- Kur një thyesë me një numërues zero zëvendësohet me zero;
- Kur përdoren disa veti të fuqive, rrënjëve, logaritmeve;
- Kur përdoren disa formula trigonometrike;
- Kur të dyja anët e një ekuacioni shumëzohen me të njëjtën shprehje, ajo zhduket me ODZ për atë ekuacion;
- Kur lirohet nga shenjat logaritmike në procesin e zgjidhjes.
Shembulli nga paragrafi i mëparshëm i artikullit ilustron shfaqjen e një rrënjeje të jashtme për shkak të zgjerimit të ODZ, i cili ndodh kur kalohet nga ekuacioni në ekuacionin pasardhës x·(x−1)=0. ODZ për ekuacionin origjinal është bashkësia e të gjithë numrave realë, me përjashtim të zeros, ODZ për ekuacionin që rezulton është bashkësia R, domethënë, ODZ zgjerohet me numrin zero. Ky numër përfundimisht rezulton të jetë një rrënjë e jashtme.
Do të japim gjithashtu një shembull të shfaqjes së një rrënjë të jashtme për shkak të ngritjes së të dy anëve të ekuacionit në të njëjtën fuqi çift. Ekuacioni irracional ka një rrënjë të vetme 4, dhe pasoja e këtij ekuacioni, e marrë prej saj duke katrorizuar të dy anët e ekuacionit, domethënë ekuacionin ![]() , ka dy rrënjë 1 dhe 4. Nga kjo është e qartë se kuadrimi i të dy anëve të ekuacionit çoi në shfaqjen e një rrënjë të jashtme për ekuacionin origjinal.
, ka dy rrënjë 1 dhe 4. Nga kjo është e qartë se kuadrimi i të dy anëve të ekuacionit çoi në shfaqjen e një rrënjë të jashtme për ekuacionin origjinal.
Vini re se zgjerimi i ODZ dhe ngritja e të dy anëve të ekuacionit në të njëjtën fuqi çift nuk çon gjithmonë në shfaqjen e rrënjëve të jashtme. Për shembull, kur lëvizim nga ekuacioni në ekuacionin pasardhës x=2, ODZ zgjerohet nga bashkësia e të gjithë numrave jonegativë në bashkësinë e të gjithë numrave realë, por nuk shfaqen rrënjë të jashtme. 2 është rrënja e vetme e ekuacionit të parë dhe të dytë. Gjithashtu, asnjë rrënjë e jashtme nuk shfaqet kur lëviz nga një ekuacion në një ekuacion pasardhës. Rrënja e vetme e barazimit të parë dhe të dytë është x=16. Kjo është arsyeja pse ne nuk po flasim për arsyet e shfaqjes së rrënjëve të jashtme, por për arsyet e shfaqjes së mundshme të rrënjëve të jashtme.
Çfarë është skanimi i rrënjëve të jashtme?
Termi "shoshitje e rrënjëve të jashtme" mund të quhet vetëm me një shtrirje, ai nuk gjendet në të gjitha tekstet shkollore të algjebrës, por është intuitiv, prandaj përdoret zakonisht. Çfarë nënkuptohet me shoshitjen e rrënjëve të jashtme bëhet e qartë nga fraza e mëposhtme: "... verifikimi është një hap i detyrueshëm në zgjidhjen e një ekuacioni, i cili do të ndihmojë për të zbuluar rrënjët e jashtme, nëse ka, dhe për t'i hedhur ato (zakonisht ata thonë "zhduk ”)”
Kështu,
Përkufizimi
Ekzaminimi i rrënjëve të jashtme- ky është zbulimi dhe hedhja e rrënjëve të jashtme.
Tani mund të kaloni në metodat e shqyrtimit të rrënjëve të jashtme.
Metodat për skanimin e rrënjëve të jashtme
Kontrolli i zëvendësimit
Mënyra kryesore për të filtruar rrënjët e jashtme është një test zëvendësimi. Kjo ju lejon të hiqni rrënjët e jashtme që mund të lindin si për shkak të zgjerimit të ODZ ashtu edhe për shkak të ngritjes së të dy anëve të ekuacionit në të njëjtën fuqi të barabartë.
Testi i zëvendësimit është si më poshtë: rrënjët e gjetura të ekuacionit konkluzion zëvendësohen nga ana e tyre në ekuacionin origjinal ose në ndonjë ekuacion ekuivalent me të, ato që japin barazinë numerike të saktë janë rrënjët e ekuacionit origjinal dhe ato që japin barazia ose shprehja e gabuar numerike janë rrënjët e ekuacionit origjinal të pakuptimta, janë rrënjë të jashtme për ekuacionin origjinal.
Le të tregojmë me një shembull se si të filtrohen rrënjët e jashtme përmes zëvendësimit në ekuacionin origjinal.
Në disa raste, është më e përshtatshme të filtroni rrënjët e jashtme duke përdorur metoda të tjera. Kjo vlen kryesisht për ato raste kur kontrolli me zëvendësim shoqërohet me vështirësi të konsiderueshme llogaritëse ose kur metoda standarde e zgjidhjes së ekuacioneve të një lloji të caktuar kërkon një kontroll tjetër (për shembull, shqyrtimi i rrënjëve të jashtme kur zgjidhja e ekuacioneve racionale të pjesshme kryhet sipas kusht që emëruesi i thyesës të mos jetë i barabartë me zero). Le të shohim mënyra alternative për të hequr rrënjët e jashtme.
Sipas DL
Ndryshe nga testimi me zëvendësim, filtrimi i rrënjëve të jashtme duke përdorur ODZ nuk është gjithmonë i përshtatshëm. Fakti është se kjo metodë ju lejon të filtroni vetëm rrënjët e jashtme që lindin për shkak të zgjerimit të ODZ, dhe nuk garanton shoshitjen e rrënjëve të jashtme që mund të lindin për arsye të tjera, për shembull, për shkak të ngritjes së të dy palëve. të ekuacionit për të njëjtën fuqi çift . Për më tepër, nuk është gjithmonë e lehtë të gjesh OD për ekuacionin që zgjidhet. Sidoqoftë, metoda e shoshitjes së rrënjëve të jashtme duke përdorur ODZ ia vlen të mbahet në shërbim, pasi përdorimi i saj shpesh kërkon më pak punë llogaritëse sesa përdorimi i metodave të tjera.
Heqja e rrënjëve të jashtme sipas ODZ kryhet si më poshtë: kontrollohen të gjitha rrënjët e gjetura të ekuacionit pasardhës për të parë nëse i përkasin diapazonit të vlerave të lejuara të ndryshores për ekuacionin origjinal ose ndonjë ekuacion të barabartë me të. ato që i përkasin ODZ-së janë rrënjë të ekuacionit origjinal, dhe ato që i përkasin ODZ-së janë rrënjë të ekuacionit origjinal, dhe ato që nuk i përkasin ODZ-së janë rrënjë të jashtme për ekuacionin origjinal.
Analiza e informacionit të dhënë çon në përfundimin se është e këshillueshme që të analizohen rrënjët e jashtme duke përdorur ODZ nëse në të njëjtën kohë:
- është e lehtë të gjesh ODZ për ekuacionin origjinal,
- rrënjët e jashtme mund të lindin vetëm për shkak të zgjerimit të ODZ,
- Testimi i zëvendësimit shoqërohet me vështirësi të konsiderueshme llogaritëse.
Ne do të tregojmë se si kryhet në praktikë heqja e rrënjëve të jashtme.
Sipas kushteve të DL
Siç thamë në paragrafin e mëparshëm, nëse rrënjët e jashtme mund të lindin vetëm për shkak të zgjerimit të ODZ, atëherë ato mund të eliminohen duke përdorur ODZ për ekuacionin origjinal. Por nuk është gjithmonë e lehtë të gjesh ODZ në formën e një grupi numerik. Në raste të tilla, është e mundur të ekzaminohen rrënjët e jashtme jo sipas ODZ, por sipas kushteve që përcaktojnë ODZ. Le të shpjegojmë se si kryhet heqja e rrënjëve të jashtme në kushtet e ODZ.
Rrënjët e gjetura zëvendësohen nga ana e tyre në kushtet që përcaktojnë ODZ për ekuacionin origjinal ose ndonjë ekuacion të barazvlefshëm me të. Ato që plotësojnë të gjitha kushtet janë rrënjët e ekuacionit. Dhe ato prej tyre që nuk plotësojnë të paktën një kusht ose japin një shprehje që nuk ka kuptim janë rrënjë të jashtme për ekuacionin origjinal.
Le të japim një shembull të skanimit të rrënjëve të jashtme sipas kushteve të ODZ.
Zhdukja e rrënjëve të jashtme që dalin nga ngritja e të dyja anëve të ekuacionit në një fuqi të barabartë
Është e qartë se heqja e rrënjëve të jashtme që dalin nga ngritja e të dyja anëve të ekuacionit në të njëjtën fuqi çift mund të bëhet duke e zëvendësuar atë në ekuacionin origjinal ose në ndonjë ekuacion të barabartë me të. Por një kontroll i tillë mund të përfshijë vështirësi të konsiderueshme llogaritëse. Në këtë rast, ia vlen të dini një metodë alternative për të shoshitur rrënjët e jashtme, për të cilën do të flasim tani.
Ekzaminimi i rrënjëve të jashtme që mund të lindin kur të dyja anët e ekuacioneve irracionale të formës ngrihen në të njëjtën fuqi të barabartë ![]() , ku n është një numër çift, mund të kryhet sipas kushtit g(x)≥0. Kjo rrjedh nga përkufizimi i rrënjës së një shkalle çift: një rrënjë e një shkalle çift n është një numër jo negativ, fuqia n e të cilit është e barabartë me numrin radikal, prej nga
, ku n është një numër çift, mund të kryhet sipas kushtit g(x)≥0. Kjo rrjedh nga përkufizimi i rrënjës së një shkalle çift: një rrënjë e një shkalle çift n është një numër jo negativ, fuqia n e të cilit është e barabartë me numrin radikal, prej nga  . Kështu, qasja e shprehur është një lloj simbiozë e metodës së ngritjes së të dy anëve të ekuacionit në të njëjtën fuqi dhe metodës së zgjidhjes së ekuacioneve irracionale duke përcaktuar rrënjën. Kjo është, ekuacioni
. Kështu, qasja e shprehur është një lloj simbiozë e metodës së ngritjes së të dy anëve të ekuacionit në të njëjtën fuqi dhe metodës së zgjidhjes së ekuacioneve irracionale duke përcaktuar rrënjën. Kjo është, ekuacioni ![]() , ku n është një numër çift, zgjidhet duke ngritur të dyja anët e ekuacionit në të njëjtën fuqi çift, dhe eliminimi i rrënjëve të jashtme kryhet sipas kushtit g(x)≥0, marrë nga metoda e zgjidhjes së ekuacioneve irracionale me përcaktimi i rrënjës.
, ku n është një numër çift, zgjidhet duke ngritur të dyja anët e ekuacionit në të njëjtën fuqi çift, dhe eliminimi i rrënjëve të jashtme kryhet sipas kushtit g(x)≥0, marrë nga metoda e zgjidhjes së ekuacioneve irracionale me përcaktimi i rrënjës.
Në mësimin e fundit, ne përdorëm tre hapa për të zgjidhur ekuacionet.
Faza e parë është teknike. Duke përdorur një zinxhir transformimesh nga ekuacioni origjinal, arrijmë në një ekuacion mjaft të thjeshtë, të cilin e zgjidhim dhe gjejmë rrënjët.
Faza e dytë është analiza e zgjidhjes. Ne analizojmë transformimet që kemi kryer dhe zbulojmë nëse ato janë ekuivalente.
Faza e tretë është verifikimi. Kontrollimi i të gjitha rrënjëve të gjetura duke i zëvendësuar ato në ekuacionin origjinal është i detyrueshëm kur kryhen transformime që mund të çojnë në një ekuacion përfundues
A është gjithmonë e nevojshme të dallohen tre faza gjatë zgjidhjes së një ekuacioni?
Sigurisht që jo. Si, për shembull, në zgjidhjen e këtij ekuacioni. Në jetën e përditshme zakonisht nuk dallohen. Por të gjitha këto faza duhet të "mbahen parasysh" dhe të kryhen në një formë ose në një tjetër. Është e domosdoshme të analizohet ekuivalenca e transformimeve. Dhe nëse analiza tregon se duhet kryer një kontroll, atëherë ai është i detyrueshëm. Përndryshe, ekuacioni nuk mund të konsiderohet i zgjidhur saktë.
A është gjithmonë e mundur të kontrollohen rrënjët e një ekuacioni vetëm me zëvendësim?
Nëse gjatë zgjidhjes së ekuacionit janë përdorur transformime ekuivalente, atëherë verifikimi nuk kërkohet. Kur kontrolloni rrënjët e një ekuacioni, përdoret shumë shpesh ODZ (vargu i vlerave të lejuara) Nëse është e vështirë të kontrollohet duke përdorur ODZ, atëherë ai kryhet duke e zëvendësuar atë në ekuacionin origjinal.
Ushtrimi 1
Zgjidheni ekuacionin rrënjë katrore e dy x plus tre është e barabartë me një plus x.
Zgjidhje
ODZ e ekuacionit përcaktohet nga një sistem i dy pabarazive: dy x plus tre është më i madh ose i barabartë me zero dhe një plus x është më i madh ose i barabartë me zero. Zgjidhja është x më e madhe ose e barabartë me minus një.
Le të vendosim në katror të dy anët e ekuacionit, të zhvendosim termat nga njëra anë e ekuacionit në tjetrën, të shtojmë terma të ngjashëm dhe të marrim një ekuacion kuadratik x në katror është i barabartë me dy. Rrënjët e saj janë
x e para, e dyta është e barabartë me plus ose minus rrënjën katrore të dy.
Ekzaminimi
Vlera e x së pari është e barabartë me rrënjën katrore të dy është rrënja e ekuacionit, pasi është përfshirë në ODZ.
Vlera e x sekondës është e barabartë me minus rrënja katrore e dy nuk është rrënja e ekuacionit, sepse nuk përfshihet në DZ.
Le të kontrollojmë se rrënja x është e barabartë me rrënjën katrore të dy, duke e zëvendësuar atë në barazinë origjinale, marrim
barazia është e vërtetë, që do të thotë se x është e barabartë me rrënjën katrore të dy është rrënja e ekuacionit.
Përgjigje: rrënja katrore e dy.
Detyra 2
Zgjidheni ekuacionin rrënja katrore e x minus tetë është e barabartë me pesë minus x.
Zgjidhje
ODZ e një ekuacioni irracional përcaktohet nga një sistem me dy pabarazi: x minus tetë është më i madh ose i barabartë me zero dhe pesë minus x është më i madh ose i barabartë me zero. Duke e zgjidhur atë, ne zbulojmë se ky sistem nuk ka zgjidhje. Rrënja e ekuacionit nuk mund të jetë asnjë nga vlerat e ndryshores x.
Përgjigje: pa rrënjë.
Detyra 3
Zgjidheni ekuacionin rrënja katrore e x kub plus katër x minus një minus tetë rrënjë katrore të x me fuqinë e katërt minus x është e barabartë me rrënjën katrore të x në kub minus një plus dy rrënjë katrore të x.
Zgjidhje
Gjetja e ODZ në këtë ekuacion është mjaft e vështirë.
Le të bëjmë transformimin: katrore të dy anët e këtij ekuacioni,
Le t'i zhvendosim të gjithë termat në anën e majtë të ekuacionit dhe të sjellim terma të ngjashëm, të shkruajmë dy rrënjë nën një, të marrim radikale të ngjashme, të sjellim të ngjashëm, të pjesëtojmë me koeficientin minus 12 dhe faktorizojmë shprehjen radikale, marrim një ekuacion në forma e prodhimit të dy faktorëve të barabartë me zero. Pasi e kemi zgjidhur, gjejmë rrënjët:
x e para është e barabartë me një, x e dyta është e barabartë me zero.
Meqenëse i ngritëm të dyja anët e ekuacionit në një fuqi të barabartë, kontrollimi i rrënjëve është i detyrueshëm.
Ekzaminimi
Nëse x është e barabartë me një, atëherë
marrim barazinë e saktë, që do të thotë se x është e barabartë me një është rrënja e ekuacionit.

Nëse x është zero, atëherë rrënja katrore e minus një është e papërcaktuar.
Kjo do të thotë se x e barabartë me zero është një rrënjë e jashtme.
Përgjigje: një.
Detyra 4
Të zgjidhet logaritmi i ekuacionit të shprehjes x në katror plus pesë x plus dy bazë dy është e barabartë me tre.
Zgjidhje
Le të gjejmë ekuacionin ODZ. Për ta bërë këtë, ne zgjidhim pabarazinë x në katror plus pesë x plus dy mbi zero.
Ne e zgjidhim pabarazinë duke përdorur metodën e intervalit. Për ta bërë këtë, ne faktorizojmë anën e majtë të saj, pasi kemi zgjidhur më parë ekuacionin kuadratik dhe duke marrë parasysh shenjën e pabarazisë, përcaktojmë ODZ. ODZ është e barabartë me bashkimin e rrezeve të hapura nga minus pafundësia në minus fraksioni pesë plus rrënjën katrore të shtatëmbëdhjetë pjesëtuar me dy, dhe nga minus fraksioni pesë minus rrënjën katrore të shtatëmbëdhjetë pjesëtuar me dy në plus pafundësi.
Tani le të fillojmë të gjejmë rrënjët e ekuacionit. Duke qenë se tre është e barabartë me logaritmin e tetë me bazën dy, e shkruajmë ekuacionin si më poshtë: logaritmi i shprehjes x katror plus pesë x plus dy me bazën dy është i barabartë me logaritmin e tetë me bazën dy. Le të fuqizojmë ekuacionin, të marrim dhe të zgjidhim një ekuacion kuadratik.
Diskriminuesi është dyzet e nëntë.
Llogaritni rrënjët:
X e para është e barabartë me minus gjashtë; x sekondë është e barabartë me një.
Ekzaminimi
Minus gjashtë i përket ODZ, një i përket ODZ, që do të thotë që të dy numrat janë rrënjët e ekuacionit.
Përgjigje: minus gjashtë; një.
Në mësimin e fundit, ne shqyrtuam çështjen e shfaqjes së rrënjëve të jashtme. Ne mund t'i zbulojmë ato përmes verifikimit. A është e mundur të humbni rrënjët kur zgjidhni një ekuacion dhe si ta parandaloni këtë?
Kur kryeni veprime të tilla në një ekuacion, si p.sh., së pari, pjesëtimi i të dy anëve të ekuacionit me të njëjtën shprehje ax nga x (përveç atyre rasteve kur dihet me siguri se boshti nga x nuk është i barabartë me zero për çdo x nga fusha e përkufizimit të ekuacionit);
së dyti, ngushtimi i OD të ekuacionit gjatë procesit të zgjidhjes mund të çojë në humbjen e rrënjëve të ekuacionit.
Mbani mend!

Ekuacioni i shkruar si
ef nga x e shumëzuar me hi nga x është e barabartë me zhe nga x e shumëzuar me hi nga x zgjidhet në këtë mënyrë:
ju duhet të faktorizoni duke e vendosur faktorin e përbashkët jashtë kllapave;
atëherë, barazoni çdo faktor me zero, duke marrë dy ekuacione.
Ne llogarisim rrënjët e tyre.
Ushtrimi 1
Zgjidheni ekuacionin x kubi është i barabartë me x.
Mënyra e parë
Le t'i ndajmë të dy anët e këtij ekuacioni me x, marrim x katror është i barabartë me një, duke pasur rrënjë x fillimisht është një,
x sekondë është e barabartë me minus një.
Mënyra e dytë
X kubi është i barabartë me X. Le të zhvendosim x në anën e majtë të ekuacionit, të marrim x nga kllapat dhe marrim: x shumëzuar me x në katror minus një është zero.
Le të llogarisim rrënjët e tij:
X e para është e barabartë me zero, x e dyta është e barabartë me një, x e treta është e barabartë me minus një.
Ekuacioni ka tre rrënjë.
Kur zgjidhëm metodën e parë, humbëm një rrënjë - x është zero.
Përgjigje: minus një; zero; një.
Mbani mend! Zvogëlimi i të dyja anëve të ekuacionit me një faktor që përmban të panjohurën mund të rezultojë në humbjen e rrënjëve.
Detyra 2
Zgjidheni ekuacionin: logaritmi dhjetor i x në katror është i barabartë me dy.
Zgjidhje
Mënyra e parë
Nga përkufizimi i një logaritmi, marrim ekuacionin kuadratik x katror është i barabartë me njëqind.
Rrënjët e saj: x së pari është dhjetë; X sekondë është e barabartë me minus dhjetë.
Mënyra e dytë
Nga vetia e logaritmeve, kemi dy logaritme dhjetore x është e barabartë me dy.
Rrënja e saj - x është e barabartë me dhjetë

Me metodën e dytë, rrënja x është e barabartë me minus dhjetë humbi. Dhe arsyeja është se ata aplikuan formulën e gabuar, duke ngushtuar shtrirjen e ekuacionit. Shprehja për logaritmin dhjetor të x në katror është përcaktuar për të gjithë x përveç x të barabartë me zero. Shprehja për logaritmin dhjetor të x është për x më e madhe se zero. Formula e saktë për logaritmin dhjetor x katror është e barabartë me modulin x dy logaritme dhjetore.
Mbani mend! Kur zgjidhni një ekuacion, përdorni me mençuri formulat e disponueshme.
Humbja e rrënjëve dhe rrënjëve të jashtme gjatë zgjidhjes së ekuacioneve
Institucioni arsimor komunal "Shkolla e mesme nr. 2 me studim të thelluar të lëndëve individuale" në qytetin e Vsevolozhsk. Puna kërkimore u përgatit nga një student i klasës 11 B: Vasilyev Vasily. Menaxheri i projektit: Egorova Lyudmila Alekseevna.
Ekuacioni Së pari, le të shohim mënyra të ndryshme për të zgjidhur këtë ekuacion sinx+cosx =- 1
Zgjidhja nr. 1 sinx+cosx =-1 i Y x 0 1 sin(x+)=- 1 sin(x+)=- x+ =- +2 x+ = +2 + x=- +2 x= +2 Përgjigje: + 2
Zgjidhja nr 2 sinx+cosx =- 1 i Përgjigje: +2 y x 0 1 2sin cos + - + + = 0 sin cos + = 0 cos (cos + sin)= 0 cos =0 cos + sin =1 = + m tg =-1 = + m =- + x=- +2 x= +2
Zgjidhja nr. 3 I y x 0 1 sinx+cosx =- 1 2 = x= x+ x sin2x=0 2x= x= Përgjigje:
sinx+cosx =-1 Zgjidhje nr 4 i y x 0 1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n Përgjigje: - + 2 n
Le të krahasojmë zgjidhjet Zgjidhjet e sakta Le të kuptojmë se në cilat raste mund të shfaqen rrënjë të jashtme dhe pse Nr. 2 Përgjigja: +2 Nr. 3 Përgjigjja: Nr.
Kontrollimi i zgjidhjes A është e nevojshme të kontrollohet? Kontrolloni rrënjët për çdo rast, për të qenë në anën e sigurt? Kjo sigurisht është e dobishme kur është e lehtë të zëvendësohet, por matematikanët janë njerëz racionalë dhe nuk bëjnë gjëra të panevojshme. Le të shohim raste të ndryshme dhe të kujtojmë kur verifikimi është vërtet i nevojshëm.
1. Formulat më të thjeshta të gatshme c osx =a x=a =a s inx =a t gx =a Në rastet kur rrënjët gjenden duke përdorur formulat më të thjeshta, të gatshme, kontrolli nuk ka nevojë të bëhet. Sidoqoftë, kur përdorni formula të tilla, duhet të mbani mend kushtet në të cilat ato mund të përdoren. Për shembull, formula = mund të përdoret nën kushtin a 0, -4ac 0 Dhe përgjigja x= arccos2+2 për ekuacionin cosx =2 konsiderohet një gabim bruto, pasi formula x= arccos a +2 mund të jetë vetëm përdoret për rrënjët e ekuacionit cosx =a, ku | a | 1
2. Transformimet Më shpesh, kur zgjidhni ekuacione, duhet të kryeni shumë transformime. Nëse një ekuacion zëvendësohet me një të ri që ka të gjitha rrënjët e atij të mëparshmi dhe ai transformohet në mënyrë që të mos ndodhë humbje ose përvetësim i rrënjëve, atëherë ekuacione të tilla quhen ekuivalente. 1. Gjatë transferimit të përbërësve të një ekuacioni nga një pjesë në tjetrën. 2. Kur shtoni të njëjtin numër në të dy anët. 3. Kur të dyja anët e një ekuacioni shumëzohen me të njëjtin numër jozero. 4 . Kur aplikoni identitete që janë të vërteta në grupin e të gjithë numrave realë. Sidoqoftë, verifikimi nuk kërkohet!
Megjithatë, jo çdo ekuacion mund të zgjidhet me transformime ekuivalente. Më shpesh është e nevojshme të aplikohen transformime të pabarabarta. Shpesh transformime të tilla bazohen në përdorimin e formulave që nuk janë të vlefshme për të gjitha vlerat reale. Në këtë rast, në veçanti, ndryshon fusha e përcaktimit të ekuacionit. Ky gabim gjendet në zgjidhjen #4. Le të shohim gabimin, por fillimisht le të shohim sërish zgjidhjen nr.4. sinx+cosx=-1 + =-1 2tg +1- =-1- 2tg =-2 =- + n x = - + 2 n Gabimi qëndron në formulën sin2x= Kjo formulë mund të përdoret, por duhet të kontrolloni më tej nëse rrënjët janë numra të formës + për të cilat tg nuk është përcaktuar. Tani është e qartë se zgjidhja është humbja e rrënjëve. Le ta shohim deri në fund.
Zgjidhje nr. 4 i y x 0 1 Le të kontrollojmë numrat = + n me zëvendësim: x= + 2 n sin(+ 2 n)+ cos (+ 2 n)=sin + cos =0+(-1)=- 1 Pra x= +2 n është rrënja e ekuacionit Përgjigje: +2 sinx+cosx =-1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n
Ne shikuam një nga mënyrat për të humbur rrënjët, ka shumë prej tyre në matematikë, kështu që ju duhet t'i zgjidhni me kujdes, duke mbajtur mend të gjitha rregullat. Ashtu siç mund të humbni rrënjët e një ekuacioni, mund të fitoni edhe ato shtesë gjatë zgjidhjes së tij. Le të shqyrtojmë zgjidhjen nr. 3 në të cilën është bërë një gabim i tillë.
Zgjidhja #3 I y x 0 1 2 2 dhe rrënjë shtesë! Rrënjët e jashtme mund të shfaqen kur të dyja anët e ekuacionit ishin në katror. Në këtë rast, është e nevojshme të kontrolloni. Për n=2k kemi sin k+cos k=-1; cos k=-1 për k=2m-1, atëherë n=2(2m+1)=4m+2, x= = +2 m, Përgjigje: +2 Për n=2k+1 kemi sin +cos =- 1 sin(+ k)+ cos (+ k)=- 1 cos k-sin k=- 1 cos k=-1 me k=2m+1 n=2(2m+1)+ 1=2m+3 x= ( 4m+3)= +2 m=- +2 sinx+cosx =- 1 = x= x+ x sin2x=0 2x= x=
Pra, ne shqyrtuam disa raste të mundshme, nga të cilat ka shumë. Mundohuni të mos e humbni kohën tuaj dhe të bëni gabime të trashë.
 Biografia e Manikhas Georgy Moiseevich
Biografia e Manikhas Georgy Moiseevich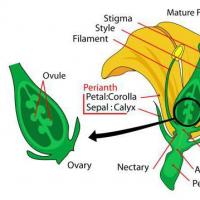 Botanika është një degë e shkencës së bimëve
Botanika është një degë e shkencës së bimëve Meditimi më efektiv në mëngjes, këshilla se si të meditoni në mëngjes
Meditimi më efektiv në mëngjes, këshilla se si të meditoni në mëngjes Si përdoret uji nga shtatë kishat?
Si përdoret uji nga shtatë kishat? Heqja e dëmit në kishë: fuqia e Zotit do të çlirojë nga një mallkim i fortë
Heqja e dëmit në kishë: fuqia e Zotit do të çlirojë nga një mallkim i fortë Si të hiqni negativitetin nga vetja në shtëpi: mënyra efektive
Si të hiqni negativitetin nga vetja në shtëpi: mënyra efektive