Kuras transformācijas neizraisa sakņu zudumu. Vienādojumu pārveidošana, ekvivalentie pārveidojumi. Saskaņā ar DL noteikumiem
Trigonometrisko vienādojumu tēma sākas ar skolas lekciju, kas ir strukturēta heiristiskas sarunas veidā. Lekcijā tiek apspriests teorētiskais materiāls un piemēri visu tipisko problēmu risināšanai pēc plāna:
- Vienkāršākie trigonometriskie vienādojumi.
- Trigonometrisko vienādojumu risināšanas pamatmetodes.
- Homogēni vienādojumi.
Turpmākajās nodarbībās sākas patstāvīga prasmju pilnveidošana, kuras pamatā ir skolotāja un skolēna kopīgās darbības principa pielietošana. Pirmkārt, tiek izvirzīti mērķi skolēniem, t.i. tiek noteikts, kurš vēlas zināt ne vairāk par to, ko prasa valsts standarts, un kurš ir gatavs darīt vairāk.
Galīgā diagnoze tiek veidota, ņemot vērā līmeņu diferenciāciju, kas ļauj studentiem apzināti noteikt minimālās zināšanas, kas nepieciešamas, lai saņemtu atzīmi “3”. Pamatojoties uz to, tiek atlasīti daudzlīmeņu materiāli, lai diagnosticētu studentu zināšanas. Šāds darbs ļauj veidot individuālu pieeju skolēniem, iekļaujot ikvienu apzinātās mācību aktivitātēs, attīstot pašorganizācijas un pašmācības prasmes un nodrošinot pāreju uz aktīvu, patstāvīgu domāšanu.
Seminārs tiek vadīts pēc trigonometrisko vienādojumu risināšanas pamatiemaņu praktizēšanas. Vairākas nodarbības pirms semināra studentiem tiek uzdoti jautājumi, kas tiks apspriesti semināra laikā.
Seminārs sastāv no trim daļām.
1. Ievaddaļa aptver visu teorētisko materiālu, ieskaitot ievadu problēmām, kas radīsies, risinot sarežģītus vienādojumus.
2. Otrajā daļā apskatīts formas vienādojumu risinājums:
- un cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- vienādojumi atrisināmi, samazinot pakāpi.
Šajos vienādojumos tiek izmantota universālā aizstāšana, pakāpes samazināšanas formulas un palīgargumentu metode.
3. Trešajā daļā aplūkotas sakņu zuduma un svešu sakņu iegūšanas problēmas. Parāda, kā atlasīt saknes.
Skolēni strādā grupās. Lai atrisinātu piemērus, tiek pieaicināti labi apmācīti puiši, kuri var parādīt un izskaidrot materiālu.
Seminārs paredzēts labi sagatavotam studentam, jo... tajā ir aplūkoti jautājumi, kas nedaudz pārsniedz programmas materiāla darbības jomu. Tas ietver sarežģītākas formas vienādojumus un jo īpaši pievēršas problēmām, kas rodas, risinot sarežģītus trigonometriskos vienādojumus.
Seminārs notika 10.-11.klašu skolēniem. Katram skolēnam bija iespēja paplašināt un padziļināt zināšanas par šo tēmu, salīdzināt savu zināšanu līmeni ne tikai ar prasībām skolas absolventam, bet arī ar prasībām, kas tiek izvirzītas V.U.Z.
SEMINĀRS
Temats:"Trigonometrisko vienādojumu risināšana"
Mērķi:
- Vispārināt zināšanas par visu veidu trigonometrisko vienādojumu risināšanu.
- Koncentrēties uz problēmām: sakņu zudums; svešas saknes; saknes atlase.
NODARBĪBU LAIKĀ.
I. Ievaddaļa
1. Trigonometrisko vienādojumu risināšanas pamatmetodes
- Faktorizācija.
- Jauna mainīgā lieluma ieviešana.
- Funkcionāli grafiskā metode.
2. Daži trigonometrisko vienādojumu veidi.
- Vienādojumi, kas reducējas uz kvadrātvienādojumiem attiecībā uz cos x = t, sin x = t.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Bsinx + C = 0.
Tie tiek atrisināti, ieviešot jaunu mainīgo.
- Pirmās un otrās pakāpes homogēnie vienādojumi
Pirmās pakāpes vienādojums: Asinx + Bcosx = 0 dalot ar cos x, iegūstam Atg x + B = 0
Otrās pakāpes vienādojums: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 dalot ar cos 2 x, iegūstam Atg 2 x + Btgx + C = 0
Tie tiek atrisināti, izmantojot faktorizāciju un ieviešot jaunu mainīgo.
Piemēro visas metodes.
- Pazemināt:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Atrisināts ar faktorizācijas metodi.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Formas vienādojums: A(sinx + cosx) + Bsin2x + C = 0.
Reducēts līdz kvadrātam attiecībā pret t = sinx + cosx; sin2x = t 2–1.
3. Formulas.
x + 2n; Nepieciešama pārbaude!
- Samazināšanās pakāpe: cos 2 x = (1 + cos2x): 2; grēks 2 x = (1 – cos 2x): 2
- Papildargumentu metode.
Aizstāt Acosx + Bsinx ar Csin (x + ), kur sin = a/C; cos=v/c;
– palīgarguments.
4. Noteikumi.
- Ja redzat kvadrātu, pazeminiet grādu.
- Ja redzi gabalu, sastādiet summu.
- Ja redzat summu, dariet darbu.
5. Sakņu zudums, papildu saknes.
- Sakņu zudums: dala ar g(x); bīstamas formulas (universāla aizstāšana). Ar šīm darbībām mēs sašaurinām definīcijas jomu.
- Papildu saknes: paceltas līdz vienmērīgai jaudai; reiziniet ar g(x) (atbrīvojieties no saucēja). Ar šīm darbībām mēs paplašinām definīcijas jomu.
II. Trigonometrisko vienādojumu piemēri
1. Formas vienādojumi Asinx + Bcosx = C
1) Universāla aizstāšana.O.D.Z. x – jebkurš.
3 grēks 2x + cos 2x + 1 = 0.
tgx = u. x/2 + n;
![]() u = – 1/3.
u = – 1/3.
iedegums x = –1/3, x = arctāns (–1/3) + k, k Z.
Pārbaude: 3sin( + 2n) + cos( + 2n) + 1= 3 sin + cos + 1 = 0 – 1 + 1 = 0.
x = /2 + n, n e Z. Ir vienādojuma sakne.
Atbilde: x = arctan(–1/3) + k, k Z. x = /2 + n, n Z.
2) Funkcionāli grafiskā metode. O.D.Z. x – jebkurš.
Sinx – cosx = 1
Sinx = cosx + 1.
Uzzīmēsim funkcijas: y = sinx, y = cosx + 1.

Atbilde: x = /2 + 2 n, Z; x = + 2k, k Z.
3) Papildargumenta ievads. O.D.Z.: x – jebkurš.
8cosx + 15 sinx = 17.
![]()
8/17 cosx + 15/17 sinx = 1, jo (8/17) 2 + (15/17) 2 = 1, tad pastāv tāds, ka grēks = 8/17,
cos = 15/17, kas nozīmē sin cosx + sinx cos = 1; = arcsin 8/17.
Atbilde: x = /2 + 2n – , x = /2 + 2n – arcsin 8/17, n Z.
2. Pasūtījuma samazināšana: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). grēks 2 3x + grēks 2 4x + grēks 2 6x + grēks 2 7x = 2. O.D.Z.: x – jebkurš.
1 - cos 6x + 1 - cos 8x + 1 - cos 12x + 1 - cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x (cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Atbilde: x = /20 + n/10, n Z. x = /6 + k/3, k Z, x = /2 + m, m Z.
| Plkst | k = 1 un m = 0 k = 4 un m = 1. |
sērijas ir vienādas. |
3. Samazināšana līdz viendabīgumam. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 3 sinx cosx + 6 cos 2 x = 5. ODZ: x – jebkurš.
5 sin 2 x + 3 sinx cosx + 6 cos 2 x – 5 sin 2 x - 5 cos 2 x = 0
3 sinxcosx + cos 2 x = 0 (1) nevar dalīt ar cos 2 x, jo mēs zaudējam saknes.
cos 2 x = 0 apmierina vienādojumu.
cosx (3 sinx + cosx) = 0
cosx = 0. 3 sinx + cosx = 0.
x = /2 + k, k Z. tgx = –1/3, x = –/6 + n, n Z.
Atbilde: x = /2 + k, k Z. , x = –/6 + n, n Z
4. Formas vienādojums: A(sinx + cosx) + B sin2x + C = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. O.D.Z.: x – jebkurš.
sinx + cosx = t, sin2x = t 2–1.
4 + 2t 2 – 2 – 5t = 0, | t | <
2
2 t 2 – 5 t + 2 = 0. t 1 = 2, t 2 = S.
sinx + cosx = S. cosx = sin(x + /2),
sinx + sin(x + /2) = 1/2,
2sin(x + /4) cos(–/4) = 1/2
sin(x + /4) = 1/22;
x +/4 = (–1) k arcsin(1/2 O 2) + k, k Z.
Atbilde: x = (–1) k arcsin(1/22) – /4 + k, k Z.
5. Faktorizācija.
1) cos 2 x – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2) (cosx + 2 sinx) = 0.
1) cosx = 2, bez saknēm.
2) cosx + 2 sinx = 0
2tgx + 1 = 0
Atbilde: x = arktāns(1/2) + n, n Z.
III. Problēmas, kas rodas, risinot trigonometriskos vienādojumus
1. Sakņu zudums: dala ar g(x); Mēs izmantojam bīstamas formulas.
1) Atrodiet kļūdu.
1 – cosx = sinx *sinx/2,
1 – cosx = 2sin 2 x/2 formula.
2 sin 2 x/2 = 2 sinx/2* сosx/2* sinx/2 dalīt ar 2 sin 2 x/2,
1 = cosx/2
x/2 = 2n, x = 4n, n" Z.
Zaudētās saknes sinx/2 = 0, x = 2k, k Z.
Pareizs risinājums: 2sin 2 x/2(1 – cosx/2) = 0.
| grēks 2 x/2 = 0 x = 2k, k Z. |
1 – cosx /2 = 0 x = 4p n, n Z. |
2. Svešas saknes: atbrīvojamies no saucēja; paaugstināt līdz vienmērīgai jaudai.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 3) = 0. O.D.Z.: sin2x 3/2.
2сos3х sinx – сos3x + 2sinx – 1 = 0
(cos3x + 1) (2sinx – 1) = 0
| 1). сos3x + 1 = 0 x = /3 + 2n/3, n Z. |
2). 2sinx – 1 = 0 x = (–1) k /6 + k, k Z. |

| I. x = /3 + 2n/3 1. n = 0 grēks 2/3 = 3/2 neapmierina. O.D.Z. 2. n = 1 3. n = 2 |
II. x = (–1) k /6 + k, k Z 1.k = 0 grēks 2/6 = 3/2 neapmierina O.D.Z. 2. k = 1 grēks 2*5/6 = –3/2 apmierināt O.D.Z. |
Atbilde: x = + 2k, x = 5/3 + 2k, x = 5/6 + 2k, k Z. t = 5 sin3x = 0
Vienādojumu risināšanas pamatmetodes
Kāds ir vienādojuma risinājums?
Identiska transformācija. Pamata
identitātes transformāciju veidi.
Ārzemju sakne. Sakņu zudums.
Vienādojuma atrisināšana ir process, kas galvenokārt sastāv no dotā vienādojuma aizstāšanas ar citu vienādojumu, kas tam ir līdzvērtīgs . Šo nomaiņu saucidentiska transformācija . Galvenās identitātes transformācijas ir šādas:
1.
Vienas izteiksmes aizstāšana ar citu, kas ir identiski vienāda ar to. Piemēram, vienādojums (3 x+ 2 ) 2 = 15 x+ 10 var aizstāt ar šādu ekvivalentu:9 x 2 + 12 x+ 4 = 15 x+ 10 .
2.
Vienādojuma nosacījumu pārnešana no vienas puses uz otru ar apgrieztām zīmēm. Tātad, iepriekšējā vienādojumā mēs varam pārnest visus tā nosacījumus no labās puses uz kreiso pusi ar “-” zīmi: 9 x 2 + 12 x+ 4 – 15 x – 10 = 0, pēc kura mēs iegūstam:9 x 2 – 3 x – 6 = 0 .
3.
Vienādojuma abu pušu reizināšana vai dalīšana ar vienu un to pašu izteiksmi (skaitli), kas nav nulle. Tas ir ļoti svarīgi, jojaunais vienādojums var nebūt līdzvērtīgs iepriekšējam, ja izteiksme, ar kuru mēs reizinām vai dalām, var būt vienāda ar nulli.
PIEMĒRS Vienādojumsx – 1 = 0 ir viena saknex = 1.
Reizinot abas puses arx – 3 , mēs iegūstam vienādojumu
( x – 1)( x – 3) = 0, kam ir divas saknes:x = 1 unx = 3.
Pēdējā vērtība nav dotā vienādojuma sakne
x – 1 = 0. Tas ir tā sauktaissveša sakne .
Un otrādi, sadalīšana var novest piesakņu zudums . Tātad
mūsu gadījumā, ja (x – 1 )( x – 3 ) = 0 ir oriģināls
vienādojums, tad saknex = 3 tiks zaudēti divīzijā
abas vienādojuma puses ieslēgtasx – 3 .
Pēdējā vienādojumā (2. punkts) visus tā nosacījumus varam dalīt ar 3 (nevis nulli!) un visbeidzot iegūt:
3 x 2 – x – 2 = 0 .
Šis vienādojums ir līdzvērtīgs sākotnējam:
(3 x+ 2) 2 = 15 x+ 10 .
4.
Varpaaugstiniet abas vienādojuma puses līdz nepāra pakāpei vaiizņemiet nepāra sakni no abām vienādojuma pusēm . Jāatceras, ka:
a) būvniecība iekšāvienmērīgs grāds var izraisītsvešu sakņu iegūšanai ;
b)nepareizi ieguvepat sakne var novest piesakņu zudums .
PIEMĒRI. 7. vienādojumsx = 35 ir viena saknex = 5 .
Izliekot kvadrātā abas šī vienādojuma puses, mēs iegūstam
vienādojums:
49 x 2 = 1225 .
kam ir divas saknes:x = 5 Unx = – 5. Pēdējā vērtība
ir sveša sakne.
Nepareizi ņemot kvadrātsakni no abiem
49. vienādojuma daļasx 2 = 1225 rezultāti 7x = 35,
un mēs zaudējam savas saknesx = – 5.
Pareizi ņemot kvadrātsakni rezultātus
vienādojums: | 7x | = 35, A tātad divos gadījumos:
1) 7 x = 35, Tadx = 5 ; 2) – 7 x = 35, Tadx = – 5 .
Tāpēc, kadpareizi kvadrāta iegūšana
saknes mēs nezaudējam vienādojuma saknes.
Ko nozīmēPa labi izvilkt sakni? Šeit mēs tiekamies
ar ļoti svarīgu koncepcijuaritmētiskā sakne
(cm. ).
Var izraisīt tā saukto svešo sakņu parādīšanos. Šajā rakstā mēs vispirms detalizēti analizēsim, kas ir svešas saknes. Otrkārt, parunāsim par to rašanās iemesliem. Un, treškārt, izmantojot piemērus, mēs apsvērsim galvenās svešo sakņu filtrēšanas metodes, tas ir, pārbaudot saknes, vai starp tām nav svešu sakņu, lai tās izslēgtu no atbildes.
Vienādojuma svešās saknes, definīcija, piemēri
Skolas algebras mācību grāmatas nesniedz svešas saknes definīciju. Tur ideja par svešu sakni tiek veidota, aprakstot šādu situāciju: ar dažu vienādojuma pārveidojumu palīdzību tiek veikta pāreja no sākotnējā vienādojuma uz korolāro vienādojumu, tiek atrastas iegūtā korolārā vienādojuma saknes. , un atrastās saknes tiek pārbaudītas, aizstājot to sākotnējā vienādojumā, kas parāda, ka dažas no atrastajām saknēm nav sākotnējā vienādojuma saknes, šīs saknes sākotnējā vienādojumā sauc par svešām saknēm.
Sākot no šīs bāzes, jūs varat pieņemt šādu svešas saknes definīciju:
Definīcija
Svešas saknes- tās ir pārveidojumu rezultātā iegūtā korolārā vienādojuma saknes, kas nav sākotnējā vienādojuma saknes.
Sniegsim piemēru. Apskatīsim vienādojumu un šī vienādojuma sekas x·(x−1)=0, kas iegūts, aizstājot izteiksmi ar identiski vienādu izteiksmi x·(x−1) . Sākotnējam vienādojumam ir viena sakne 1. Transformācijas rezultātā iegūtajam vienādojumam ir divas saknes 0 un 1. Tas nozīmē, ka 0 ir sākotnējā vienādojuma sveša sakne.
Iespējamās svešzemju sakņu parādīšanās iemesli
Ja secīgā vienādojuma iegūšanai neizmanto nekādus “eksotiskus” pārveidojumus, bet izmanto tikai vienādojumu pamata transformācijas, tad svešas saknes var rasties tikai divu iemeslu dēļ:
- sakarā ar ODZ paplašināšanos un
- sakarā ar vienādojuma abu pušu paaugstināšanu līdz vienādam jaudai.
Šeit ir vērts atgādināt, ka ODZ paplašināšanās vienādojuma pārveidošanas rezultātā galvenokārt notiek
- Samazinot frakcijas;
- Aizstājot produktu ar vienu vai vairākiem nulles koeficientiem ar nulli;
- Aizstājot daļu ar nulles skaitītāju ar nulli;
- Lietojot dažas pakāpju, sakņu, logaritmu īpašības;
- Lietojot dažas trigonometriskās formulas;
- Ja abas vienādojuma puses tiek reizinātas ar vienu un to pašu izteiksmi, tas pazūd ar šī vienādojuma ODZ;
- Atbrīvojoties no logaritma zīmēm risinājuma procesā.
Piemērs no raksta iepriekšējās rindkopas ilustrē svešas saknes parādīšanos ODZ paplašināšanās dēļ, kas rodas, pārejot no vienādojuma uz konsekvento vienādojumu x·(x−1)=0. Sākotnējā vienādojuma ODZ ir visu reālo skaitļu kopa, izņemot nulli, iegūtā vienādojuma ODZ ir kopa R, tas ir, ODZ tiek paplašināts ar skaitli nulle. Šis skaitlis galu galā izrādās sveša sakne.
Mēs arī sniegsim piemēru par svešas saknes parādīšanos, kas rodas, paaugstinot abas vienādojuma puses līdz vienādam jaudai. Iracionālajam vienādojumam ir viena sakne 4, un šī vienādojuma sekas, kas iegūtas no tā, izliekot kvadrātā abas vienādojuma puses, tas ir, vienādojums ![]() , ir divas saknes 1 un 4. No tā ir skaidrs, ka vienādojuma abu pušu sadalīšana kvadrātā izraisīja svešas saknes parādīšanos sākotnējam vienādojumam.
, ir divas saknes 1 un 4. No tā ir skaidrs, ka vienādojuma abu pušu sadalīšana kvadrātā izraisīja svešas saknes parādīšanos sākotnējam vienādojumam.
Ņemiet vērā, ka ODZ paplašināšana un vienādojuma abu pušu paaugstināšana līdz vienādam jaudai ne vienmēr noved pie svešu sakņu parādīšanās. Piemēram, pārejot no vienādojuma uz izrietošo vienādojumu x=2, ODZ izplešas no visu nenegatīvo skaitļu kopas uz visu reālo skaitļu kopu, bet neparādās nekādas svešas saknes. 2 ir vienīgā sakne gan pirmajam, gan otrajam vienādojumam. Tāpat, pārejot no vienādojuma uz secīgu vienādojumu, neparādās svešas saknes. Pirmā un otrā vienādojuma vienīgā sakne ir x=16. Tāpēc mēs nerunājam par svešas izcelsmes sakņu parādīšanās iemesliem, bet gan par svešas izcelsmes sakņu parādīšanās iemesliem.
Kas ir svešu sakņu izsijāšana?
Jēdzienu “svešzemju sakņu izsijāšana” var saukt tikai par pastāvīgu, tas nav atrodams visās algebras mācību grāmatās, taču tas ir intuitīvs, tāpēc to parasti lieto. Kas tiek domāts ar svešu sakņu izsijāšanu, kļūst skaidrs no šādas frāzes: “... pārbaude ir obligāts solis vienādojuma risināšanā, kas palīdzēs atklāt svešas saknes, ja tādas ir, un tās izmest (parasti saka: “izravēt ”).”
Tādējādi
Definīcija
Svešo sakņu izsijāšana- tā ir svešu sakņu noteikšana un izmešana.
Tagad varat pāriet uz svešu sakņu izsijāšanas metodēm.
Metodes svešzemju sakņu izsijāšanai
Aizstāšanas pārbaude
Galvenais veids, kā filtrēt svešas saknes, ir aizstāšanas tests. Tas ļauj atsijāt svešas saknes, kas varētu rasties gan ODZ paplašināšanās dēļ, gan abu vienādojuma pušu paaugstināšanas dēļ līdz vienādam jaudai.
Aizstāšanas tests ir šāds: atrastās sekas vienādojuma saknes pēc kārtas tiek aizstātas sākotnējā vienādojumā vai jebkurā tam līdzvērtīgā vienādojumā, tās, kas dod pareizo skaitlisko vienādojumu, ir sākotnējā vienādojuma saknes, bet tās, kas dod nepareiza skaitliskā vienādība vai izteiksme ir sākotnējā vienādojuma saknes, kas ir svešas sākotnējā vienādojuma saknes.
Parādīsim ar piemēru, kā izfiltrēt svešas saknes, aizstājot to sākotnējā vienādojumā.
Dažos gadījumos ir lietderīgāk filtrēt svešas saknes, izmantojot citas metodes. Tas galvenokārt attiecas uz gadījumiem, kad pārbaude ar aizstāšanu ir saistīta ar būtiskām skaitļošanas grūtībām vai kad noteikta veida vienādojumu risināšanas standarta metode prasa citu pārbaudi (piemēram, svešu sakņu izsijāšana, risinot daļējos racionālos vienādojumus, tiek veikta saskaņā ar nosacījums, ka daļdaļas saucējs nav vienāds ar nulli ). Apskatīsim alternatīvus veidus, kā atsijāt svešas saknes.
Saskaņā ar DL
Atšķirībā no testēšanas ar aizstāšanu, svešu sakņu filtrēšana, izmantojot ODZ, ne vienmēr ir piemērota. Fakts ir tāds, ka šī metode ļauj filtrēt tikai svešas saknes, kas rodas ODZ paplašināšanās dēļ, un tā negarantē svešu sakņu izsijāšanu, kas varētu rasties citu iemeslu dēļ, piemēram, abu pušu pacelšanas dēļ. vienādojuma ar tādu pašu vienmērīgu jaudu . Turklāt ne vienmēr ir viegli atrast atrisināmā vienādojuma OD. Tomēr svešu sakņu izsijāšanas metodi, izmantojot ODZ, ir vērts paturēt ekspluatācijā, jo tās izmantošana bieži prasa mazāk skaitļošanas darba nekā citu metožu izmantošana.
Ārējo sakņu izravēšana saskaņā ar ODZ tiek veikta šādi: tiek pārbaudītas visas atrastās sekas vienādojuma saknes, lai noskaidrotu, vai tās ietilpst sākotnējā vienādojuma vai jebkura tam līdzvērtīga vienādojuma mainīgā pieļaujamo vērtību diapazonā, tie, kas pieder pie ODZ, ir sākotnējā vienādojuma saknes, un tie, kas pieder pie ODZ, ir sākotnējā vienādojuma saknes, un tie, kas nepieder ODZ, ir sākotnējā vienādojuma svešas saknes.
Sniegtās informācijas analīze ļauj secināt, ka ir ieteicams izsijāt svešas saknes, izmantojot ODZ, ja vienlaikus:
- ir viegli atrast oriģinālā vienādojuma ODZ,
- svešas saknes varēja rasties tikai ODZ paplašināšanās dēļ,
- Aizvietošanas testēšana ir saistīta ar ievērojamām skaitļošanas grūtībām.
Mēs parādīsim, kā praksē tiek veikta svešu sakņu ravēšana.
Saskaņā ar DL noteikumiem
Kā jau teicām iepriekšējā punktā, ja svešas saknes varētu rasties tikai ODZ paplašināšanās dēļ, tad tās var novērst, izmantojot ODZ sākotnējam vienādojumam. Bet ne vienmēr ir viegli atrast ODZ skaitliskās kopas formā. Šādos gadījumos ir iespējams izsijāt svešas saknes nevis saskaņā ar ODZ, bet gan atbilstoši nosacījumiem, kas nosaka ODZ. Paskaidrosim, kā ODZ apstākļos tiek veikta svešu sakņu ravēšana.
Atrastās saknes savukārt tiek aizstātas ar nosacījumiem, kas nosaka ODZ sākotnējam vienādojumam vai jebkuram tam līdzvērtīgam vienādojumam. Tie, kas atbilst visiem nosacījumiem, ir vienādojuma saknes. Un tie no tiem, kas neatbilst vismaz vienam nosacījumam vai nedod izteiksmi, kam nav jēgas, ir sākotnējā vienādojuma svešas saknes.
Sniegsim piemēru svešu sakņu izsijāšanai atbilstoši ODZ nosacījumiem.
Svešo sakņu atsijāšana, kas rodas, paaugstinot abas vienādojuma puses līdz vienmērīgai jaudai
Ir skaidrs, ka svešas saknes, kas rodas, paaugstinot abas vienādojuma puses līdz vienādam jaudai, var tikt veiktas, aizstājot to sākotnējā vienādojumā vai jebkurā tam līdzvērtīgā vienādojumā. Taču šāda pārbaude var būt saistīta ar ievērojamām skaitļošanas grūtībām. Šajā gadījumā ir vērts zināt alternatīvu svešas izcelsmes sakņu izsijāšanas metodi, par kuru mēs tagad runāsim.
Izsijāt svešas saknes, kas var rasties, paaugstinot formas iracionālo vienādojumu abas puses līdz vienādam jaudai ![]() , kur n ir kāds pāra skaitlis, var izpildīt saskaņā ar nosacījumu g(x)≥0. Tas izriet no pāra pakāpes saknes definīcijas: pāra pakāpes sakne n ir nenegatīvs skaitlis, kura n-tā pakāpe ir vienāda ar radikālo skaitli, no kurienes
, kur n ir kāds pāra skaitlis, var izpildīt saskaņā ar nosacījumu g(x)≥0. Tas izriet no pāra pakāpes saknes definīcijas: pāra pakāpes sakne n ir nenegatīvs skaitlis, kura n-tā pakāpe ir vienāda ar radikālo skaitli, no kurienes  . Tādējādi paustā pieeja ir sava veida simbioze metodei, kā vienādojuma abas puses paaugstina vienādībā, un iracionālo vienādojumu atrisināšanas metodei, nosakot sakni. Tas ir, vienādojums
. Tādējādi paustā pieeja ir sava veida simbioze metodei, kā vienādojuma abas puses paaugstina vienādībā, un iracionālo vienādojumu atrisināšanas metodei, nosakot sakni. Tas ir, vienādojums ![]() , kur n ir pāra skaitlis, tiek atrisināts, paaugstinot abas vienādojuma puses līdz vienādai pāra pakāpei, un svešu sakņu likvidēšana tiek veikta saskaņā ar nosacījumu g(x)≥0, kas ņemts no iracionālu vienādojumu atrisināšanas metodes ar saknes noteikšana.
, kur n ir pāra skaitlis, tiek atrisināts, paaugstinot abas vienādojuma puses līdz vienādai pāra pakāpei, un svešu sakņu likvidēšana tiek veikta saskaņā ar nosacījumu g(x)≥0, kas ņemts no iracionālu vienādojumu atrisināšanas metodes ar saknes noteikšana.
Pēdējā nodarbībā vienādojumu risināšanai izmantojām trīs soļus.
Pirmais posms ir tehnisks. Izmantojot transformāciju ķēdi no sākotnējā vienādojuma, mēs nonākam pie diezgan vienkārša, kuru atrisinām un atrodam saknes.
Otrais posms ir risinājuma analīze. Mēs analizējam veiktās transformācijas un noskaidrojam, vai tās ir līdzvērtīgas.
Trešais posms ir pārbaude. Visu atrasto sakņu pārbaude, aizvietojot tās sākotnējā vienādojumā, ir obligāta, veicot transformācijas, kas var novest pie secinājuma vienādojuma
Vai, risinot vienādojumu, vienmēr ir jānošķir trīs posmi?
Protams, nē. Kā, piemēram, risinot šo vienādojumu. Ikdienā tos parasti neatšķir. Bet visi šie posmi ir “jāpatur prātā” un jāveic vienā vai otrā veidā. Ir obligāti jāanalizē transformāciju līdzvērtība. Un, ja analīze parāda, ka ir jāveic pārbaude, tad tā ir obligāta. Pretējā gadījumā vienādojumu nevar uzskatīt par pareizi atrisinātu.
Vai vienmēr ir iespējams pārbaudīt vienādojuma saknes tikai ar aizstāšanu?
Ja, risinot vienādojumu, tika izmantotas līdzvērtīgas transformācijas, tad pārbaude nav nepieciešama. Pārbaudot vienādojuma saknes, ļoti bieži tiek izmantots ODZ (pieļaujamo vērtību diapazons). Ja to ir grūti pārbaudīt, izmantojot ODZ, tad to veic, aizstājot to sākotnējā vienādojumā.
1. vingrinājums
Atrisiniet vienādojumu kvadrātsakne no divi x plus trīs ir vienāds ar vienu plus x.
Risinājums
Vienādojuma ODZ nosaka divu nevienādību sistēma: divi x plus trīs ir lielāks vai vienāds ar nulli un viens plus x ir lielāks vai vienāds ar nulli. Risinājums ir x lielāks vai vienāds ar mīnus viens.
Izlīdzināsim abas vienādojuma puses kvadrātā, pārvietosim vārdus no vienas vienādojuma puses uz otru, pievienosim līdzīgus vārdus un iegūsim kvadrātvienādojumu x kvadrātā ir vienāds ar diviem. Tās saknes ir
x pirmais, otrais ir vienāds ar plus vai mīnus kvadrātsakni no diviem.
Pārbaude
Vērtība x vispirms ir vienāda ar kvadrātsakni no diviem, kas ir vienādojuma sakne, jo tas ir iekļauts ODZ.
Vērtība x sekundes ir vienāda ar mīnus kvadrātsakni no diviem nav vienādojuma sakne, jo tas nav iekļauts DZ.
Pārbaudīsim, ka sakne x ir vienāda ar kvadrātsakni no diviem, aizstājot to sākotnējā vienādībā, mēs iegūstam
vienādība ir patiesa, kas nozīmē, ka x ir vienāds ar kvadrātsakni no diviem, ir vienādojuma sakne.
Atbilde: kvadrātsakne no diviem.
2. uzdevums
Atrisiniet vienādojumu kvadrātsakne no x mīnus astoņi ir vienāds ar pieci mīnus x.
Risinājums
Iracionāla vienādojuma ODZ nosaka divu nevienādību sistēma: x mīnus astoņi ir lielāka vai vienāda ar nulli un pieci mīnus x ir lielāka vai vienāda ar nulli. Atrisinot to, mēs atklājam, ka šai sistēmai nav risinājumu. Vienādojuma sakne nevar būt neviena no mainīgā x vērtībām.
Atbilde: nav sakņu.
3. uzdevums
Atrisiniet vienādojumu kvadrātsakne no x x kuba plus četri x mīnus viens mīnus astoņas kvadrātsaknes no x līdz ceturtajai pakāpei mīnus x ir vienāda ar kvadrātsakni no x kuba mīnus viens plus divas kvadrātsaknes no x.
Risinājums
ODZ atrašana šajā vienādojumā ir diezgan sarežģīta.
Veiksim transformāciju: kvadrātā abas šī vienādojuma puses,
Pārvietosim visus vārdus uz vienādojuma kreiso pusi un izveidosim līdzīgus vārdus, zem viena uzrakstīsim divas saknes, iegūstam līdzīgus radikāļus, izveidosim līdzīgus, dalīsim ar koeficientu mīnus 12 un faktorējam radikāļu izteiksmi, iegūstam vienādojumu divu faktoru reizinājuma forma, kas vienāda ar nulli. Atrisinot to, mēs atrodam saknes:
x pirmais ir vienāds ar vienu, x otrais ir vienāds ar nulli.
Tā kā mēs paaugstinājām abas vienādojuma puses līdz vienmērīgai pakāpei, sakņu pārbaude ir obligāta.
Pārbaude
Ja x ir vienāds ar vienu, tad
mēs iegūstam pareizo vienādību, kas nozīmē, ka x ir vienāds ar vienu, ir vienādojuma sakne.

Ja x ir nulle, tad kvadrātsakne no mīnus viens nav definēta.
Tas nozīmē, ka x vienāds ar nulli ir sveša sakne.
Atbilde: viens.
4. uzdevums
Atrisiniet vienādojuma logaritmu izteiksmei x kvadrātā plus pieci x plus divi bāze divi ir vienāds ar trīs.
Risinājums
Atradīsim ODZ vienādojumu. Lai to izdarītu, mēs atrisinām nevienādību x kvadrātā plus pieci x plus divi virs nulles.
Nevienādību risinām, izmantojot intervāla metodi. Lai to izdarītu, mēs faktorizējam tā kreiso pusi, iepriekš atrisinot kvadrātvienādojumu, un, ņemot vērā nevienlīdzības zīmi, mēs nosakām ODZ. ODZ ir vienāds ar atvērto staru savienojumu no mīnus bezgalības līdz mīnus daļai pieci plus kvadrātsakne no septiņpadsmit, dalīta ar divi, un no mīnus daļdaļas pieci mīnus kvadrātsakne no septiņpadsmit, dalīta ar divi, līdz plus bezgalība.
Tagad sāksim atrast vienādojuma saknes. Ņemot vērā, ka trīs ir vienāds ar logaritmu no astoņiem pret bāzi divi, mēs rakstām vienādojumu šādi: izteiksmes x kvadrāts plus pieci x plus divi pret bāzi divi ir vienāds ar logaritmu astoņi pret bāzi divi. Potencēsim vienādojumu, iegūsim un atrisināsim kvadrātvienādojumu.
Diskriminants ir četrdesmit deviņi.
Aprēķiniet saknes:
x pirmais ir vienāds ar mīnus seši; x sekunde ir vienāda ar vienu.
Pārbaude
Mīnus seši pieder ODZ, viens pieder ODZ, kas nozīmē, ka abi skaitļi ir vienādojuma saknes.
Atbilde: mīnus seši; viens.
Pēdējā nodarbībā apskatījām jautājumu par svešu sakņu parādīšanos. Mēs varam tos atklāt, veicot verifikāciju. Vai, risinot vienādojumu, ir iespējams zaudēt saknes un kā to novērst?
Veicot tādas darbības ar vienādojumu, piemēram, pirmkārt, sadalot abas vienādojuma puses ar vienu un to pašu izteiksmi ax no x (izņemot gadījumus, kad ir droši zināms, ka ax no x nav vienāds ar nulli nevienam x no x vienādojuma definīcijas joma) ;
otrkārt, vienādojuma OD sašaurināšanās risināšanas procesa laikā var novest pie vienādojuma sakņu zaudēšanas.
Atcerieties!

Vienādojums, kas uzrakstīts kā
ef no x reizināts ar pelniem no x ir vienāds ar zhe no x reizināts ar pelniem no x tiek atrisināts šādi:
nepieciešams veikt koeficientu, izliekot kopējo koeficientu iekavās;
tad pielīdziniet katru koeficientu nullei, tādējādi iegūstot divus vienādojumus.
Mēs aprēķinām to saknes.
1. vingrinājums
Atrisiniet vienādojumu x kubs ir vienāds ar x.
Pirmais veids
Sadaliet abas šī vienādojuma puses ar x, iegūstam x kvadrāts ir vienāds ar vienu, kam saknes x vispirms ir vienāds ar vienu,
x sekunde ir vienāda ar mīnus viens.
Otrais veids
X kubs ir vienāds ar X. Pārvietosim x uz vienādojuma kreiso pusi, izņemam x no iekavām un iegūstam: x reizināts ar x kvadrātā mīnus viens ir vienāds ar nulli.
Aprēķināsim tā saknes:
X pirmais ir vienāds ar nulli, x second ir vienāds ar vienu, x trešais ir vienāds ar mīnus viens.
Vienādojumam ir trīs saknes.
Atrisinot pirmo metodi, mēs zaudējām vienu sakni - x ir vienāds ar nulli.
Atbilde: mīnus viens; nulle; viens.
Atcerieties! Samazinot abas vienādojuma puses ar koeficientu, kas satur nezināmo, var tikt zaudētas saknes.
2. uzdevums
Atrisiniet vienādojumu: x decimāllogaritms kvadrātā ir vienāds ar divi.
Risinājums
Pirmais veids
Pēc logaritma definīcijas mēs iegūstam kvadrātvienādojumu x kvadrāts ir vienāds ar simtu.
Tās saknes: x vispirms ir vienāds ar desmit; X sekunde ir vienāda ar mīnus desmit.
Otrais veids
Pēc logaritmu īpašībām mums ir divi decimāllogaritmi x ir vienāds ar diviem.
Tās sakne - x ir vienāda ar desmit

Ar otro metodi sakne x ir vienāda ar mīnus desmit tika zaudēta. Un iemesls ir tas, ka viņi izmantoja nepareizu formulu, sašaurinot vienādojuma darbības jomu. Decimāllogaritma x kvadrātā izteiksme ir definēta visiem x, izņemot x, kas ir vienāda ar nulli. X decimāllogaritma izteiksme ir x lielāka par nulli. Pareizā decimāllogaritma x kvadrāta formula ir vienāda ar divu decimālo logaritmu moduli x.
Atcerieties! Atrisinot vienādojumu, saprātīgi izmantojiet pieejamās formulas.
Sakņu un svešu sakņu zudums, risinot vienādojumus
Pašvaldības izglītības iestāde "2. vidusskola ar padziļinātu atsevišķu priekšmetu apguvi" Vsevoložskas pilsētā. Pētniecisko darbu sagatavoja 11. B klases skolēns: Vasiļjevs Vasilijs. Projekta vadītāja: Egorova Ludmila Alekseevna.
Vienādojums Vispirms apskatīsim dažādus veidus, kā atrisināt šo vienādojumu sinx+cosx =- 1
Risinājums Nr.1 sinx+cosx =-1 i Y x 0 1 sin(x+)=- 1 sin(x+)=- x+ =- +2 x+ = +2 + x=- +2 x= +2 Atbilde: + 2
Risinājums Nr. 2 sinx+cosx =- 1. Atbilde: +2 y x 0 1 2sin cos + - + + = 0 sin cos + = 0 cos (cos + sin)= 0 cos =0 cos + sin =1 = + m tg =-1 = + m =- + x=- +2 x= +2
Risinājums Nr. 3 I y x 0 1 sinx+cosx =- 1 2 = x= x+ x sin2x=0 2x= x= Atbilde:
sinx+cosx =-1 Risinājums Nr. 4 i y x 0 1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n Atbilde: - + 2 n
Salīdzināsim risinājumus Pareizie risinājumi Noskaidrosim, kādos gadījumos var parādīties svešas saknes un kāpēc Nr.2 Atbilde: +2 Nr.3 Atbilde: Nr.4 Atbilde: + 2n Nr.1 Atbilde: +2
Risinājuma pārbaude Vai ir nepieciešams pārbaudīt? Vai man vajadzētu pārbaudīt saknes katram gadījumam, lai būtu drošībā? Tas, protams, ir noderīgi, ja to ir viegli aizstāt, bet matemātiķi ir racionāli cilvēki un nedara nevajadzīgas lietas. Apskatīsim dažādus gadījumus un atcerēsimies, kad verifikācija patiešām ir nepieciešama.
1. Vienkāršākās gatavās formulas c osx =a x=a =a s inx =a t gx =a Gadījumos, kad saknes atrod, izmantojot visvienkāršākās, gatavās formulas, pārbaude nav jāveic. Tomēr, izmantojot šādas formulas, jāatceras, kādos apstākļos tās var izmantot. Piemēram, formulu = var izmantot ar nosacījumu a 0, -4ac 0 Un atbilde x= arccos2+2 vienādojumam cosx =2 tiek uzskatīta par rupju kļūdu, jo formula x= arccos a +2 var būt tikai izmanto vienādojuma cosx =a saknēm, kur | a | 1
2. Transformācijas Biežāk, risinot vienādojumus, ir jāveic daudz pārveidojumu. Ja vienādojumu aizstāj ar jaunu, kuram ir visas iepriekšējā saknes, un tas tiek pārveidots tā, ka nerodas sakņu zudumi vai iegūšana, tad šādus vienādojumus sauc par ekvivalentiem. 1. Pārnesot vienādojuma sastāvdaļas no vienas daļas uz otru. 2. Pievienojot vienu un to pašu numuru abām pusēm. 3. Kad abas vienādojuma puses tiek reizinātas ar vienu un to pašu skaitli, kas nav nulle. 4 . Lietojot identitātes, kas ir derīgas visu reālo skaitļu kopai. Tomēr pārbaude nav nepieciešama!
Tomēr ne katru vienādojumu var atrisināt ar līdzvērtīgām transformācijām. Biežāk ir jāpiemēro nevienlīdzīgas pārvērtības. Bieži vien šādas transformācijas ir balstītas uz tādu formulu izmantošanu, kuras nav derīgas visām reālajām vērtībām. Šajā gadījumā jo īpaši mainās vienādojuma definīcijas joma. Šī kļūda ir atrodama 4. risinājumā. Apskatīsim kļūdu, bet vispirms vēlreiz apskatīsim risinājumu Nr.4. sinx+cosx=-1 + =-1 2tg +1- =-1- 2tg =-2 =- + n x = - + 2 n Kļūda slēpjas formulā sin2x= Šo formulu var izmantot, bet jums vajadzētu papildus pārbaudīt vai saknes ir skaitļi formā +, kuriem tg nav definēts. Tagad ir skaidrs, ka risinājums ir sakņu zaudēšana. Paskatīsimies līdz galam.
Risinājums Nr.4 i y x 0 1 Pārbaudīsim skaitļus = + n ar aizstāšanu: x= + 2 n sin(+ 2 n)+ cos (+ 2 n)=sin + cos =0+(-1)=- 1 Tātad x= +2 n ir vienādojuma sakne Atbilde: +2 sinx+cosx =-1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n
Mēs apskatījām vienu no veidiem, kā zaudēt saknes, matemātikā to ir ļoti daudz, tāpēc jums tas ir rūpīgi jāatrisina, atceroties visus noteikumus. Tāpat kā vienādojuma saknes var pazaudēt, tā risināšanas gaitā var iegūt arī papildu saknes. Apskatīsim risinājumu Nr.3, kurā tika pieļauta šāda kļūda.
3. risinājums I y x 0 1 2 2 un papildu saknes! Svešas saknes varētu parādīties, kad abas vienādojuma puses ir kvadrātā. Šajā gadījumā ir nepieciešams pārbaudīt. Ja n=2k mums ir sin k+cos k=-1; cos k=-1 pie k=2m-1 , Tad n=2(2m+1)=4m+2 , x= = +2 m , Atbilde: +2 Par n=2k+1 mums ir sin +cos =- 1 sin(+ k)+ cos (+ k)=- 1 cos k-sin k=- 1 cos k=-1 ar k=2m+1 n=2(2m+1)+ 1=2m+3 x= (4m+3)= +2 m=- +2 sinx+cosx =- 1 = x= x+ x sin2x=0 2x= x=
Tātad, mēs apskatījām dažus iespējamos gadījumus, kuru ir ļoti daudz. Centieties netērēt savu laiku un nepieļaut stulbas kļūdas.
 Manikhas Georgija Moisejeviča biogrāfija
Manikhas Georgija Moisejeviča biogrāfija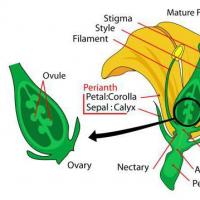 Botānika ir augu zinātnes nozare
Botānika ir augu zinātnes nozare Visefektīvākā rīta meditācija, padomi, kā meditēt no rīta
Visefektīvākā rīta meditācija, padomi, kā meditēt no rīta Kā tiek izmantots ūdens no septiņām baznīcām?
Kā tiek izmantots ūdens no septiņām baznīcām? Baznīcas bojājumu novēršana: Tā Kunga spēks atbrīvos jūs no spēcīga lāsta
Baznīcas bojājumu novēršana: Tā Kunga spēks atbrīvos jūs no spēcīga lāsta Kā noņemt negatīvismu no sevis mājās: efektīvi veidi
Kā noņemt negatīvismu no sevis mājās: efektīvi veidi