Kõrvaliste juurte ilmnemise põhjused võrrandite lahendamisel. Töötuba "trigonomeetriliste võrrandite lahendamine". Võrrandite ekvivalentteisendused
Trigonomeetriliste võrrandite teema algab kooliloenguga, mis on üles ehitatud heuristilise vestluse vormis. Loengus käsitletakse teoreetilise materjali ja näiteid kõigi tüüpprobleemide lahendamisest vastavalt kavale:
- Lihtsamad trigonomeetrilised võrrandid.
- Trigonomeetriliste võrrandite lahendamise põhimeetodid.
- Homogeensed võrrandid.
Järgnevates tundides algab iseseisev oskuste arendamine, lähtudes õpetaja ja õpilase ühistegevuse põhimõtte rakendamisest. Esiteks seatakse õpilastele eesmärgid, s.t. määratakse kindlaks, kes ei taha teada rohkem, kui riigi standard nõuab, ja kes on valmis rohkem.
Lõplik diagnoos luuakse tasemete diferentseerumist arvestades, mis võimaldab õpilastel teadlikult määrata minimaalsed teadmised, mis on vajalikud hinde “3” saamiseks. Selle põhjal valitakse õpilaste teadmiste diagnoosimiseks mitmetasandilised materjalid. Selline töö võimaldab individuaalselt läheneda õpilastele, kaasates kõiki teadlikku õppetegevust, arendades eneseorganiseerumis- ja iseõppimisoskusi ning tagades ülemineku aktiivsele iseseisvale mõtlemisele.
Seminar viiakse läbi pärast trigonomeetriliste võrrandite lahendamise põhioskuste harjutamist. Mitu tundi enne seminari esitatakse õpilastele küsimusi, mida seminaril arutatakse.
Seminar koosneb kolmest osast.
1. Sissejuhatavas osas käsitletakse kogu teoreetiline materjal, sh sissejuhatus keeruliste võrrandite lahendamisel tekkivatesse probleemidesse.
2. Teises osas käsitletakse võrrandite lahendamist kujul:
- ja cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- võrrandid, mida saab lahendada astme vähendamise teel.
Need võrrandid kasutavad universaalset asendust, astme vähendamise valemeid ja abiargumendi meetodit.
3. Kolmandas osas käsitletakse juurekao ja kõrvaliste juurte omandamise probleeme. Näitab juurte valimist.
Õpilased töötavad rühmades. Näidete lahendamiseks kutsutakse hästi väljaõppinud tüübid, kes oskavad materjali näidata ja selgitada.
Seminar on mõeldud hästi ettevalmistatud üliõpilasele, sest... see käsitleb küsimusi, mis jäävad mõnevõrra programmi materjali ulatusest välja. See sisaldab keerukama kujuga võrrandeid ja käsitleb eelkõige keeruliste trigonomeetriliste võrrandite lahendamisel tekkinud probleeme.
Seminar toimus 10.–11. klassi õpilastele. Igal õpilasel oli võimalus oma teadmisi sel teemal laiendada ja süvendada, võrrelda oma teadmiste taset mitte ainult koolilõpetajale esitatavate nõuetega, vaid ka V.U.Z.-sse astujatele esitatavate nõuetega.
SEMINAR
Teema:"Trigonomeetriliste võrrandite lahendamine"
Eesmärgid:
- Üldistada teadmisi igat tüüpi trigonomeetriliste võrrandite lahendamisest.
- Keskenduge probleemidele: juurte kadu; kõrvalised juured; juure valik.
TUNNIDE AJAL.
I. Sissejuhatav osa
1. Trigonomeetriliste võrrandite lahendamise põhimeetodid
- Faktoriseerimine.
- Uue muutuja sissejuhatus.
- Funktsionaal-graafiline meetod.
2. Teatud tüüpi trigonomeetrilised võrrandid.
- Võrrandid, mis taandavad ruutvõrranditeks cos x = t, sin x = t suhtes.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Bsinx + C = 0.
Need lahendatakse uue muutuja sisseviimisega.
- Esimese ja teise astme homogeensed võrrandid
Esimese astme võrrand: Asinx + Bcosx = 0 jagades cos x-ga, saame Atg x + B = 0
Teise astme võrrand: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 jagage cos 2 x, saame Atg 2 x + Btgx + C = 0
Need lahendatakse faktoriseerimise ja uue muutuja sisseviimisega.
Kõik meetodid kehtivad.
- Mine alla versioonile:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Lahendatud faktoriseerimise meetodil.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Vormi võrrand: A(sinx + cosx) + Bsin2x + C = 0.
Taandatud ruuduks t = sinx + cosx suhtes; sin2x = t 2 – 1.
3. Valemid.
x + 2n; Kontrollimine on vajalik!
- Vähenev aste: cos 2 x = (1 + cos2x): 2; sin 2 x = (1 – cos 2x): 2
- Abiargumendi meetod.
Asendage Acosx + Bsinx Csiniga (x + ), kus sin = a/C; cos=v/c;
– abiargument.
4. Reeglid.
- Kui näete ruutu, langetage kraadi.
- Kui näete tükki, tehke summa.
- Kui näete summat, tehke tööd.
5. Juurte kadu, lisajuured.
- Juurte kadu: jagage g(x-ga); ohtlikud valemid (universaalne asendus). Nende toimingutega kitsendame definitsiooni ulatust.
- Lisajuured: tõstetud ühtlase võimsusega; korrutage g(x)-ga (vabanege nimetajast). Nende toimingutega laiendame definitsiooni ulatust.
II. Trigonomeetriliste võrrandite näited
1. Võrrandid kujul Asinx + Bcosx = C
1) Universaalne asendus.O.D.Z. x – ükskõik milline.
3 sin 2x + cos 2x + 1 = 0.
tgx = u. x/2 + n;
![]() u = – 1/3.
u = – 1/3.
tan x = –1/3, x = arctaan (–1/3) + k, k Z.
Eksam: 3sin( + 2n) + cos( + 2n) + 1= 3 sin + cos + 1 = 0 – 1 + 1 = 0.
x = /2 + n, n e Z. On võrrandi juur.
Vastus: x = arctaan(–1/3) + k, k Z. x = /2 + n, n Z.
2) Funktsionaal-graafiline meetod. O.D.Z. x – ükskõik milline.
Sinx – cosx = 1
Sinx = cosx + 1.
Joonistame funktsioonid: y = sinx, y = cosx + 1.

Vastus: x = /2 + 2 n, Z; x = + 2k, k Z.
3) Abiargumendi sissejuhatus. O.D.Z.: x – ükskõik milline.
8cosx + 15 sinx = 17.
![]()
8/17 cosx + 15/17 sinx = 1, sest (8/17) 2 + (15/17) 2 = 1, siis on olemas selline, et patt = 8/17,
cos = 15/17, mis tähendab sin cosx + sinx cos = 1; = arcsin 8/17.
Vastus: x = /2 + 2n – , x = /2 + 2n – arcsin 8/17, n Z.
2. Järjekorra vähendamine: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). sin 2 3x + sin 2 4x + sin 2 6x + sin 2 7x = 2. O.D.Z.: x – ükskõik milline.
1 - cos 6x + 1 - cos 8x + 1 - cos 12x + 1 - cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x (cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Vastus: x = /20 + n/10, n Z. x = /6 + k/3, k Z, x = /2 + m, m Z.
| Kell | k = 1 ja m = 0 k = 4 ja m = 1. |
sarjad on samad. |
3. Vähendamine homogeensuseni. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 3 sinx cosx + 6 cos 2 x = 5. ODZ: x – ükskõik milline.
5 sin 2 x + 3 sinx cosx + 6 cos 2 x – 5 sin 2 x – 5 cos 2 x = 0
3 sinxcosx + cos 2 x = 0 (1) ei saa jagada cos 2 x-ga, kuna kaotame juured.
cos 2 x = 0 rahuldab võrrandit.
cosx (3 sinx + cosx) = 0
cosx = 0. 3 sinx + cosx = 0.
x = /2 + k, k Z. tgx = –1/3, x = –/6 + n, n Z.
Vastus: x = /2 + k, k Z. , x = –/6 + n, n Z
4. Kuju võrrand: A(sinx + cosx) + B sin2x + C = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. O.D.Z.: x – ükskõik milline.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | <
2
2 t 2 – 5t + 2 = 0. t 1 = 2, t 2 = S.
sinx + cosx = S. cosx = sin(x + /2),
sinx + sin(x + /2) = 1/2,
2sin(x + /4) cos(–/4) = 1/2
sin(x + /4) = 1/22;
x +/4 = (–1) k arcsin(1/2 O 2) + k, k Z.
Vastus: x = (–1) k arcsin(1/22) – /4 + k, k Z.
5. Faktoriseerimine.
1) cos 2 x – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2) (cosx + 2 sinx) = 0.
1) cosx = 2, juurteta.
2) cosx + 2 sinx = 0
2tgx + 1 = 0
Vastus: x = arctaan(1/2) + n, n Z.
III. Trigonomeetriliste võrrandite lahendamisel tekkivad probleemid
1. Juurte kadu: jagage g(x-ga); Kasutame ohtlikke valemeid.
1) Leidke viga.
1 – cosx = sinx *sinx/2,
1 – cosx = 2sin 2 x/2 valem.
2 sin 2 x/2 = 2 sinx/2* сosx/2* sinx/2 jagage 2 sin 2 x/2,
1 = cosx/2
x/2 = 2n, x = 4n, n" Z.
Kaotatud juured sinx/2 = 0, x = 2k, k Z.
Õige lahendus: 2sin 2 x/2 (1 – cosx/2) = 0.
| sin 2 x/2 = 0 x = 2k, k Z. |
1 – cosx /2 = 0 x = 4p n, n Z. |
2. Võõrjuured: vabaneme nimetajast; tõsta ühtlase võimsuseni.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 3) = 0. O.D.Z.: sin2x 3/2.
2сos3х sinx – сos3x + 2sinx – 1 = 0
(cos3x + 1) (2sinx – 1) = 0
| 1). сos3x + 1 = 0 x = /3 + 2n/3, n Z. |
2). 2sinx – 1 = 0 x = (–1) k /6 + k, k Z. |

| I. x = /3 + 2n/3 1. n = 0 sin 2/3 = 3/2 ei rahulda. O.D.Z. 2. n = 1 3. n = 2 |
II. x = (–1) k /6 + k, k Z 1.k = 0 sin 2/6 = 3/2 ei rahulda O.D.Z. 2. k = 1 sin 2*5/6 = –3/2 rahuldada O.D.Z. |
Vastus: x = + 2k, x = 5/3 + 2k, x = 5/6 + 2k, k Z. t = 5 sin3x = 0
§ 1. KADUNUD JA VÄLJAVÕTETUD JUURED VÕRRANDITE LAHENDAMISEKS (NÄIDETEGA)
TUNNUSMATERJAL
1. VII peatüki § 3 kaks teoreemi rääkisid sellest, millised toimingud võrranditele ei riku nende samaväärsust.
2. Vaatleme nüüd selliseid tehteid võrranditega, mis võivad viia uue võrrandini, mis ei ole võrdne algse võrrandiga. Üldiste kaalutluste asemel piirdume vaid konkreetsete näidete käsitlemisega.
3. Näide 1. Antud on võrrand Avame selles võrrandis olevad sulud, nihutame kõik liikmed vasakule ja lahendame ruutvõrrandi. Selle juured on
Kui taandada võrrandi mõlemad pooled ühise teguriga, saadakse võrrand, mis on algse võrrandiga ebavõrdne, kuna sellel on ainult üks juur
Seega võib võrrandi mõlema poole vähendamine tundmatut sisaldava teguri võrra põhjustada võrrandi juurte kadumise.
4. Näide 2. Antud võrrand. Sellel võrrandil on üks juur. Tõstame selle võrrandi mõlemad pooled ruutu ja saame. Selle võrrandi lahendamisel leiame kaks juurt:
Näeme, et uus võrrand ei ole samaväärne algse võrrandiga. Juur on võrrandi juur, mis pärast mõlema poole ruudustamist viib võrrandini
5. Kõrvalised juured võivad ilmneda ka siis, kui võrrandi mõlemad pooled korrutatakse tundmatut sisaldava teguriga, kui see tegur kaob x reaalväärtuste korral.
Näide 3. Kui korrutame võrrandi mõlemad pooled sellega, saame uue võrrandi, mis pärast liikme paremalt küljelt vasakule ülekandmist ja faktoriseerimist annab võrrandi kummastki
Juur ei rahulda võrrandit, millel on ainult üks juur
Siit järeldame: võrrandi mõlema poole ruudustamisel (üldiselt ühtlase astmeni), samuti korrutamisel teguriga, mis sisaldab tundmatut ja kaob tundmatu tegelikel väärtustel, võivad ilmneda kõrvalised juured.
Kõik siin esitatud kaalutlused võrrandi kõrvaliste juurte kadumise ja ilmnemise kohta kehtivad võrdselt kõigi võrrandite (algebraline, trigonomeetriline jne) kohta.
6. Võrrandit nimetatakse algebraliseks, kui tundmatuga tehakse ainult algebralisi tehteid - liitmine, lahutamine, korrutamine, jagamine, astendamine ja juure lahutamine loomuliku astendajaga (ja selliste tehtete arv on lõplik).
Nii näiteks võrrandid

on algebralised ja võrrandid

HAMBAD. Selgroogsete hambad on ehituselt ja arengult täiesti sarnased haikalade kogu nahka katvate plakoidsete soomustega. Kuna kogu suuõõs ja osaliselt ka neeluõõs on vooderdatud ektodermaalse epiteeliga, on tüüpiline plakoid... ...
KOPSUTUBERKULOOS- KOPSUTUBERKULOOS. Sisu: I. Patoloogiline anatoomia.........110 II. Kopsutuberkuloosi klassifikatsioon... 124 III. Kliinik........................128 IV. Diagnostika..........................160 V. Prognoos................... ........ 190 VI. Ravi… Suur meditsiiniline entsüklopeedia
MÜRGISTUS- MÜRGISTUS. Mürgistus tähendab "looma funktsioonide häireid". organismid, mis on põhjustatud eksogeensetest või endogeensetest, keemiliselt või füüsikaliselt ja keemiliselt aktiivsetest ainetest, mis on kvaliteedi, koguse või kontsentratsiooni poolest võõrad... ... Suur meditsiiniline entsüklopeedia
Kaunviljade mügarbakterid- Paleontoloogilised andmed näitavad, et kõige iidsemad kaunviljad, millel olid mügarikud, olid mõned Eucaesalpinioideae rühma kuuluvad taimed. Kaasaegsetes liblikõielistes liikides on leitud mügar... Bioloogiline entsüklopeedia
Animasarja "Luntik" episoodide loend- Selles artiklis puuduvad lingid teabeallikatele. Teave peab olema kontrollitav, vastasel juhul võidakse see kahtluse alla seada ja kustutada. Saate... Wikipedia
TAIMED JA KESKKOND- Taime, nagu iga teise elusorganismi, elu on omavahel seotud protsesside kompleks; Kõige olulisem neist, nagu teada, on ainete vahetus keskkonnaga. Keskkond on allikas, kust...... Bioloogiline entsüklopeedia
Sarja "Luntik" episoodide loend- Põhiartikkel: Luntiku ja tema sõprade seiklused Sisukord 1 Episoodide arv 2 Animasarja Luntik ja tema sõbrad episoodide loend ... Wikipedia
Viljapuude haigused- Viljapuud peaksid tänu pidevale inimlikule hoolitsusele nende eest saama palju vanemaks kui nende kasvatamata sugulased, kui mitte paljude kultuuri enda tingimuste, nimelt meie poolt esitatud nõudmiste, vastumõjude tõttu... ...
Metsa raie- Metsa ülestöötamist ehk metsatulu väljavõtmist puidu ja puukoorena saab teha kahel viisil: kaevates või juurides välja terved puud, st tüved koos juurtega või eraldi, osade kaupa, esmalt raiudes või eemaldades. alates ... ... Entsüklopeediline sõnaraamat F.A. Brockhaus ja I.A. Efron
Grosh- (Poola grosz, saksa keelest Groschen, ladina keelest grossus (dēnārius) “paks denaarius”) erinevate maade ja aegade münt. Sisu 1 Senti välimus ... Wikipedia
USA mündid- 20 Saint Gaudensi dollarit kauneimad ja kallimad USA mündid USA mündid on USA rahapajas vermitud mündid. Toodetud aastast 1792... Wikipedia
Raamatud
- Naiste juuste väljalangemise peamised põhjused, Alexey Michman, Kuus naist kümnest kannatavad mingil eluperioodil juuste väljalangemise all. Juuste väljalangemine võib tekkida mitmel põhjusel, näiteks pärilikkus, hormonaalsed muutused... Kategooria:
Viimases tunnis kasutasime võrrandite lahendamiseks kolme sammu.
Esimene etapp on tehniline. Kasutades algse võrrandi teisenduste ahelat, jõuame üsna lihtsani, mille lahendame ja leiame juured.
Teine etapp on lahenduse analüüs. Analüüsime tehtud teisendusi ja selgitame välja, kas need on samaväärsed.
Kolmas etapp on kontrollimine. Kõigi leitud juurte kontrollimine, asendades need algsesse võrrandisse, on kohustuslik, kui sooritate teisendusi, mis võivad viia tagajärgvõrrandini
Kas võrrandi lahendamisel tuleb alati eristada kolme etappi?
Muidugi mitte. Nagu näiteks selle võrrandi lahendamisel. Igapäevaelus neid tavaliselt ei eristata. Kuid kõiki neid etappe tuleb "meeles pidada" ja ühel või teisel kujul läbi viia. On hädavajalik analüüsida teisenduste samaväärsust. Ja kui analüüs näitab, et kontrolli on vaja teha, siis on see kohustuslik. Vastasel juhul ei saa võrrandit lugeda õigesti lahendatuks.
Kas võrrandi juuri on alati võimalik kontrollida ainult asendamise teel?
Kui võrrandi lahendamisel kasutati samaväärseid teisendusi, siis kontrollimine pole vajalik. Võrrandi juurte kontrollimisel kasutatakse väga sageli ODZ-d (lubatud väärtuste vahemik), kui seda on ODZ abil raske kontrollida, siis asendatakse see algsesse võrrandisse.
1. harjutus
Lahendage võrrand ruutjuur kaks x pluss kolm võrdub üks pluss x.
Lahendus
Võrrandi ODZ määratakse kahe võrratuse süsteemiga: kaks x pluss kolm on suurem või võrdne nulliga ja üks pluss x on suurem või võrdne nulliga. Lahendus on x suurem kui miinus üks või sellega võrdne.
Teeme võrrandi mõlemad pooled ruudus, liigutame liikmed võrrandi ühelt küljelt teisele, lisame sarnased liikmed ja saame ruutvõrrandi x ruudus võrdub kahega. Selle juured on
x esimene, teine võrdub pluss või miinus ruutjuur kahest.
Läbivaatus
Väärtus x esimene on võrdne ruutjuurega kahest on võrrandi juur, kuna see sisaldub ODZ-s.
Väärtus x sekund võrdub miinus kahe ruutjuurega, ei ole võrrandi juur, sest see ei sisaldu DZ-s.
Kontrollime, et juur x on võrdne kahe ruutjuurega, asendades selle algsega, saame
võrdsus on tõene, mis tähendab, et x võrdub ruutjuurega kahest on võrrandi juur.
Vastus: ruutjuur kahest.
2. ülesanne
Lahendage võrrand ruutjuur x miinus kaheksa võrdub viis miinus x.
Lahendus
Irratsionaalvõrrandi ODZ määratakse kahe võrratuse süsteemiga: x miinus kaheksa on suurem või võrdne nulliga ja viis miinus x on suurem või võrdne nulliga. Seda lahendades leiame, et sellel süsteemil pole lahendusi. Võrrandi juur ei saa olla ükski muutuja x väärtustest.
Vastus: pole juuri.
3. ülesanne
Lahendage võrrand ruutjuur x kuup pluss neli x miinus üks miinus kaheksa ruutjuurt x neljas astmes miinus x võrdub ruutjuur x kuup miinus üks pluss kaks ruutjuurt x.
Lahendus
ODZ leidmine selles võrrandis on üsna keeruline.
Teostame teisenduse: ruudustage selle võrrandi mõlemad pooled,
Liigutame kõik liikmed võrrandist vasakule poole ja toome sarnased terminid, kirjutame ühe alla kaks juurt, saame sarnased radikaalid, toome sarnased, jagame koefitsiendiga miinus 12 ja korrutame radikaali avaldise, saame võrrandi kahe nulliga võrdse teguri korrutise kuju. Olles selle lahendanud, leiame juured:
x esimene on võrdne ühega, x teine on võrdne nulliga.
Kuna me tõstsime võrrandi mõlemad pooled ühtlase astmeni, on juurte kontrollimine kohustuslik.
Läbivaatus
Kui x on võrdne ühega, siis
saame õige võrdsuse, mis tähendab, et x võrdub ühega, on võrrandi juur.

Kui x on null, on miinus ühe ruutjuur määratlemata.
See tähendab, et x võrdne nulliga on kõrvaline juur.
Vastus: üks.
4. ülesanne
Lahendage avaldise x ruudus pluss viis x pluss kaks põhikaks võrrandi logaritm võrdub kolmega.
Lahendus
Leiame ODZ võrrandi. Selleks lahendame võrratuse x ruudus pluss viis x pluss kaks üle nulli.
Lahendame ebavõrdsuse intervallmeetodi abil. Selleks faktoriseerime selle vasaku külje, olles eelnevalt ruutvõrrandi lahendanud, ja võttes arvesse ebavõrdsuse märki, määrame ODZ. ODZ on võrdne avatud kiirte ühendusega miinus lõpmatusest miinus murdarvuni viis pluss seitsmeteistkümne ruutjuur jagatud kahega ning miinus murdarvust viis miinus seitsmeteistkümne ruutjuur jagatud kahega pluss lõpmatuseni.
Nüüd hakkame leidma võrrandi juuri. Arvestades, et kolm on võrdne logaritmiga kaheksast aluse kahele, kirjutame võrrandi järgmiselt: avaldise x ruut pluss viis x pluss kaks kahe aluse logaritmiga võrdub kaheksa logaritmiga kahe põhi. Potentseerime võrrandit, saame ja lahendame ruutvõrrandi.
Diskriminant on nelikümmend üheksa.
Arvutage juured:
x esimene on võrdne miinus kuus; x sekund on võrdne ühega.
Läbivaatus
Miinus kuus kuulub ODZ-i, üks kuulub ODZ-i, mis tähendab, et mõlemad arvud on võrrandi juured.
Vastus: miinus kuus; üks.
Viimases tunnis käsitlesime kõrvaliste juurte väljanägemise küsimust. Saame need tuvastada kontrollimise teel. Kas võrrandi lahendamisel on võimalik kaotada juuri ja kuidas seda vältida?
Kui sooritate võrrandiga selliseid toiminguid, nagu esiteks võrrandi mõlema poole jagamine sama avaldisega ax x-st (välja arvatud juhud, kui on kindlalt teada, et x-st tulenev ax ei ole võrdne nulliga ühegi x-i korral võrrandi määratluspiirkond) ;
teiseks võib võrrandi OD kitsendamine lahendusprotsessi käigus kaasa tuua võrrandi juurte kadumise.
Pea meeles!

Võrrand, mis on kirjutatud kujul
ef x-ist korrutatud tuhaga x-st on võrdne zhe-ga x-st korrutatud tuhaga x-st lahendatakse järgmiselt:
peate faktoriseerima, jättes ühisteguri sulgudest välja;
seejärel võrdsustage iga tegur nulliga, saades seeläbi kaks võrrandit.
Arvutame nende juured.
1. harjutus
Lahendage võrrand x kuup võrdub x-ga.
Esimene viis
Jagage selle võrrandi mõlemad pooled x-ga, saame x ruut võrdub ühega, mille juured x on kõigepealt üks,
x sekund võrdub miinus ühega.
Teine viis
X kuup võrdub X-ga. Liigutame x võrrandi vasakule poole, võtame sulgudest välja x ja saame: x korrutatuna x ruuduga miinus üks võrdub nulliga.
Arvutame selle juured:
X esimene on võrdne nulliga, x teine on võrdne ühega, x kolmas on võrdne miinus ühega.
Võrrandil on kolm juurt.
Esimese meetodi lahendamisel kaotasime ühe juure - x võrdub nulliga.
Vastus: miinus üks; null; üks.
Pea meeles! Võrrandi mõlema poole vähendamine tundmatut sisaldava teguri võrra võib põhjustada juurte kadumise.
2. ülesanne
Lahendage võrrand: x kümnendlogaritm ruudus on võrdne kahega.
Lahendus
Esimene viis
Logaritmi definitsiooni järgi saame ruutvõrrandi x ruut võrdub sajaga.
Selle juured: x esimene võrdub kümnega; X sekund võrdub miinus kümnega.
Teine viis
Logaritmide omaduse järgi on meil kaks kümnendlogaritmi x võrdub kahega.
Selle juur - x on võrdne kümnega

Teise meetodi korral on juur x võrdne miinus kümnega. Ja põhjus on selles, et nad rakendasid vale valemit, ahendades võrrandi ulatust. X ruudu kümnendlogaritmi avaldis on defineeritud kõigi x jaoks, välja arvatud x, mis on võrdne nulliga. X kümnendlogaritmi avaldis on x jaoks suurem kui null. Kümnendlogaritmi x ruut õige valem on võrdne kahe kümnendlogaritmi mooduliga x.
Pea meeles! Võrrandi lahendamisel kasuta olemasolevaid valemeid targalt.
Põhilised võrrandite lahendamise meetodid
Mis on võrrandi lahendus?
Identne teisendus. Põhiline
identiteedi transformatsioonide tüübid.
Võõrjuur. Juure kaotus.
Võrrandi lahendamine on protsess, mis seisneb peamiselt antud võrrandi asendamises teise võrrandiga, mis on sellega samaväärne . Seda asendust nimetatakseidentne teisendus . Peamised identiteedimuutused on järgmised:
1.
Ühe avaldise asendamine teisega, mis on sellega identselt võrdne. Näiteks võrrand (3 x+ 2 ) 2 = 15 x+ 10 võib asendada järgmise ekvivalendiga:9 x 2 + 12 x+ 4 = 15 x+ 10 .
2.
Võrrandiliikmete ülekandmine ühelt küljelt teisele pöördmärkidega. Seega saame eelmises võrrandis kõik selle tingimused paremalt küljelt vasakule märgiga “-” üle kanda: 9 x 2 + 12 x+ 4 – 15 x – 10 = 0, mille järel saame:9 x 2 – 3 x – 6 = 0 .
3.
Võrrandi mõlema poole korrutamine või jagamine sama avaldise (arvuga), mis ei ole null. See on väga oluline, sestuus võrrand ei pruugi olla samaväärne eelmisega, kui avaldis, millega korrutame või jagame, võib olla võrdne nulliga.
NÄIDE Võrrandx – 1 = 0 on ühe juuregax = 1.
Mõlema külje korrutaminex – 3 , saame võrrandi
( x – 1)( x – 3) = 0, millel on kaks juurt:x = 1 jax = 3.
Viimane väärtus ei ole antud võrrandi juur
x – 1 = 0. See on nnkõrvaline juur .
Jaotus võib vastupidi kaasa tuuajuurte kadu . Niisiis
meie puhul, kui (x – 1 )( x – 3 ) = 0 on originaal
võrrand, seejärel juurx = 3 kaotatakse jagamisel
võrrandi mõlemad pooled sissex – 3 .
Viimases võrrandis (punkt 2) saame kõik selle liikmed jagada 3-ga (mitte nulliga!) ja lõpuks saada:
3 x 2 – x – 2 = 0 .
See võrrand on samaväärne algse võrrandiga:
(3 x+ 2) 2 = 15 x+ 10 .
4.
Saabtõsta võrrandi mõlemad pooled paaritu astmeni võieraldage võrrandi mõlemalt küljelt paaritu juur . Tuleb meeles pidada, et:
a) ehitus sisseühtlane aste võib põhjustadavõõraste juurte omandamisele ;
b)vale kaevandamineisegi juur võib kaasa tuuajuurte kaotus .
NÄITED. Võrrand 7x = 35 on üks juurx = 5 .
Selle võrrandi mõlema poole ruudustamisel saame
võrrand:
49 x 2 = 1225 .
millel on kaks juurt:x = 5 Jax = – 5. Viimane väärtus
on kõrvaline juur.
Vale võttes mõlema ruutjuure
võrrandi 49 osadx 2 = 1225 tulemust 7x = 35,
ja me kaotame oma juuredx = – 5.
Õige võttes tulemuseks ruutjuure
võrrand: | 7x | = 35, A seega kahel juhul:
1) 7 x = 35, Siisx = 5 ; 2) – 7 x = 35, Siisx = – 5 .
Seetõttu, millalõige väljavõte ruut
juurtest me ei kaota võrrandi juuri.
Mida tähendabÕige ekstrakti juur? See on koht, kus me kohtume
väga olulise kontseptsioonigaaritmeetiline juur
(cm. ).
 Manikhas Georgi Moiseevitši elulugu
Manikhas Georgi Moiseevitši elulugu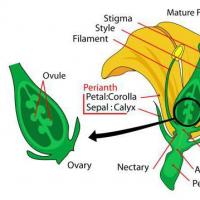 Botaanika on taimeteaduse haru
Botaanika on taimeteaduse haru Kõige tõhusam hommikune meditatsioon, näpunäited, kuidas hommikul mediteerida
Kõige tõhusam hommikune meditatsioon, näpunäited, kuidas hommikul mediteerida Kuidas kasutatakse seitsme kiriku vett?
Kuidas kasutatakse seitsme kiriku vett? Koguduse kahjude eemaldamine: Issanda vägi päästab teid tugevast needusest
Koguduse kahjude eemaldamine: Issanda vägi päästab teid tugevast needusest Kuidas eemaldada endalt kodus negatiivsust: tõhusad viisid
Kuidas eemaldada endalt kodus negatiivsust: tõhusad viisid