Milline transformatsioon ei too kaasa juurte kadumist. Võrrandite teisendus, ekvivalentteisendused. Vastavalt DL-i tingimustele
Trigonomeetriliste võrrandite teema algab kooliloenguga, mis on üles ehitatud heuristilise vestluse vormis. Loengus käsitletakse teoreetilise materjali ja näiteid kõigi tüüpprobleemide lahendamisest vastavalt kavale:
- Lihtsamad trigonomeetrilised võrrandid.
- Trigonomeetriliste võrrandite lahendamise põhimeetodid.
- Homogeensed võrrandid.
Järgnevates tundides algab iseseisev oskuste arendamine, lähtudes õpetaja ja õpilase ühistegevuse põhimõtte rakendamisest. Esiteks seatakse õpilastele eesmärgid, s.t. määratakse kindlaks, kes ei taha teada rohkem, kui riigi standard nõuab, ja kes on valmis rohkem.
Lõplik diagnoos luuakse tasemete diferentseerumist arvestades, mis võimaldab õpilastel teadlikult määrata minimaalsed teadmised, mis on vajalikud hinde “3” saamiseks. Selle põhjal valitakse õpilaste teadmiste diagnoosimiseks mitmetasandilised materjalid. Selline töö võimaldab individuaalselt läheneda õpilastele, kaasates kõiki teadlikku õppetegevust, arendades eneseorganiseerumis- ja iseõppimisoskusi ning tagades ülemineku aktiivsele iseseisvale mõtlemisele.
Seminar viiakse läbi pärast trigonomeetriliste võrrandite lahendamise põhioskuste harjutamist. Mitu tundi enne seminari esitatakse õpilastele küsimusi, mida seminaril arutatakse.
Seminar koosneb kolmest osast.
1. Sissejuhatavas osas käsitletakse kogu teoreetiline materjal, sh sissejuhatus keeruliste võrrandite lahendamisel tekkivatesse probleemidesse.
2. Teises osas käsitletakse võrrandite lahendamist kujul:
- ja cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- võrrandid, mida saab lahendada astme vähendamise teel.
Need võrrandid kasutavad universaalset asendust, astme vähendamise valemeid ja abiargumendi meetodit.
3. Kolmandas osas käsitletakse juurte kadumise ja kõrvaliste juurte omandamise probleeme. Näitab juurte valimist.
Õpilased töötavad rühmades. Näidete lahendamiseks kutsutakse hästi väljaõppinud tüübid, kes oskavad materjali näidata ja selgitada.
Seminar on mõeldud hästi ettevalmistatud üliõpilasele, sest... see käsitleb küsimusi, mis jäävad mõnevõrra programmi materjali ulatusest välja. See sisaldab keerukama kujuga võrrandeid ja käsitleb eelkõige keeruliste trigonomeetriliste võrrandite lahendamisel tekkinud probleeme.
Seminar toimus 10.–11. klassi õpilastele. Igal õpilasel oli võimalus oma teadmisi sel teemal laiendada ja süvendada, võrrelda oma teadmiste taset mitte ainult koolilõpetajale esitatavate nõuetega, vaid ka V.U.Z.-sse astujatele esitatavate nõuetega.
SEMINAR
Teema:"Trigonomeetriliste võrrandite lahendamine"
Eesmärgid:
- Üldistada teadmisi igat tüüpi trigonomeetriliste võrrandite lahendamisest.
- Keskenduge probleemidele: juurte kadu; kõrvalised juured; juure valik.
TUNNIDE AJAL.
I. Sissejuhatav osa
1. Trigonomeetriliste võrrandite lahendamise põhimeetodid
- Faktoriseerimine.
- Uue muutuja sissejuhatus.
- Funktsionaal-graafiline meetod.
2. Teatud tüüpi trigonomeetrilised võrrandid.
- Võrrandid, mis taandavad ruutvõrranditeks cos x = t, sin x = t suhtes.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Bsinx + C = 0.
Need lahendatakse uue muutuja sisseviimisega.
- Esimese ja teise astme homogeensed võrrandid
Esimese astme võrrand: Asinx + Bcosx = 0 jagades cos x-ga, saame Atg x + B = 0
Teise astme võrrand: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 jagage cos 2 x, saame Atg 2 x + Btgx + C = 0
Need lahendatakse faktoriseerimise ja uue muutuja sisseviimisega.
Kõik meetodid kehtivad.
- Mine alla versioonile:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Lahendatud faktoriseerimise meetodil.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Vormi võrrand: A(sinx + cosx) + Bsin2x + C = 0.
Taandatud ruuduks t = sinx + cosx suhtes; sin2x = t 2 – 1.
3. Valemid.
x + 2n; Kontrollimine on vajalik!
- Vähenev aste: cos 2 x = (1 + cos2x): 2; sin 2 x = (1 – cos 2x): 2
- Abiargumendi meetod.
Asendage Acosx + Bsinx Csiniga (x + ), kus sin = a/C; cos=v/c;
– abiargument.
4. Reeglid.
- Kui näete ruutu, langetage kraadi.
- Kui näete tükki, tehke summa.
- Kui näete summat, tehke tööd.
5. Juurte kadu, lisajuured.
- Juurte kadu: jagage g(x-ga); ohtlikud valemid (universaalne asendus). Nende toimingutega kitsendame definitsiooni ulatust.
- Lisajuured: tõstetud ühtlase võimsusega; korrutage g(x)-ga (vabanege nimetajast). Nende toimingutega laiendame definitsiooni ulatust.
II. Trigonomeetriliste võrrandite näited
1. Võrrandid kujul Asinx + Bcosx = C
1) Universaalne asendus.O.D.Z. x – ükskõik milline.
3 sin 2x + cos 2x + 1 = 0.
tgx = u. x/2 + n;
![]() u = – 1/3.
u = – 1/3.
tan x = –1/3, x = arctaan (–1/3) + k, k Z.
Eksam: 3sin( + 2n) + cos( + 2n) + 1= 3 sin + cos + 1 = 0 – 1 + 1 = 0.
x = /2 + n, n e Z. On võrrandi juur.
Vastus: x = arctaan(–1/3) + k, k Z. x = /2 + n, n Z.
2) Funktsionaal-graafiline meetod. O.D.Z. x – ükskõik milline.
Sinx – cosx = 1
Sinx = cosx + 1.
Joonistame funktsioonid: y = sinx, y = cosx + 1.

Vastus: x = /2 + 2 n, Z; x = + 2k, k Z.
3) Abiargumendi sissejuhatus. O.D.Z.: x – ükskõik milline.
8cosx + 15 sinx = 17.
![]()
8/17 cosx + 15/17 sinx = 1, sest (8/17) 2 + (15/17) 2 = 1, siis on olemas selline, et patt = 8/17,
cos = 15/17, mis tähendab sin cosx + sinx cos = 1; = arcsin 8/17.
Vastus: x = /2 + 2n – , x = /2 + 2n – arcsin 8/17, n Z.
2. Järjekorra vähendamine: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). sin 2 3x + sin 2 4x + sin 2 6x + sin 2 7x = 2. O.D.Z.: x – ükskõik milline.
1 - cos 6x + 1 - cos 8x + 1 - cos 12x + 1 - cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x (cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Vastus: x = /20 + n/10, n Z. x = /6 + k/3, k Z, x = /2 + m, m Z.
| Kell | k = 1 ja m = 0 k = 4 ja m = 1. |
sarjad on samad. |
3. Vähendamine homogeensuseni. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 3 sinx cosx + 6 cos 2 x = 5. ODZ: x – ükskõik milline.
5 sin 2 x + 3 sinx cosx + 6 cos 2 x – 5 sin 2 x – 5 cos 2 x = 0
3 sinxcosx + cos 2 x = 0 (1) ei saa jagada cos 2 x-ga, kuna kaotame juured.
cos 2 x = 0 rahuldab võrrandit.
cosx (3 sinx + cosx) = 0
cosx = 0. 3 sinx + cosx = 0.
x = /2 + k, k Z. tgx = –1/3, x = –/6 + n, n Z.
Vastus: x = /2 + k, k Z. , x = –/6 + n, n Z
4. Kuju võrrand: A(sinx + cosx) + B sin2x + C = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. O.D.Z.: x – ükskõik milline.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | <
2
2 t 2 – 5t + 2 = 0. t 1 = 2, t 2 = S.
sinx + cosx = S. cosx = sin(x + /2),
sinx + sin(x + /2) = 1/2,
2sin(x + /4) cos(–/4) = 1/2
sin(x + /4) = 1/22;
x +/4 = (–1) k arcsin(1/2 O 2) + k, k Z.
Vastus: x = (–1) k arcsin(1/22) – /4 + k, k Z.
5. Faktoriseerimine.
1) cos 2 x – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2) (cosx + 2 sinx) = 0.
1) cosx = 2, juurteta.
2) cosx + 2 sinx = 0
2tgx + 1 = 0
Vastus: x = arctaan(1/2) + n, n Z.
III. Trigonomeetriliste võrrandite lahendamisel tekkivad probleemid
1. Juurte kadu: jagage g(x-ga); Kasutame ohtlikke valemeid.
1) Leidke viga.
1 – cosx = sinx *sinx/2,
1 – cosx = 2sin 2 x/2 valem.
2 sin 2 x/2 = 2 sinx/2* сosx/2* sinx/2 jagage 2 sin 2 x/2,
1 = cosx/2
x/2 = 2n, x = 4n, n" Z.
Kaotatud juured sinx/2 = 0, x = 2k, k Z.
Õige lahendus: 2sin 2 x/2 (1 – cosx/2) = 0.
| sin 2 x/2 = 0 x = 2k, k Z. |
1 – cosx /2 = 0 x = 4p n, n Z. |
2. Võõrjuured: vabaneme nimetajast; tõsta ühtlase võimsuseni.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 3) = 0. O.D.Z.: sin2x 3/2.
2сos3х sinx – сos3x + 2sinx – 1 = 0
(cos3x + 1) (2sinx – 1) = 0
| 1). сos3x + 1 = 0 x = /3 + 2n/3, n Z. |
2). 2sinx – 1 = 0 x = (–1) k /6 + k, k Z. |

| I. x = /3 + 2n/3 1. n = 0 sin 2/3 = 3/2 ei rahulda. O.D.Z. 2. n = 1 3. n = 2 |
II. x = (–1) k /6 + k, k Z 1.k = 0 sin 2/6 = 3/2 ei rahulda O.D.Z. 2. k = 1 sin 2*5/6 = –3/2 rahuldada O.D.Z. |
Vastus: x = + 2k, x = 5/3 + 2k, x = 5/6 + 2k, k Z. t = 5 sin3x = 0
Põhilised võrrandite lahendamise meetodid
Mis on võrrandi lahendus?
Identne teisendus. Põhiline
identiteedi transformatsioonide tüübid.
Võõrjuur. Juure kaotus.
Võrrandi lahendamine on protsess, mis seisneb peamiselt antud võrrandi asendamises teise võrrandiga, mis on sellega samaväärne . Seda asendust nimetatakseidentne teisendus . Peamised identiteedimuutused on järgmised:
1.
Ühe avaldise asendamine teisega, mis on sellega identselt võrdne. Näiteks võrrand (3 x+ 2 ) 2 = 15 x+ 10 võib asendada järgmise ekvivalendiga:9 x 2 + 12 x+ 4 = 15 x+ 10 .
2.
Võrrandiliikmete ülekandmine ühelt küljelt teisele pöördmärkidega. Seega saame eelmises võrrandis kõik selle tingimused paremalt küljelt vasakule "-" märgiga üle kanda: 9 x 2 + 12 x+ 4 – 15 x – 10 = 0, mille järel saame:9 x 2 – 3 x – 6 = 0 .
3.
Võrrandi mõlema poole korrutamine või jagamine sama avaldise (arvuga), mis ei ole null. See on väga oluline, sestuus võrrand ei pruugi olla samaväärne eelmisega, kui avaldis, millega korrutame või jagame, võib olla võrdne nulliga.
NÄIDE Võrrandx – 1 = 0 on ühe juuregax = 1.
Mõlema külje korrutaminex – 3 , saame võrrandi
( x – 1)( x – 3) = 0, millel on kaks juurt:x = 1 jax = 3.
Viimane väärtus ei ole antud võrrandi juur
x – 1 = 0. See on nnkõrvaline juur .
Jaotus võib vastupidi kaasa tuuajuurte kadu . Niisiis
meie puhul, kui (x – 1 )( x – 3 ) = 0 on originaal
võrrand, seejärel juurx = 3 kaotatakse jagamisel
võrrandi mõlemad pooled sissex – 3 .
Viimases võrrandis (punkt 2) saame kõik selle liikmed jagada 3-ga (mitte nulliga!) ja lõpuks saada:
3 x 2 – x – 2 = 0 .
See võrrand on samaväärne algse võrrandiga:
(3 x+ 2) 2 = 15 x+ 10 .
4.
Saabtõsta võrrandi mõlemad pooled paaritu astmeni võieraldage võrrandi mõlemalt küljelt paaritu juur . Tuleb meeles pidada, et:
a) ehitus sisseühtlane aste võib põhjustadavõõraste juurte omandamisele ;
b)vale kaevandamineisegi juur võib kaasa tuuajuurte kaotus .
NÄITED. Võrrand 7x = 35 on üks juurx = 5 .
Selle võrrandi mõlema poole ruudustamisel saame
võrrand:
49 x 2 = 1225 .
millel on kaks juurt:x = 5 Jax = – 5. Viimane väärtus
on kõrvaline juur.
Vale võttes mõlema ruutjuure
võrrandi 49 osadx 2 = 1225 tulemust 7x = 35,
ja me kaotame oma juuredx = – 5.
Õige võttes tulemuseks ruutjuure
võrrand: | 7x | = 35, A seega kahel juhul:
1) 7 x = 35, Siisx = 5 ; 2) – 7 x = 35, Siisx = – 5 .
Seetõttu, millalõige väljavõte ruut
juurtest me ei kaota võrrandi juuri.
Mida tähendabÕige ekstrakti juur? See on koht, kus me kohtume
väga olulise kontseptsioonigaaritmeetiline juur
(cm. ).
Võib põhjustada nn kõrvaliste juurte ilmumist. Selles artiklis analüüsime kõigepealt üksikasjalikult, mis on kõrvalised juured. Teiseks räägime nende esinemise põhjustest. Ja kolmandaks vaatleme näidete abil peamisi meetodeid kõrvaliste juurte välja filtreerimiseks, see tähendab juurte kontrollimist, et nende hulgas oleks kõrvalisi, et need vastusest välja jätta.
Võrrandi kõrvaljuured, definitsioon, näited
Kooli algebra õpikud ei anna kõrvalise juure definitsiooni. Seal moodustatakse kõrvalise juure idee, kirjeldades järgmist olukorda: võrrandi mõne teisenduse abil tehakse üleminek algvõrrandilt järelvõrrandile, leitakse saadud kaasvõrrandi juured. , ja leitud juuri kontrollitakse asendades algsesse võrrandisse, mis näitab, et osa leitud juurtest ei ole algvõrrandi juured, neid juuri nimetatakse algvõrrandi kõrvalisteks juurteks.
Sellest alusest lähtudes võite enda jaoks nõustuda järgmise kõrvalise juure määratlusega:
Definitsioon
Kõrvalised juured- need on teisenduste tulemusel saadud tagajärgvõrrandi juured, mis ei ole algvõrrandi juured.
Toome näite. Vaatleme võrrandit ja selle võrrandi x·(x−1)=0 tagajärge, mis saadakse avaldise asendamisel identselt võrdse avaldisega x·(x−1) . Algsel võrrandil on üks juur 1. Teisenduse tulemusel saadud võrrandil on kaks juurt 0 ja 1. See tähendab, et 0 on algse võrrandi kõrvaline juur.
Võõrjuurte võimaliku ilmumise põhjused
Kui järelvõrrandi saamiseks ei kasutata "eksootilisi" teisendusi, vaid kasutatakse võrrandite põhiteisendusi, siis võivad kõrvalised juured tekkida ainult kahel põhjusel:
- ODZ laienemise tõttu ja
- võrrandi mõlema poole tõstmise tõttu samale paarisastmele.
Siinkohal tasub meenutada, et ODZ laienemine võrrandi teisendamise tulemusena toimub peamiselt
- Fraktsioonide vähendamisel;
- Toote asendamisel ühe või mitme nullteguriga nulliga;
- Nulliga murdosa asendamisel lugeja nulliga;
- Kasutades mõningaid astmete, juurte, logaritmide omadusi;
- Mõne trigonomeetrilise valemi kasutamisel;
- Kui võrrandi mõlemad pooled korrutatakse sama avaldisega, kaob see selle võrrandi ODZ võrra;
- Lahendusprotsessis logaritmimärkidest vabastamisel.
Näide artikli eelmisest lõigust illustreerib kõrvalise juure tekkimist ODZ laienemise tõttu, mis tekib võrrandilt kaasvõrrandile üleminekul x·(x−1)=0. Algse võrrandi ODZ on kõigi reaalarvude hulk, välja arvatud null, saadud võrrandi ODZ on hulk R, see tähendab, et ODZ-d laiendatakse arvuga null. See arv osutub lõpuks kõrvaliseks juureks.
Toome ka näite kõrvalise juure ilmnemisest võrrandi mõlema poole tõstmise tõttu samale paarisastmele. Irratsionaalsel võrrandil on üks juur 4 ja selle võrrandi tagajärg, mis saadakse võrrandi mõlema poole ruudustamisel, see tähendab võrrandil ![]() , on kaks juurt 1 ja 4. Sellest on selge, et võrrandi mõlema poole ruudu kandmine tõi kaasa algse võrrandi kõrvalise juure.
, on kaks juurt 1 ja 4. Sellest on selge, et võrrandi mõlema poole ruudu kandmine tõi kaasa algse võrrandi kõrvalise juure.
Pange tähele, et ODZ laiendamine ja võrrandi mõlema poole tõstmine samale ühtlasele võimsusele ei too alati kaasa kõrvaliste juurte ilmnemist. Näiteks võrrandilt järelvõrrandile x=2 liikudes laieneb ODZ kõigi mittenegatiivsete arvude hulgast kõigi reaalarvude hulka, kuid kõrvalisi juuri ei ilmu. 2 on nii esimese kui ka teise võrrandi ainus juur. Samuti ei ilmu võrrandilt järelvõrrandile liikudes kõrvalisi juuri. Nii esimese kui ka teise võrrandi ainus juur on x=16. Seetõttu ei räägi me kõrvaliste juurte ilmnemise põhjustest, vaid võõrjuurte võimaliku ilmnemise põhjustest.
Mis on kõrvaliste juurte väljasõelumine?
Mõistet “kõrvaljuurte väljasõelumine” saab nimetada ainult venitusega, seda ei leidu kõigis algebraõpikutes, kuid see on intuitiivne, mistõttu seda tavaliselt kasutatakse. Mida mõeldakse kõrvaliste juurte väljasõelumise all, selgub järgmisest lausest: „... kontrollimine on võrrandi lahendamise kohustuslik samm, mis aitab tuvastada kõrvalisi juuri, kui neid on, ja need ära visata (tavaliselt öeldakse: „rooki välja ”)."
Seega
Definitsioon
Kõrvaliste juurte väljasõelumine- see on kõrvaliste juurte tuvastamine ja kõrvaldamine.
Nüüd saate liikuda kõrvaliste juurte väljasõelumise meetodite juurde.
Meetodid kõrvaliste juurte väljasõelumiseks
Asenduskontroll
Peamine viis kõrvaliste juurte välja filtreerimiseks on asendustest. See võimaldab teil välja juurida kõrvalised juured, mis võivad tekkida nii ODZ laienemise kui ka võrrandi mõlema poole tõstmise tõttu samale ühtlasele võimsusele.
Asendustest on järgmine: järelvõrrandi leitud juured asendatakse omakorda algvõrrandiga või sellega samaväärse võrrandiga, need, mis annavad õige arvulise võrrandi, on algvõrrandi juured ja need, mis annavad vale numbriline võrdus või avaldis on algvõrrandi juured.mõttetu, on algvõrrandi kõrvalised juured.
Näitame näitega, kuidas filtreerida välja kõrvalised juured, asendades algsesse võrrandisse.
Mõnel juhul on otstarbekam kõrvalised juured välja filtreerida muude meetoditega. See kehtib peamiselt nende juhtumite kohta, kui asendusega kontrollimine on seotud oluliste arvutusraskustega või kui teatud tüüpi võrrandite lahendamise standardmeetod nõuab teist kontrolli (näiteks murruratsionaalvõrrandite lahendamisel kõrvaliste juurte väljasõelumine toimub vastavalt tingimusel, et murru nimetaja ei ole võrdne nulliga ). Vaatame alternatiivseid viise kõrvaliste juurte väljarookimiseks.
DL andmetel
Erinevalt asendustestimisest ei ole kõrvaliste juurte filtreerimine ODZ abil alati asjakohane. Fakt on see, et see meetod võimaldab teil välja filtreerida ainult ODZ laienemise tõttu tekkivad kõrvalised juured ja see ei garanteeri kõrvaliste juurte väljasõelumist, mis võivad tekkida muudel põhjustel, näiteks mõlema poole tõstmise tõttu. võrrandist sama paarisvõimsusega . Pealegi ei ole lahendatava võrrandi OD-i alati lihtne leida. Sellegipoolest tasub ODZ-i abil võõraste juurte väljasõelumise meetodit kasutada, kuna selle kasutamine nõuab sageli vähem arvutustööd kui muude meetodite kasutamine.
Kõrvaliste juurte väljarookimine vastavalt ODZ-le toimub järgmiselt: kõiki leitud järelvõrrandi juuri kontrollitakse, kas need kuuluvad algvõrrandi või sellega võrdväärse võrrandi muutuja lubatud väärtuste vahemikku, need, mis kuuluvad ODZ-i, on algvõrrandi juured ja need, mis kuuluvad ODZ-sse, on algvõrrandi juured ja need, mis ei kuulu ODZ-i, on algse võrrandi kõrvalised juured.
Esitatud teabe analüüs viib järeldusele, et ODZ-i abil on soovitatav välja sõeluda kõrvalised juured, kui samal ajal:
- algse võrrandi ODZ-i on lihtne leida,
- kõrvalised juured võivad tekkida ainult ODZ laienemise tõttu,
- Asendustestimine on seotud märkimisväärsete arvutusraskustega.
Näitame, kuidas võõraste juurte välja rookimine praktikas toimub.
Vastavalt DL-i tingimustele
Nagu eelmises lõigus ütlesime, kui kõrvalised juured võivad tekkida ainult ODZ laienemise tõttu, saab need kõrvaldada, kasutades algse võrrandi ODZ-d. Kuid ODZ-i numbrilise komplekti kujul pole alati lihtne leida. Sellistel juhtudel on võimalik kõrvalisi juuri välja sõeluda mitte ODZ, vaid ODZ määravate tingimuste järgi. Selgitame, kuidas ODZ tingimustes võõraste juurte välja rookimine toimub.
Leitud juured asendatakse omakorda tingimustega, mis määravad ODZ algse võrrandi või sellega võrdväärse võrrandi jaoks. Need, mis vastavad kõigile tingimustele, on võrrandi juured. Ja need, mis ei vasta vähemalt ühele tingimusele või annavad avaldise, millel pole mõtet, on algse võrrandi kõrvalised juured.
Toome näite kõrvaliste juurte väljasõelumisest vastavalt ODZ tingimustele.
Kõrvaliste juurte väljarookimine, mis tulenevad võrrandi mõlema poole tõstmisest ühtlase võimsuseni
On selge, et kõrvaliste juurte väljarookimine, mis tulenevad võrrandi mõlema poole tõstmisest samale võrdsele astmele, saab teha asendades selle algsesse võrrandisse või mis tahes sellega samaväärsesse võrrandisse. Kuid selline kontroll võib kaasa tuua märkimisväärseid arvutusraskusi. Sel juhul tasub teada alternatiivset meetodit kõrvaliste juurte väljasõelumiseks, millest me nüüd räägime.
Kõrvaliste juurte väljasõelumine, mis võivad tekkida vormi irratsionaalsete võrrandite mõlema poole tõstmisel samale paarisastmele ![]() , kus n on mõni paarisarv, saab teostada vastavalt tingimusele g(x)≥0. See tuleneb paarisastme juure definitsioonist: paarisastme juur n on mittenegatiivne arv, mille n-s aste võrdub radikaalarvuga, kust
, kus n on mõni paarisarv, saab teostada vastavalt tingimusele g(x)≥0. See tuleneb paarisastme juure definitsioonist: paarisastme juur n on mittenegatiivne arv, mille n-s aste võrdub radikaalarvuga, kust  . Seega on kõlanud lähenemine omamoodi sümbioos võrrandi mõlema poole samale astmele tõstmise meetodist ja irratsionaalsete võrrandite lahendamise meetodist juure määramise teel. See tähendab, võrrand
. Seega on kõlanud lähenemine omamoodi sümbioos võrrandi mõlema poole samale astmele tõstmise meetodist ja irratsionaalsete võrrandite lahendamise meetodist juure määramise teel. See tähendab, võrrand ![]() , kus n on paarisarv, lahendatakse võrrandi mõlema poole tõstmisega samale paarisastmele ja kõrvaliste juurte elimineerimine toimub vastavalt tingimusele g(x)≥0, mis on võetud irratsionaalsete võrrandite lahendamise meetodist juure määramine.
, kus n on paarisarv, lahendatakse võrrandi mõlema poole tõstmisega samale paarisastmele ja kõrvaliste juurte elimineerimine toimub vastavalt tingimusele g(x)≥0, mis on võetud irratsionaalsete võrrandite lahendamise meetodist juure määramine.
Viimases tunnis kasutasime võrrandite lahendamiseks kolme sammu.
Esimene etapp on tehniline. Kasutades algse võrrandi teisenduste ahelat, jõuame üsna lihtsani, mille lahendame ja leiame juured.
Teine etapp on lahenduse analüüs. Analüüsime tehtud teisendusi ja selgitame välja, kas need on samaväärsed.
Kolmas etapp on kontrollimine. Kõigi leitud juurte kontrollimine, asendades need algsesse võrrandisse, on kohustuslik, kui sooritate teisendusi, mis võivad viia tagajärgvõrrandini
Kas võrrandi lahendamisel tuleb alati eristada kolme etappi?
Muidugi mitte. Nagu näiteks selle võrrandi lahendamisel. Igapäevaelus neid tavaliselt ei eristata. Kuid kõiki neid etappe tuleb "meeles pidada" ja ühel või teisel kujul läbi viia. On hädavajalik analüüsida teisenduste samaväärsust. Ja kui analüüs näitab, et kontrolli on vaja teha, siis on see kohustuslik. Vastasel juhul ei saa võrrandit lugeda õigesti lahendatuks.
Kas võrrandi juuri on alati võimalik kontrollida ainult asendamise teel?
Kui võrrandi lahendamisel kasutati samaväärseid teisendusi, siis kontrollimine pole vajalik. Võrrandi juurte kontrollimisel kasutatakse väga sageli ODZ-d (lubatud väärtuste vahemik), kui seda on ODZ abil raske kontrollida, siis asendatakse see algsesse võrrandisse.
1. harjutus
Lahendage võrrand ruutjuur kaks x pluss kolm võrdub üks pluss x.
Lahendus
Võrrandi ODZ määratakse kahe võrratuse süsteemiga: kaks x pluss kolm on suurem või võrdne nulliga ja üks pluss x on suurem või võrdne nulliga. Lahendus on x suurem kui miinus üks või sellega võrdne.
Teeme võrrandi mõlemad pooled ruudus, liigutame liikmed võrrandi ühelt küljelt teisele, lisame sarnased liikmed ja saame ruutvõrrandi x ruudus võrdub kahega. Selle juured on
x esimene, teine võrdub pluss või miinus ruutjuur kahest.
Uurimine
Väärtus x esimene on võrdne ruutjuurega kahest on võrrandi juur, kuna see sisaldub ODZ-s.
Väärtus x sekund võrdub miinus kahe ruutjuurega, ei ole võrrandi juur, sest see ei sisaldu DZ-s.
Kontrollime, et juur x on võrdne kahe ruutjuurega, asendades selle algsega, saame
võrdsus on tõene, mis tähendab, et x võrdub ruutjuurega kahest on võrrandi juur.
Vastus: ruutjuur kahest.
2. ülesanne
Lahendage võrrand ruutjuur x miinus kaheksa võrdub viis miinus x.
Lahendus
Irratsionaalvõrrandi ODZ määratakse kahe võrratuse süsteemiga: x miinus kaheksa on suurem või võrdne nulliga ja viis miinus x on suurem või võrdne nulliga. Seda lahendades leiame, et sellel süsteemil pole lahendusi. Võrrandi juur ei saa olla ükski muutuja x väärtustest.
Vastus: pole juuri.
3. ülesanne
Lahendage võrrand ruutjuur x kuup pluss neli x miinus üks miinus kaheksa ruutjuurt x neljas astmes miinus x võrdub ruutjuur x kuup miinus üks pluss kaks ruutjuurt x.
Lahendus
ODZ leidmine selles võrrandis on üsna keeruline.
Teostame teisenduse: ruudustage selle võrrandi mõlemad pooled,
Liigutame kõik liikmed võrrandist vasakule poole ja toome sarnased terminid, kirjutame ühe alla kaks juurt, saame sarnased radikaalid, toome sarnased, jagame koefitsiendiga miinus 12 ja korrutame radikaali avaldise, saame võrrandi kahe nulliga võrdse teguri korrutise kuju. Olles selle lahendanud, leiame juured:
x esimene on võrdne ühega, x teine on võrdne nulliga.
Kuna me tõstsime võrrandi mõlemad pooled ühtlase astmeni, on juurte kontrollimine kohustuslik.
Uurimine
Kui x on võrdne ühega, siis
saame õige võrdsuse, mis tähendab, et x võrdub ühega, on võrrandi juur.

Kui x on null, on miinus ühe ruutjuur määratlemata.
See tähendab, et x võrdne nulliga on kõrvaline juur.
Vastus: üks.
4. ülesanne
Lahendage avaldise x ruudus pluss viis x pluss kaks põhikaks võrrandi logaritm võrdub kolmega.
Lahendus
Leiame ODZ võrrandi. Selleks lahendame võrratuse x ruudus pluss viis x pluss kaks üle nulli.
Lahendame ebavõrdsuse intervallmeetodi abil. Selleks faktoriseerime selle vasaku külje, olles eelnevalt ruutvõrrandi lahendanud, ja võttes arvesse ebavõrdsuse märki, määrame ODZ. ODZ on võrdne avatud kiirte ühendusega miinus lõpmatusest miinus murdarvuni viis pluss seitsmeteistkümne ruutjuur jagatud kahega ning miinus murdarvust viis miinus seitsmeteistkümne ruutjuur jagatud kahega pluss lõpmatuseni.
Nüüd hakkame leidma võrrandi juuri. Arvestades, et kolm on võrdne logaritmiga kaheksast aluse kahele, kirjutame võrrandi järgmiselt: avaldise x ruut pluss viis x pluss kaks kahe aluse logaritmiga võrdub kaheksa logaritmiga kahe põhi. Potentseerime võrrandit, saame ja lahendame ruutvõrrandi.
Diskriminant on nelikümmend üheksa.
Arvutage juured:
x esimene on võrdne miinus kuus; x sekund on võrdne ühega.
Uurimine
Miinus kuus kuulub ODZ-i, üks kuulub ODZ-i, mis tähendab, et mõlemad arvud on võrrandi juured.
Vastus: miinus kuus; üks.
Viimases tunnis käsitlesime kõrvaliste juurte väljanägemise küsimust. Saame need tuvastada kontrollimise teel. Kas võrrandi lahendamisel on võimalik kaotada juuri ja kuidas seda vältida?
Kui sooritate võrrandiga selliseid toiminguid, nagu esiteks võrrandi mõlema poole jagamine sama avaldisega ax x-st (välja arvatud juhud, kui on kindlalt teada, et x-st tulenev ax ei ole võrdne nulliga ühegi x-i korral võrrandi määratluspiirkond) ;
teiseks võib võrrandi OD kitsendamine lahendusprotsessi käigus kaasa tuua võrrandi juurte kadumise.
Pea meeles!

Võrrand, mis on kirjutatud kujul
ef x-ist korrutatud tuhaga x-st on võrdne zhe-ga x-st korrutatud tuhaga x-st lahendatakse järgmiselt:
peate faktoriseerima, jättes ühisteguri sulgudest välja;
seejärel võrdsustage iga tegur nulliga, saades seeläbi kaks võrrandit.
Arvutame nende juured.
1. harjutus
Lahendage võrrand x kuup võrdub x-ga.
Esimene viis
Jagage selle võrrandi mõlemad pooled x-ga, saame x ruut võrdub ühega, mille juured x on kõigepealt üks,
x sekund võrdub miinus ühega.
Teine viis
X kuup võrdub X-ga. Liigutame x võrrandi vasakule poole, võtame sulgudest välja x ja saame: x korrutatuna x ruuduga miinus üks võrdub nulliga.
Arvutame selle juured:
X esimene on võrdne nulliga, x teine on võrdne ühega, x kolmas on võrdne miinus ühega.
Võrrandil on kolm juurt.
Esimese meetodi lahendamisel kaotasime ühe juure - x võrdub nulliga.
Vastus: miinus üks; null; üks.
Pea meeles! Võrrandi mõlema poole vähendamine tundmatut sisaldava teguri võrra võib põhjustada juurte kadumise.
2. ülesanne
Lahendage võrrand: x kümnendlogaritm ruudus on võrdne kahega.
Lahendus
Esimene viis
Logaritmi definitsiooni järgi saame ruutvõrrandi x ruut võrdub sajaga.
Selle juured: x esimene võrdub kümnega; X sekund võrdub miinus kümnega.
Teine viis
Logaritmide omaduse järgi on meil kaks kümnendlogaritmi x võrdub kahega.
Selle juur - x on võrdne kümnega

Teise meetodi korral on juur x võrdne miinus kümnega. Ja põhjus on selles, et nad rakendasid vale valemit, ahendades võrrandi ulatust. X ruudu kümnendlogaritmi avaldis on defineeritud kõigi x jaoks, välja arvatud x, mis on võrdne nulliga. X kümnendlogaritmi avaldis on x jaoks suurem kui null. Kümnendlogaritmi x ruut õige valem on võrdne kahe kümnendlogaritmi mooduliga x.
Pea meeles! Võrrandi lahendamisel kasuta olemasolevaid valemeid targalt.
Juurte ja kõrvaliste juurte kadu võrrandite lahendamisel
Munitsipaalõppeasutus "Üksikute ainete süvaõppega keskkool nr 2" Vsevolozhski linnas. Uurimistöö koostas 11. B klassi õpilane: Vassiljev Vassili. Projektijuht: Egorova Ljudmila Alekseevna.
Võrrand Esiteks vaatame erinevaid viise selle võrrandi lahendamiseks sinx+cosx =- 1
Lahendus nr 1 sinx+cosx =-1 i Y x 0 1 sin(x+)=- 1 sin(x+)=- x+ =- +2 x+ = +2 + x=- +2 x= +2 Vastus: + 2
Lahendus nr 2 sinx+cosx =- 1 i Vastus: +2 y x 0 1 2sin cos + - + + = 0 sin cos + = 0 cos (cos + sin)= 0 cos =0 cos + sin =1 = + m tg =-1 = + m =- + x=- +2 x= +2
Lahendus nr 3 I y x 0 1 sinx+cosx =- 1 2 = x= x+ x sin2x=0 2x= x= Vastus:
sinx+cosx =-1 Lahendus nr 4 i y x 0 1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n Vastus: - + 2 n
Võrdleme lahendusi Õiged lahendused Mõelgem välja, millistel juhtudel võivad tekkida kõrvalised juured ja miks nr 2 Vastus: +2 nr 3 Vastus: nr 4 Vastus: + 2 n nr 1 Vastus: +2
Lahenduse kontrollimine Kas on vaja kontrollida? Kas peaksin kindluse mõttes juured igaks juhuks üle kontrollima? See on muidugi kasulik, kui seda on lihtne asendada, kuid matemaatikud on ratsionaalsed inimesed ega tee tarbetuid asju. Vaatame erinevaid juhtumeid ja pidage meeles, millal on kontrollimine tõesti vajalik.
1. Lihtsamad valmisvalemid c osx =a x=a =a s inx =a t gx =a Juhtudel, kui juured leitakse kõige lihtsamate valmisvalemite abil, ei pea kontrolli tegema. Selliseid valemeid kasutades tuleks aga meeles pidada, millistel tingimustel saab neid kasutada. Näiteks valemit = saab kasutada tingimusel a 0, -4ac 0 Ja vastust x= arccos2+2 võrrandile cosx =2 peetakse jämeks veaks, kuna valem x= arccos a +2 saab olla ainult kasutatakse võrrandi cosx =a juurte jaoks, kus | a | 1
2. Teisendused Sagedamini tuleb võrrandite lahendamisel läbi viia palju teisendusi. Kui võrrand asendatakse uuega, millel on kõik eelmise juured, ja see teisendatakse nii, et juurte kadu või omandamist ei toimu, siis nimetatakse selliseid võrrandeid ekvivalentseteks. 1. Võrrandi komponentide ühest osast teise ülekandmisel. 2. Kui lisate mõlemale poolele sama numbri. 3. Kui võrrandi mõlemad pooled korrutatakse sama nullist erineva arvuga. 4 . Identiteetide rakendamisel, mis kehtivad kõigi reaalarvude hulgal. Kontrollimine pole aga vajalik!
Siiski ei saa iga võrrandit lahendada samaväärsete teisendustega. Sagedamini on vaja rakendada ebavõrdseid teisendusi. Sageli põhinevad sellised teisendused valemite kasutamisel, mis ei kehti kõigi reaalväärtuste puhul. Sel juhul muutub eelkõige võrrandi määratluspiirkond. See viga leitakse lahenduses nr 4. Vaatame viga, aga kõigepealt vaatame uuesti lahendust nr 4. sinx+cosx=-1 + =-1 2tg +1- =-1- 2tg =-2 =- + n x = - + 2 n Viga peitub valemis sin2x= Seda valemit võib kasutada, kuid tuleks lisaks kontrollida kas juured on arvud kujul +, mille puhul tg pole defineeritud. Nüüd on selge, et lahendus on juurte kadu. Vaatame selle lõpuni.
Lahendus nr 4 i y x 0 1 Kontrollime arve = + n asendusega: x= + 2 n sin(+ 2 n)+ cos (+ 2 n)=sin + cos =0+(-1)=- 1 Nii et x= +2 n on võrrandi juur Vastus: +2 sinx+cosx =-1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n
Vaatasime ühte juurte kaotamise viisidest, matemaatikas on neid palju, nii et peate hoolikalt lahendama, pidades meeles kõiki reegleid. Nii nagu võite kaotada võrrandi juured, saate selle lahendamise käigus ka juurde hankida. Vaatleme lahendust nr 3, milles selline viga tehti.
Lahendus nr 3 I y x 0 1 2 2 ja lisajuured! Kõrvalised juured võivad ilmneda, kui võrrandi mõlemad pooled olid ruudus. Sel juhul on vaja kontrollida. Kui n=2k on meil sin k+cos k=-1; cos k=-1 kui k=2m-1 , Siis n=2(2m+1)=4m+2 , x= = +2 m , Vastus: +2 Kui n=2k+1 on meil sin +cos =- 1 sin(+ k)+ cos (+ k)=- 1 cos k-sin k=- 1 cos k=-1, kus k=2m+1 n=2(2m+1)+ 1=2m+3 x= (4m+3)= +2 m=- +2 sinx+cosx =- 1 = x= x+ x sin2x=0 2x= x=
Niisiis, vaatlesime paari võimalikku juhtumit, mida on väga palju. Püüdke mitte raisata oma aega ja teha rumalaid vigu.
 Manikhas Georgi Moiseevitši elulugu
Manikhas Georgi Moiseevitši elulugu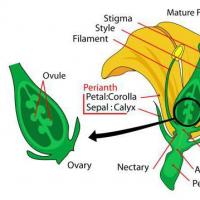 Botaanika on taimeteaduse haru
Botaanika on taimeteaduse haru Kõige tõhusam hommikune meditatsioon, näpunäited, kuidas hommikul mediteerida
Kõige tõhusam hommikune meditatsioon, näpunäited, kuidas hommikul mediteerida Kuidas kasutatakse seitsme kiriku vett?
Kuidas kasutatakse seitsme kiriku vett? Koguduse kahjude eemaldamine: Issanda vägi päästab teid tugevast needusest
Koguduse kahjude eemaldamine: Issanda vägi päästab teid tugevast needusest Kuidas eemaldada endalt kodus negatiivsust: tõhusad viisid
Kuidas eemaldada endalt kodus negatiivsust: tõhusad viisid