Što su brojčani sustavi? Mali fakultet matematike. Pretvaranje razlomaka decimalnog sustava u bilo koji drugi
Notacija je metoda pisanja broja pomoću određenog skupa posebnih znakova (znamenki).
Notacija:
- daje prikaz skupa brojeva (cijelih i/ili realnih);
- daje svakom broju jedinstveni prikaz (ili barem standardni prikaz);
- prikazuje algebarsku i aritmetičku strukturu broja.
Zapisivanje broja u nekom brojevnom sustavu naziva se brojčani kod.
Poziva se posebna pozicija u prikazu broja pražnjenje, što znači da je broj pozicije rang broj.
Broj znamenki u broju naziva se dubina bita a podudara se s njegovom dužinom.
Brojevni sustavi dijele se na pozicijski I nepozicijski. Pozicijski brojevni sustavi su podijeljeni
na homogena I mješoviti.
oktalni brojevni sustav, heksadekadski brojevni sustav i drugi brojevni sustavi.
Prijevod brojevnih sustava. Brojevi se mogu pretvarati iz jednog brojevnog sustava u drugi.
Tablica korespondencije brojeva u različitim brojevnim sustavima.
Postoje položajni i nepozicijski brojčani sustavi.
U nepozicijskim brojevnim sustavima težina znamenke (tj. doprinos koji daje vrijednosti broja) ne ovisi o njenom položaju u pisanju broja. Dakle, u rimskom brojevnom sustavu u broju XXXII (trideset dva), težina broja X na bilo kojoj poziciji je jednostavno deset.
U položajnim brojevnim sustavima težina svake znamenke varira ovisno o njezinoj poziciji (poziciji) u nizu znamenki koje predstavljaju broj. Na primjer, u broju 757,7 prvih sedam znači 7 stotica, drugo - 7 jedinica, a treće - 7 desetina jedinice.
Sam zapis broja 757,7 znači skraćeni zapis izraza
700 + 50 + 7 + 0,7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757,7.
Svaki položajni brojevni sustav karakterizira njegov osnova.
Za osnovu sustava može se uzeti bilo koji prirodni broj - dva, tri, četiri itd. Stoga, mogući bezbrojni položajni sustavi: binarni, ternarni, kvaternarni itd. Zapisivanje brojeva u svakom brojevnom sustavu s osnovom q znači skraćeni izraz
a n-1 q n-1 +a n-2 q n-2 + ... + a 1 q 1 +a 0 q 0 +a -1 q -1 + ... +a -m q -m ,
Gdje a ja - brojevi brojevnog sustava; n I m - broj cijelih i razlomljenih znamenki. Na primjer:
Koje brojčane sustave koriste stručnjaci za komunikaciju s računalom?
Osim decimalnih, naširoko se koriste sustavi s bazom koja je cjelobrojna potencija broja 2, naime:
binarni(koriste se znamenke 0, 1);
oktalni(koriste se znamenke 0, 1, ..., 7);
heksadecimalni(za prve cijele brojeve od nula do devet koriste se znamenke 0, 1, ..., 9, a za sljedeće brojeve - od deset do petnaest - koriste se simboli A, B, C, D, E, F kao znamenke).
Korisno je zapamtiti zapis u ovim brojevnim sustavima za prve dvije desetice cijelih brojeva:
|
|
|
Od svih brojevnih sustava posebno jednostavno i stoga Binarni brojevni sustav zanimljiv je za tehničku implementaciju u računalima.
Što je brojevni sustav?
Što je brojevni sustav? Brojevni sustav je skup tehnika i pravila po kojima se brojevi pišu i čitaju.
Postoje položajni i nepozicijski brojčani sustavi.
U nepozicijskim brojevnim sustavima težina znamenke (tj. doprinos koji daje vrijednosti broja) ne ovisi o njezinu položaju u zapisu broja. Dakle, u rimskom brojevnom sustavu u broju XXXII (trideset dva), težina broja X na bilo kojoj poziciji je jednostavno deset.
U pozicijskim brojevnim sustavima težina svake znamenke varira ovisno o njezinu položaju (poziciji) u nizu znamenki koje predstavljaju broj. Na primjer, u broju 757,7 prvih sedam znači 7 stotica, drugo - 7 jedinica, a treće - 7 desetina jedinice.
Sam zapis broja 757,7 znači skraćeni zapis izraza:
Svaki položajni sustav brojeva karakterizira njegova baza.
Osnova pozicijskog brojevnog sustava je broj različitih znamenki koje se koriste za predstavljanje brojeva u određenom brojevnom sustavu.
Za osnovu sustava može se uzeti bilo koji prirodni broj - dva, tri, četiri itd. Posljedično, moguć je beskonačan broj položajnih sustava: binarni, ternarni, kvaternarni itd.
Kako se generiraju cijeli brojevi u pozicijskim brojevnim sustavima?
U svakom brojevnom sustavu znamenke su poredane prema značenju: 1 je veće od 0, 2 je veće od 1 itd.
Promicanje znamenke odnosi se na njezinu zamjenu sljedećom najvećom.
Napredovati broj 1 znači zamijeniti ga s 2, unaprijediti broj 2 znači zamijeniti ga s 3 itd. Promicanje vodeće znamenke (na primjer, broj 9 u decimalnom sustavu) znači njezinu zamjenu s 0. U binarnom sustavu, koji koristi samo dvije znamenke - 0 i 1, promicanje 0 znači njezinu zamjenu s 1, a promicanje 1 znači zamjenu s 0.
Da bi se formirao cijeli broj nakon bilo kojeg danog cijelog broja, krajnja desna znamenka broja mora biti pomaknuta naprijed; ako bilo koja znamenka postane nula nakon promicanja, tada morate unaprijediti znamenku lijevo od nje.
Primjenjujući ovo pravilo, zapisujemo prvih deset cijelih brojeva
· u binarnom sustavu: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
· u trojnom sustavu: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
· u peterostrukom sustavu: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
· u oktalnom sustavu: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Osim decimalnih, naširoko se koriste sustavi s bazom koja je cjelobrojna potencija broja 2, naime:
| Binarni sustav | Kvartarni sustav | Oktalni sustav | Dekadski sustav | Heksadecimalni sustav |
| 1 | 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 | 3 |
| 100 | 10 | 4 | 4 | 4 |
| 101 | 11 | 5 | 5 | 5 |
| 110 | 12 | 6 | 6 | 6 |
| 111 | 13 | 7 | 7 | 7 |
| 1000 | 20 | 10 | 8 | 8 |
| 1001 | 21 | 11 | 9 | 9 |
| 1010 | 22 | 12 | 10 | A |
| 1011 | 23 | 13 | 11 | B |
| 1100 | 30 | 14 | 12 | C |
| 1101 | 31 | 15 | 13 | D |
| 1110 | 32 | 16 | 14 | E |
| 1111 | 33 | 17 | 15 | F |
| 10000 | 40 | 20 | 16 | 10 |
Ljudi više vole decimalni sustav vjerojatno zato što se od davnina broji na prste, a ljudi imaju deset prstiju na rukama i nogama. Ljudi ne koriste uvijek i ne svugdje decimalni brojevni sustav. U Kini su, primjerice, dugo koristili peteroznamenkasti sustav brojeva.
A računala koriste binarni sustav jer ima niz prednosti u odnosu na druge sustave:
· za njegovu provedbu potrebni su nam tehnički uređaji s dva stabilna stanja (ima struje - nema struje, magnetizirano - nije magnetizirano itd.), a ne npr. s deset, kao u decimali;
· prikaz informacija kroz samo dva stanja je pouzdan i otporan na smetnje;
· moguće je koristiti aparat Booleove algebre za izvođenje logičkih transformacija informacija;
· Binarna aritmetika mnogo je jednostavnija od decimalne aritmetike.
Nedostatak binarnog sustava je brzo povećanje broja znamenki potrebnih za zapis brojeva.
Zašto računala također koriste oktalni i heksadecimalni brojevni sustav?
Binarni sustav, pogodan za računala, nezgodan je za ljude zbog svoje glomaznosti i neobičnog zapisa.
Pretvorbu brojeva iz decimalnog sustava u binarni sustav i obrnuto obavlja stroj. Međutim, da biste profesionalno koristili računalo, morate naučiti razumjeti riječ stroj. Zbog toga su razvijeni oktalni i heksadecimalni sustavi.
Brojevi u tim sustavima gotovo su lako čitljivi kao i decimalni; oni zahtijevaju tri (oktalno) odnosno četiri (heksadecimalno) puta manje znamenki nego u binarnom sustavu (uostalom, brojevi 8 i 16 su redom treća i četvrta potencija broja 2) .
Pretvaranje brojeva iz jednog brojevnog sustava u drugi
Broj p različitih znamenki koji se koristi u položajnom sustavu određuje naziv brojevnog sustava i naziva se baza brojevnog sustava - "p". Svaki broj N u pozicijskom brojevnom sustavu s bazom p može se prikazati kao polinom s bazom p:
N = a n p n +a n-1 p n-1 + ... +a 1 p+a 0 +a -1 p -1 +a -2 p -2 + ... (1.1)
ovdje je N broj, a j su koeficijenti (znamenke broja), p je baza brojevnog sustava (p>1). Uobičajeno je predstavljati brojeve kao niz znamenki:
N = a n a n -1 ... a 1 a 0 . a -1 a -2 ...
Pretvorba brojeva u decimalni sustav provodi se sastavljanjem potencijskog niza s bazom sustava (vidi formulu 1.1) iz kojeg se broj pretvara. Zatim se izračunava vrijednost zbroja.
|
|
|
|
Pretvorba cijelih decimalnih brojeva u nedecimalni brojevni sustav provodi se sekvencijskim dijeljenjem decimalnog broja s bazom sustava u koji se pretvara dok se ne dobije kvocijent te baze. Broj se u novom sustavu zapisuje kao ostatak dijeljenja, počevši od zadnjeg.
Primjer: Pretvorimo broj 75 iz decimalnog u binarni, oktalni i heksadecimalni:

Odgovor: 75 10 = 1 001 011 2 = 113 8 = 4B 16.
Pretvaranje pravih razlomaka iz decimalnog brojevnog sustava u nedekadski brojevni sustav. Za pretvaranje regularnog decimalnog razlomka u drugi sustav, ovaj se razlomak mora uzastopno pomnožiti s bazom sustava u koji se pretvara. U ovom slučaju množe se samo razlomački dijelovi. Razlomci se u novom sustavu pišu u obliku cijelih dijelova proizvoda, počevši od prvog.
Primjer. Pretvorimo broj 0,36 iz decimalnog sustava u binarni, oktalni i heksadecimalni:

Da biste pretvorili nepravilni decimalni razlomak u brojevni sustav s nedecimalnom bazom, morate odvojeno pretvoriti cijeli dio i odvojeno razlomak. Prevedi 23.125 10 2 s.s.
Brojevni sustavi se nazivaju višestrukim ako vrijedi odnos: S = R N, gdje su S, R baze brojevnih sustava, N je stupanj višestrukosti (cijeli broj: 2, 3 ...).
Da biste pretvorili broj iz brojevnog sustava R u njegov višestruki brojevni sustav S, postupite na sljedeći način: krećući se od točke lijevo i desno, dijele broj u skupine od N znamenki, dopunjujući krajnju lijevu i krajnju desnu skupinu nulama, ako potrebno. Grupa se tada zamjenjuje odgovarajućom znamenkom iz S brojevnog sustava.
| Prijevod 1101111001.1101 2 "8" s.s. | Prijevod 11111111011.100111 2 "16" s.c. |
Za prevođenje broja iz brojevnog sustava S u njegov višestruki brojevni sustav R dovoljno je svaku znamenku tog broja zamijeniti odgovarajućim brojem iz brojevnog sustava R, a beznačajne nule u visokom (00512) i niskom (15,124000) znamenke se odbacuju.
| Prevedi 305.4 8 "2" s.s. | Prevedite 7B2.E 16 "2" s.s. |
|
|
Ako trebate pretvoriti iz brojevnog sustava S u R, pod uvjetom da nisu višekratnici, tada morate pokušati odabrati brojevni sustav K tako da je: S = K N i R = K N .
Prevedi 175.24 8 "16" s.s.
Rezultat: 175.24 8 = 7D.5 16.
Ako se brojevni sustav K ne može pronaći, tada treba izvršiti prevođenje koristeći decimalni brojevni sustav kao posrednik.
Primjeri za sve ovo
Pretvaranje oktalnih i heksadecimalnih brojeva u binarni sustav vrlo je jednostavno: dovoljno je svaku znamenku zamijeniti odgovarajućom binarnom trijadom (tri znamenke) ili tetradom (četiri znamenke).
Na primjer:
Da biste broj pretvorili iz binarnog u oktalni ili heksadecimalni, trebate ga razdvojiti lijevo i desno od decimalne točke na trijade (za oktalni) ili tetrade (za heksadecimalni) i zamijeniti svaku takvu skupinu odgovarajućom oktalnom (heksadecimalnom) znamenkom . Na primjer:

Zbrajanje u raznim brojevnim sustavima
Tablice zbrajanja lako je izraditi pomoću pravila brojanja.






Oduzimanje u raznim brojevnim sustavima

Množenje u različitim brojevnim sustavima
Prilikom množenja višeznamenkastih brojeva u različitim položajnim brojevnim sustavima, možete koristiti uobičajeni algoritam za množenje brojeva u stupcu, ali rezultati množenja i zbrajanja jednoznamenkastih brojeva moraju se posuditi iz tablica množenja i zbrajanja koje odgovaraju sustavu u pitanje.



Dijeljenje u različitim brojevnim sustavima
Dijeljenje u bilo kojem položajnom brojevnom sustavu provodi se prema istim pravilima kao i dijeljenje kutom u decimalnom sustavu. U binarnom sustavu dijeljenje je posebno jednostavno, jer sljedeća znamenka količnika može biti samo nula ili jedinica.
Množite s bazom novog brojevnog sustava sve dok novi razlomak ne bude imao potreban broj znamenki, koji je određen potrebnom točnošću prikaza razlomka. Pravi razlomak u novom brojevnom sustavu piše se iz cjelobrojnih dijelova umnožaka nastalih uzastopnim množenjem, a prvi cjelobrojni dio bit će najveća znamenka novog razlomka. Uzmimo primjer...

Prikazi u njima su prilično veliki brojevi, jer to rezultira izuzetno glomaznim zapisom brojeva ili zahtijeva vrlo veliku abecedu brojeva. Računala koriste samo položajne brojčane sustave, u kojima kvantitativni ekvivalent svake znamenke abecede ne ovisi samo o vrsti te znamenke, već i o njezinom položaju u zapisu broja. Pozicijski brojevni sustavi...





Nizovi 0 i 1. Na primjer, nenegativan cijeli broj A2=T 111100002 bit će pohranjen u ćeliju na sljedeći način: 1 1 1 1 0 0 0 0 To znači da sve brojeve od 0 do 255 možemo zapisati u binarnom obliku brojevni sustav u 1 memorijskoj ćeliji. 2.2 Predstavljanje brojeva u računalu Cijeli brojevi u računalu pohranjeni su u memorijskim ćelijama, u ovom slučaju svaka znamenka memorijske ćelije odgovara...
Predstavljanje brojeva pisanim simbolima.
Notacija:
- daje prikaze skupa brojeva (cijelih i/ili realnih);
- daje svakom broju jedinstveni prikaz (ili barem standardni prikaz);
- odražava algebarsku i aritmetičku strukturu brojeva.
Brojevni sustavi dijele se na pozicijski, nepozicijski I mješoviti.
Pozicijski brojevni sustavi
U položajnim brojevnim sustavima isti brojčani znak (znamenka) u zapisu broja ima različito značenje ovisno o mjestu (znamenki) na kojem se nalazi. Izum položajnog numeriranja, temeljenog na mjesnom značenju znamenki, pripisuje se Sumeranima i Babiloncima; Takvo numeriranje razvili su Hindusi i imalo je neprocjenjive posljedice u povijesti ljudske civilizacije. Takvi sustavi uključuju moderni decimalni brojevni sustav, čiji je nastanak povezan s brojanjem na prste. Pojavio se u srednjovjekovnoj Europi preko talijanskih trgovaca, koji su ga pak posudili od muslimana.
Pozicijski brojevni sustav obično se odnosi na -bogati brojevni sustav, koji je određen cijelim brojem tzv osnova brojevni sustavi. Cijeli broj bez predznaka u -arnom brojevnom sustavu predstavlja se kao konačna linearna kombinacija potencija broja:
, gdje su cijeli brojevi tzv u brojkama, zadovoljavajući nejednakost.Svaki stupanj u takvoj notaciji naziva se težina ranga. Seniornost znamenki i njima odgovarajućih znamenki određena je vrijednošću pokazatelja (broj znamenki). Tipično, u brojevima koji nisu nula, lijeve nule su izostavljene.
Ako nema odstupanja (na primjer, kada su svi brojevi predstavljeni u obliku jedinstvenih pisanih znakova), broj je napisan kao niz njegovih alfanumeričkih znamenki, navedenih prema silaznom redoslijedu prednosti znamenki s lijeva na desno:
Na primjer, broj sto tri predstavljen u decimalnom brojevnom sustavu kao:
Trenutno najčešće korišteni položajni sustavi su:
U položajnim sustavima, što je baza sustava veća, to je manji broj znamenki (tj. pisanih znamenki) potreban za pisanje broja.
Mješoviti brojevni sustavi
Mješoviti brojevni sustav je generalizacija bogatog brojevnog sustava i često se odnosi na položajne brojevne sustave. Osnova mješovitog brojevnog sustava je rastući niz brojeva, a svaki broj u njemu predstavljen je kao linearna kombinacija:
, gdje se koeficijenti nazivaju kao i prije u brojkama vrijede neka ograničenja.Zapisivanje broja u mješovitom brojevnom sustavu je ispisivanje njegovih znamenki silaznim redoslijedom indeksa, počevši od prve koja nije nula.
Ovisno o vrsti kao funkciji, mješoviti brojevni sustavi mogu biti potencijski, eksponencijalni itd. Kada se za neke, mješoviti brojevni sustav podudara s eksponencijalno bogatim brojevnim sustavom.
Najpoznatiji primjer mješovitog brojevnog sustava je prikaz vremena kao broja dana, sati, minuta i sekundi. U ovom slučaju, vrijednost "dani, sati, minute, sekunde" odgovara vrijednosti sekundi.
Faktorski brojevni sustav
U faktorski brojevni sustav baze su niz faktorijela, a svaki prirodni broj je predstavljen kao:
, Gdje .Faktorijalni brojevni sustav koristi se kada dekodiranje permutacija listama inverzija: imajući broj permutacije, možete ga reproducirati na sljedeći način: broj koji je za jedan manji od broja (numeriranje počinje od nule) zapisuje se u faktorijalnom brojevnom sustavu, a koeficijent broja i! označit će broj inverzija za element i+1 u skupu u kojem su napravljene permutacije (broj elemenata manji od i+1, ali koji se nalaze desno od njega u željenoj permutaciji)
Primjer: razmotrite skup permutacija od 5 elemenata, ima ih ukupno 5! = 120 (od permutacije broja 0 - (1,2,3,4,5) do permutacije broja 119 - (5,4,3,2,1)), nađimo 101. permutaciju: 100 = 4!* 4 + 3!*0 + 2!*2 + 1!*0 = 96 + 4; neka je ti koeficijent za broj i!, tada je t4 = 4, t3 = 0, t2 = 2, t1 = 0, tada: broj elemenata manji od 5, ali smještenih desno je 4; broj elemenata manji od 4, ali smještenih desno je 0; broj elemenata manji od 3, ali s desne strane je 2; broj elemenata manji od 2, ali smještenih desno je 0 (posljednji element u permutaciji se “stavlja” na jedino preostalo mjesto) - dakle, 101. permutacija će izgledati ovako: (5,3,1,2 ,4) Provjera ove metode može se provesti izravnim brojanjem inverzija za svaki element permutacije.
Fibonaccijev sustav brojeva na temelju Fibonaccijevih brojeva. Svaki prirodni broj je predstavljen u obliku:
, gdje su Fibonaccijevi brojevi, a koeficijenti imaju konačan broj jedinica i ne postoje dvije jedinice u nizu.Nepozicijski brojevni sustavi
U nepozicijskim brojevnim sustavima vrijednost koju znamenka označava ne ovisi o njezinu položaju u broju. U tom slučaju sustav može nametnuti ograničenja na položaj brojeva, na primjer, tako da su raspoređeni silaznim redoslijedom.
Binomni brojevni sustav
Predstavljanje pomoću binomnih koeficijenata
, Gdje .Sustav preostalih klasa (RSS)
Predstavljanje broja u sustavu klasa ostataka temelji se na konceptu ostatka i kineskom teoremu o ostatku. RNS je određen skupom relativno prostih moduli s umnoškom na način da je svaki cijeli broj iz segmenta pridružen skupu ostataka, gdje
…Istodobno, kineski teorem o ostatku jamči jedinstvenost prikaza za brojeve iz intervala.
U RNS-u, aritmetičke operacije (zbrajanje, oduzimanje, množenje, dijeljenje) izvode se po komponentama ako se zna da je rezultat cijeli broj i također leži u .
Nedostaci RNS-a su mogućnost predstavljanja samo ograničenog broja brojeva, kao i nedostatak učinkovitih algoritama za usporedbu brojeva predstavljenih u RNS-u. Usporedba se obično provodi prevođenjem argumenata iz RNS-a u mješoviti sustav brojeva radix.
Stern–Brocotov brojevni sustav- način zapisivanja pozitivnih racionalnih brojeva, temeljen na Stern–Brocotovom stablu.
Brojevni sustavi različitih naroda
Brojevni sustav jedinica
Očigledno, kronološki prvi brojevni sustav svakog naroda koji je ovladao brojanjem. Prirodni broj prikazuje se ponavljanjem istog znaka (crtica ili točka). Na primjer, da biste prikazali broj 26, morate nacrtati 26 linija (ili napraviti 26 zareza na kosti, kamenu itd.). Nakon toga, radi lakšeg uočavanja velikih brojeva, ti su znakovi grupirani u skupine od tri ili pet. Tada se jednake grupe znakova počinju zamjenjivati nekim novim znakom - tako nastaju prototipovi budućih brojeva.
Staroegipatski brojevni sustav
Babilonski brojevni sustav
Abecedni brojevni sustavi
Abecedne brojevne sustave koristili su stari Armenci, Gruzijci, Grci (jonski brojevni sustav), Arapi (abjadia), Židovi (vidi gematrija) i drugi narodi Bliskog istoka. U slavenskim liturgijskim knjigama grčki alfabetski sustav preveden je na ćirilicu.
Židovski brojevni sustav
Grčki brojevni sustav
Rimski brojevni sustav
Kanonski primjer gotovo nepozicijskog brojevnog sustava je rimski, koji kao brojeve koristi latinična slova:
Zalažem se za 1,
V - 5,
X - 10,
L - 50,
C - 100,
D - 500,
M - 1000
Na primjer, II = 1 + 1 = 2
ovdje simbol I označava 1 bez obzira na mjesto u broju.
Zapravo, rimski sustav nije potpuno nepozicioniran, jer se od njega oduzima manja znamenka koja dolazi prije veće, na primjer:
IV = 4, dok je:
VI = 6
Mayanski brojevni sustav
vidi također
Bilješke
Linkovi
- Gaškov S. B. Brojevni sustavi i njihove primjene. - M.: MTsNMO, 2004. - (Biblioteka “Matematičko obrazovanje”).
- Fomin S.V. Sustavi brojeva. - M.: Nauka, 1987. - 48 str. - (Popularna predavanja iz matematike).
- Yaglom I. Sustavi brojeva // Kvantni. - 1970. - br. 6. - str. 2-10.
- Brojevi i brojevni sustavi. Internetska enciklopedija oko svijeta.
- Stakhov A. Uloga brojevnih sustava u povijesti računala.
- Mikushin A.V. Sustavi brojeva. Tečaj predavanja "Digitalni uređaji i mikroprocesori"
- Butler J. T., Sasao T. Redundantni brojčani sustavi s više vrijednosti U članku se govori o brojevnim sustavima koji koriste znamenke veće od jedan i dopuštaju redundanciju u predstavljanju brojeva
Zaklada Wikimedia. 2010.
volovi (kategorije). Ovaj se pristup koristi u prijenosu, pohrani i obradi informacija i obično nije povezan sa semantičkim sadržajem informacija.
1.5.2. Probabilistički pristup
U Teorija informacija, informacija se definira kao uklonjena nesigurnost. Ovo uzima u obzir vrijednost informacije za primatelja. Količina informacija određena je time koliko se mjera nesigurnosti (entropija) smanjuje nakon primitka poruke ili pojave događaja.
Jedinicom količine informacije (bit) smatra se količina informacije koja sadrži poruku koja smanjuje informacijsku nesigurnost za 2 puta. Općenito, količina informacija (H) sadržana u poruci da se dogodio jedan od N jednako vjerojatnih događaja određuje se na sljedeći način:
Skupina od 8 bitova naziva se bajt. Ako je bit minimalna jedinica informacije, onda je bajt glavna. Postoje izvedene jedinice informacija:
1 bajt = 8 bita;
1 kilobajt = 210 bajtova = 1024 bajta;
1 megabajt = 220 bajtova = 1024 kilobajta;
1 gigabajt = 230 bajtova = 1024 megabajta;
1 terabajt = 240 bajtova = 1024 gigabajta.
1.6. Brojevni sustavi koji se koriste u informatici
Brojevni sustav je skup tehnika i pravila za pisanje brojeva pomoću znamenki. Postoje nepozicijski i pozicijski sustavi brojeva.
U U nepozicijskom brojevnom sustavu svaki simbol ima svoje specifično značenje, koje ne ovisi o položaju simbola u zapisu broja. Na primjer, u rimskom brojevnom sustavu
I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000. Broj 77 napisan je LXXVII.
U U pozicijskom brojevnom sustavu vrijednost bilo koje znamenke na slici broja ovisi o njezinu položaju (položaju) u nizu znamenki koje predstavljaju dati broj. Na primjer: 77 - 7 jedinica i 7 desetica.
Svaki položajni brojevni sustav ima strogo definiran broj simbola (znamenki) za predstavljanje bilo kojeg broja:
– binarni - 2: 0 i 1;
– decimalno - 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Broj znamenki koje se koriste u pozicijskom brojevnom sustavu za zapis brojeva naziva se baza brojevnog sustava. Osnova brojevnog sustava može biti bilo koji prirodni broj.
Neka je q baza sustava, tada se bilo koji broj u brojevnom sustavu s bazom q može prikazati kao:
A q = a n q n + a n –1 q n –1 + ... + a 1 q 1 + a 0 q 0 + a –1 q –1 + a –2 q –2 + ... + a –k q–k , (3) gdje je A q broj zapisan u brojevnom sustavu s bazom q,
n + 1 - broj znamenki cijelog dijela broja,
i i su znamenke broja, s 0 ≤ a i< q ,
k - broj znamenki u razlomačkom dijelu broja.
U informatici se koriste samo položajni brojevni sustavi: decimalni, binarni, oktalni, heksadecimalni.
1.6.1. Pravila za pretvaranje brojeva iz jednog brojevnog sustava u drugi
Pravilo 1. Za pretvaranje cijelog decimalnog broja A u brojevni sustav s bazom q potrebno je broj A dijeliti s bazom q dok se ne dobije cijeli ostatak manji od q. Dobiveni kvocijent treba ponovno podijeliti s q dok se ne dobije cijeli ostatak manji od q, itd. dok zadnji kvocijent ne bude manji od q. Tada decimalni broj A u brojevnom sustavu s bazom q treba napisati kao niz ostataka dijeljenja obrnutim redoslijedom od njihova primitka, pri čemu najviša znamenka daje posljednji kvocijent.
Pravilo 2. Da biste decimalni razlomak pretvorili u brojevni sustav s bazom q, pomnožite taj broj s bazom q. Cjelobrojni dio umnoška bit će prva znamenka broja u brojevnom sustavu s bazom q. Zatim, odbacivanje cijelog dijela, ponovno množenje s bazom q, itd. dok se ne dobije potreban broj znamenki u novom brojevnom sustavu ili dok se ne završi prevođenje.
Pravilo 3. Mješoviti brojevi decimalnog brojevnog sustava prevode se u dva koraka: posebno cjelobrojni dio po svom pravilu, a posebno razlomljeni dio po svom pravilu. Zatim se zapisuje ukupni rezultat, čiji se razlomački dio odvaja zarezom.
Pravilo 4. Za prevođenje broja iz brojevnog sustava s bazom q u decimalni brojevni sustav treba koristiti oblik zapisivanja broja u obliku (3).
Pravilo 5. Za pretvorbu cijelog broja iz binarnog brojevnog sustava u oktalni sustav potreban vam je niz binarnih znamenki različitih veličina.




 Primjer odgođenih poreznih obveza Odgođene porezne obveze obračunavaju se kao dio
Primjer odgođenih poreznih obveza Odgođene porezne obveze obračunavaju se kao dio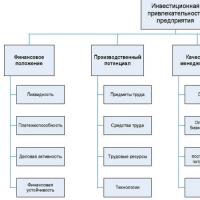 Kako povećati investicijsku atraktivnost organizacije Mjere za povećanje investicijske atraktivnosti poduzeća
Kako povećati investicijsku atraktivnost organizacije Mjere za povećanje investicijske atraktivnosti poduzeća Zašto sanjate svoju trudnoću?
Zašto sanjate svoju trudnoću? Test poslovne sposobnosti
Test poslovne sposobnosti „Knjiga iz snova Štakor je sanjao zašto Štakor sanja u snu
„Knjiga iz snova Štakor je sanjao zašto Štakor sanja u snu Gdje je umro Napoleon Bonaparte?
Gdje je umro Napoleon Bonaparte?