Λόγοι για την εμφάνιση ξένων ριζών κατά την επίλυση εξισώσεων. Εργαστήριο «Επίλυση τριγωνομετρικών εξισώσεων». Ισοδύναμοι μετασχηματισμοί εξισώσεων
Το θέμα των τριγωνομετρικών εξισώσεων ξεκινά με μια σχολική διάλεξη, η οποία δομείται με τη μορφή ευρετικής συνομιλίας. Η διάλεξη συζητά θεωρητικό υλικό και παραδείγματα επίλυσης όλων των τυπικών προβλημάτων σύμφωνα με το σχέδιο:
- Οι απλούστερες τριγωνομετρικές εξισώσεις.
- Βασικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.
- Ομογενείς εξισώσεις.
Στα επόμενα μαθήματα ξεκινά η ανεξάρτητη ανάπτυξη δεξιοτήτων, με βάση την εφαρμογή της αρχής της κοινής δραστηριότητας δασκάλου και μαθητή. Πρώτον, τίθενται στόχοι για τους μαθητές, δηλ. καθορίζεται ποιος θέλει να μάθει τίποτα περισσότερο από αυτό που απαιτείται από το κρατικό πρότυπο και ποιος είναι έτοιμος να κάνει περισσότερα.
Η τελική διάγνωση δημιουργείται λαμβάνοντας υπόψη τη διαφοροποίηση του επιπέδου, η οποία επιτρέπει στους μαθητές να προσδιορίσουν συνειδητά τις ελάχιστες γνώσεις που είναι απαραίτητες για τη λήψη του βαθμού «3». Με βάση αυτό, επιλέγονται πολυεπίπεδα υλικά για τη διάγνωση των γνώσεων των μαθητών. Αυτή η εργασία επιτρέπει μια ατομική προσέγγιση των μαθητών, συμπεριλαμβανομένων όλων σε δραστηριότητες συνειδητής μάθησης, αναπτύσσοντας δεξιότητες αυτοοργάνωσης και αυτομάθησης και διασφαλίζοντας τη μετάβαση στην ενεργό, ανεξάρτητη σκέψη.
Το σεμινάριο διεξάγεται μετά την εξάσκηση των βασικών δεξιοτήτων επίλυσης τριγωνομετρικών εξισώσεων. Αρκετά μαθήματα πριν το σεμινάριο δίνονται στους μαθητές ερωτήσεις που θα συζητηθούν κατά τη διάρκεια του σεμιναρίου.
Το σεμινάριο αποτελείται από τρία μέρη.
1. Το εισαγωγικό μέρος καλύπτει όλο το θεωρητικό υλικό, συμπεριλαμβανομένης μιας εισαγωγής στα προβλήματα που θα προκύψουν κατά την επίλυση μιγαδικών εξισώσεων.
2. Στο δεύτερο μέρος εξετάζεται η λύση των εξισώσεων της μορφής:
- και cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- εξισώσεις επιλύσιμες με μείωση του βαθμού.
Αυτές οι εξισώσεις χρησιμοποιούν καθολική υποκατάσταση, τύπους μείωσης βαθμών και τη μέθοδο βοηθητικού ορίσματος.
3. Στο τρίτο μέρος συζητούνται τα προβλήματα της απώλειας ριζών και η απόκτηση ξένων ριζών. Δείχνει πώς να επιλέξετε ρίζες.
Οι μαθητές εργάζονται σε ομάδες. Για να λυθούν τα παραδείγματα, καλούνται καλά εκπαιδευμένοι τύποι που μπορούν να δείξουν και να εξηγήσουν το υλικό.
Το σεμινάριο απευθύνεται σε έναν καλά προετοιμασμένο μαθητή, γιατί... αντιμετωπίζει ζητήματα κάπως πέρα από το πεδίο του υλικού του προγράμματος. Περιλαμβάνει εξισώσεις πιο σύνθετης μορφής και ειδικότερα αντιμετωπίζει προβλήματα που αντιμετωπίζονται κατά την επίλυση μιγαδικών τριγωνομετρικών εξισώσεων.
Το σεμινάριο πραγματοποιήθηκε για μαθητές των τάξεων 10-11. Κάθε μαθητής είχε την ευκαιρία να διευρύνει και να εμβαθύνει τις γνώσεις του σε αυτό το θέμα, να συγκρίνει το επίπεδο των γνώσεών του όχι μόνο με τις απαιτήσεις για έναν απόφοιτο σχολείου, αλλά και με τις απαιτήσεις για όσους εισέρχονται στο V.U.Z.
ΣΕΜΙΝΑΡΙΟ
Θέμα:"Επίλυση Τριγωνομετρικών Εξισώσεων"
Στόχοι:
- Γενίκευση γνώσεων για την επίλυση τριγωνομετρικών εξισώσεων όλων των τύπων.
- Εστίαση σε προβλήματα: απώλεια ριζών. ξένες ρίζες? επιλογή ρίζας.
ΚΑΤΑ ΤΑ ΜΑΘΗΜΑΤΑ.
I. Εισαγωγικό μέρος
1. Βασικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων
- Παραγοντοποίηση.
- Εισαγωγή νέας μεταβλητής.
- Λειτουργική γραφική μέθοδος.
2. Μερικοί τύποι τριγωνομετρικών εξισώσεων.
- Εξισώσεις που ανάγονται σε δευτεροβάθμιες εξισώσεις σε σχέση με cos x = t, sin x = t.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Bsinx + C = 0.
Επιλύονται με την εισαγωγή μιας νέας μεταβλητής.
- Ομογενείς εξισώσεις πρώτου και δεύτερου βαθμού
Εξίσωση πρώτου βαθμού: Asinx + Bcosx = 0 διαιρούμε με cos x, παίρνουμε Atg x + B = 0
Εξίσωση δεύτερου βαθμού: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 διαίρεση με cos 2 x, παίρνουμε Atg 2 x + Btgx + C = 0
Επιλύονται με παραγοντοποίηση και με την εισαγωγή μιας νέας μεταβλητής.
Ισχύουν όλες οι μέθοδοι.
- Κατηφορικός:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Επιλύεται με τη μέθοδο παραγοντοποίησης.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Εξίσωση της μορφής: A(sinx + cosx) + Bsin2x + C = 0.
Ανάγεται σε τετράγωνο σε σχέση με t = sinx + cosx; sin2x = t 2 – 1.
3. Φόρμουλες.
x + 2 n; Απαιτείται έλεγχος!
- Μειούμενη ισχύς: cos 2 x = (1 + cos2x): 2; αμαρτία 2 x = (1 – cos 2x): 2
- Μέθοδος βοηθητικού ορίσματος.
Ας αντικαταστήσουμε το Acosx + Bsinx με το Csin (x + ), όπου sin = a/C. cos=v/c;
– βοηθητικό επιχείρημα.
4. Κανόνες.
- Αν δείτε τετράγωνο, χαμηλώστε τη μοίρα.
- Αν δείτε ένα κομμάτι, κάντε ένα άθροισμα.
- Αν δείτε το ποσό, κάντε τη δουλειά.
5. Απώλεια ριζών, επιπλέον ρίζες.
- Απώλεια ριζών: διαιρέστε με g(x); επικίνδυνες φόρμουλες (καθολική υποκατάσταση). Με αυτές τις πράξεις περιορίζουμε το πεδίο ορισμού.
- Υπερβολικές ρίζες: ανυψώνονται σε ομοιόμορφη ισχύ. πολλαπλασιάστε με g(x) (απαλλαγείτε από τον παρονομαστή). Με αυτές τις λειτουργίες διευρύνουμε το πεδίο ορισμού.
II. Παραδείγματα τριγωνομετρικών εξισώσεων
1. Εξισώσεις της μορφής Asinx + Bcosx = C
1) Καθολική αντικατάσταση.Ο.Δ.Ζ. x – οποιοδήποτε.
3 αμαρτία 2x + cos 2x + 1 = 0.
tgx = u. x/2 + n;
![]() u = – 1/3.
u = – 1/3.
tan x = –1/3, x = αρκτάν (–1/3) + k, k Z.
Εξέταση: 3sin( + 2n) + cos( + 2n) + 1= 3 sin + cos + 1 = 0 – 1 + 1 = 0.
x = /2 + n, n e Z. Είναι η ρίζα της εξίσωσης.
Απάντηση: x = αρκτάνη(–1/3) + k, k Z. x = /2 + n, n Z.
2) Λειτουργική γραφική μέθοδος. Ο Ο.Δ.Ζ. x – οποιοδήποτε.
Sinx – cosx = 1
Sinx = cosx + 1.
Ας σχεδιάσουμε τις συναρτήσεις: y = sinx, y = cosx + 1.

Απάντηση: x = /2 + 2 n, Z; x = + 2k, k Z.
3) Εισαγωγή βοηθητικού ορίσματος. O.D.Z.: x – οποιαδήποτε.
8cosx + 15 sinx = 17.
![]()
8/17 cosx + 15/17 sinx = 1, επειδή (8/17) 2 + (15/17) 2 = 1, τότε υπάρχει τέτοια που αμαρτία = 8/17,
cos = 15/17, που σημαίνει αμαρτία cosx + sinx cos = 1; = arcsin 8/17.
Απάντηση: x = /2 + 2n – , x = /2 + 2n – arcsin 8/17, n Z.
2. Μείωση της σειράς: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). αμαρτία 2 3x + αμαρτία 2 4x + αμαρτία 2 6x + αμαρτία 2 7x = 2. Ο.Δ.Ζ.: x – οποιαδήποτε.
1 – cos 6x + 1 – cos 8x + 1 – cos 12x + 1 – cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x(cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Απάντηση: x = /20 + n/10, n Z. x = /6 + k/3, k Z, x = /2 + m, m Z.
| Στο | k = 1 και m = 0 k = 4 και m = 1. |
η σειρά είναι ίδια. |
3. Αναγωγή στην ομοιογένεια. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 3 sinx cosx + 6 cos 2 x = 5. ODZ: x – οποιαδήποτε.
5 sin 2 x + 3 sinx cosx + 6cos 2 x – 5 sin 2 x – 5 cos 2 x = 0
3 sinxcosx + cos 2 x = 0 (1) δεν μπορεί να διαιρεθεί με cos 2 x, αφού χάνουμε ρίζες.
cos 2 x = 0 ικανοποιεί την εξίσωση.
cosx (3 sinx + cosx) = 0
cosx = 0. 3 sinx + cosx = 0.
x = /2 + k, k Z. tgx = –1/3, x = –/6 + n, n Z.
Απάντηση: x = /2 + k, k Z. , x = –/6 + n, n Z
4. Εξίσωση της μορφής: A(sinx + cosx) + B sin2x + C = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. O.D.Z.: x – οποιαδήποτε.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | <
2
2 t 2 – 5t + 2 = 0. t 1 = 2, t 2 = S.
sinx + cosx = S. cosx = sin(x + /2),
sinx +sin(x + /2) = 1/2,
2sin(x + /4) cos(–/4) = 1/2
sin(x + /4) = 1/22;
x +/4 = (–1) k arcsin(1/2 O 2) + k, k Z.
Απάντηση: x = (–1) k arcsin(1/22) – /4 + k, k Z.
5. Παραγοντοποίηση.
1) cos 2 x – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2)(cosx + 2 sinx) = 0.
1) cosx = 2, χωρίς ρίζες.
2) cosx + 2 sinx = 0
2tgx + 1 = 0
Απάντηση: x = αρκτάνη(1/2) + n, n Z.
III. Προβλήματα που προκύπτουν κατά την επίλυση τριγωνομετρικών εξισώσεων
1. Απώλεια ριζών: διαιρέστε με g(x); Χρησιμοποιούμε επικίνδυνες φόρμουλες.
1) Βρείτε το σφάλμα.
1 – cosx = sinx *sinx/2,
1 – cosx = 2sin 2 x/2 τύπος.
2 αμαρτία 2 x/2 = 2 sinx/2* сosx/2* sinx/2 διαίρεση με 2 αμαρτία 2 x/2,
1 = cosx/2
x/2 = 2n, x = 4n, n" Z.
Χαμένες ρίζες sinx/2 = 0, x = 2k, k Z.
Σωστή λύση: 2sin 2 x/2(1 – cosx/2) = 0.
| αμαρτία 2 x/2 = 0 x = 2k, k Z. |
1 – cosx /2 = 0 x = 4p n, n Z. |
2. Εξωτερικές ρίζες: απαλλαγούμε από τον παρονομαστή. αυξήσει σε ομοιόμορφη ισχύ.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 3) = 0. O.D.Z.: sin2x 3 / 2.
2cos3x sinx – cos3x + 2sinx – 1 = 0
(cos3x + 1)(2sinx – 1) = 0
| 1). сos3x + 1 = 0 x = /3 + 2n/3, n Z. |
2). 2sinx – 1 = 0 x = (–1) k /6 + k, k Z. |

| Ι. x = /3 + 2n/3 1. n = 0 αμαρτία 2/3 = 3/2 δεν ικανοποιούν. Ο Ο.Δ.Ζ. 2. n = 1 3. n = 2 |
II. x = (–1) k /6 + k, k Z 1.k = 0 αμαρτία 2/6 = 3/2 δεν ικανοποιούν τον Ο.Δ.Ζ. 2. k = 1 αμαρτία 2*5/6 = –3 / 2 ικανοποιεί την Ο.Δ.Ζ. |
Απάντηση: x = + 2k, x = 5/3 + 2k, x = 5/6 + 2k, k Z. t = 5 sin3x = 0
§ 1. ΧΑΜΕΝΕΣ ΚΑΙ ΞΕΧΑΣΜΕΝΕΣ ΡΙΖΕΣ ΚΑΤΑ ΤΗΝ ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΕΩΝ (ΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ)
ΥΛΙΚΟ ΑΝΑΦΟΡΑΣ
1. Δύο θεωρήματα στην § 3 του Κεφαλαίου VII μίλησαν για το ποιες ενέργειες σε εξισώσεις δεν παραβιάζουν την ισοδυναμία τους.
2. Ας εξετάσουμε τώρα πράξεις σε εξισώσεις που μπορούν να οδηγήσουν σε μια νέα εξίσωση που είναι άνιση με την αρχική εξίσωση. Αντί για γενικούς προβληματισμούς, θα περιοριστούμε στην εξέταση μόνο συγκεκριμένων παραδειγμάτων.
3. Παράδειγμα 1. Ας ανοίξουμε τις αγκύλες αυτής της εξίσωσης, μεταφέρουμε όλους τους όρους στην αριστερή πλευρά και λύνουμε την δευτεροβάθμια εξίσωση. Οι ρίζες του είναι
Εάν μειώσετε και τις δύο πλευρές της εξίσωσης με έναν κοινό παράγοντα, θα λάβετε μια εξίσωση που είναι άνιση με την αρχική, αφού έχει μόνο μία ρίζα
Έτσι, η μείωση και των δύο πλευρών της εξίσωσης με έναν παράγοντα που περιέχει το άγνωστο μπορεί να έχει ως αποτέλεσμα να χαθούν οι ρίζες της εξίσωσης.
4. Παράδειγμα 2. Δεδομένου ότι η εξίσωση αυτή έχει μία μόνο ρίζα, και λαμβάνουμε την επίλυση αυτής της εξίσωσης.
Βλέπουμε ότι η νέα εξίσωση δεν είναι ισοδύναμη με την αρχική εξίσωση Η ρίζα είναι η ρίζα της εξίσωσης που, αφού τετραγωνιστούν και οι δύο πλευρές, οδηγεί στην εξίσωση
5. Οι ξένες ρίζες μπορούν επίσης να εμφανιστούν όταν και οι δύο πλευρές της εξίσωσης πολλαπλασιάζονται με έναν παράγοντα που περιέχει ένα άγνωστο, εάν αυτός ο παράγοντας εξαφανιστεί για πραγματικές τιμές του x.
Παράδειγμα 3. Αν πολλαπλασιάσουμε και τις δύο πλευρές της εξίσωσης με τότε παίρνουμε μια νέα εξίσωση η οποία, αφού μεταφέρει τον όρο από τη δεξιά πλευρά στην αριστερή και τον συντελεστή σε παράγοντες, δίνει μια εξίσωση από οποιαδήποτε
Η ρίζα δεν ικανοποιεί μια εξίσωση που έχει μόνο μία ρίζα
Από εδώ συμπεραίνουμε: όταν τετραγωνίζουμε και τις δύο πλευρές της εξίσωσης (γενικά σε άρτια ισχύ), καθώς και όταν πολλαπλασιάζουμε με έναν παράγοντα που περιέχει ένα άγνωστο και εξαφανίζεται σε πραγματικές τιμές του αγνώστου, μπορεί να εμφανιστούν εξωτερικές ρίζες.
Όλες οι σκέψεις που εκφράζονται εδώ σχετικά με το ζήτημα της απώλειας και εμφάνισης εξωτερικών ριζών μιας εξίσωσης ισχύουν εξίσου για οποιεσδήποτε εξισώσεις (αλγεβρικές, τριγωνομετρικές, κ.λπ.).
6. Μια εξίσωση λέγεται αλγεβρική αν εκτελούνται μόνο αλγεβρικές πράξεις στο άγνωστο - πρόσθεση, αφαίρεση, πολλαπλασιασμός, διαίρεση, εκθέτοντας και εξαγωγή ρίζας με φυσικό εκθέτη (και ο αριθμός αυτών των πράξεων είναι πεπερασμένος).
Έτσι, για παράδειγμα, οι εξισώσεις

είναι αλγεβρικές, και οι εξισώσεις

ΔΟΝΤΙΑ. Τα δόντια των σπονδυλωτών είναι εντελώς παρόμοια σε δομή και ανάπτυξη με τα πλακοειδή λέπια που καλύπτουν ολόκληρο το δέρμα των ψαριών καρχαρία. Δεδομένου ότι ολόκληρη η στοματική κοιλότητα, και εν μέρει η φαρυγγική κοιλότητα, είναι επενδεδυμένη με εξωδερμικό επιθήλιο, ένα τυπικό πλακοειδές... ...
ΠΝΕΥΜΟΝΙΚΗ ΦΥΜΑΤΙΩΣΗ- ΠΝΕΥΜΟΝΙΚΗ ΦΥΜΑΤΙΩΣΗ. Περιεχόμενα: I. Παθολογική ανατομία...........110 II. Ταξινόμηση της πνευμονικής φυματίωσης.... 124 III. Κλινική..........................128 IV. Διαγνωστικά..........................160 V. Πρόγνωση................. .......... 190 VI. Θεραπεία … Μεγάλη Ιατρική Εγκυκλοπαίδεια
ΔΗΛΗΤΗΡΙΑΣΗ- ΔΗΛΗΤΗΡΙΑΣΗ. Δηλητηρίαση σημαίνει «διαταραχές στις λειτουργίες των ζώων». οργανισμοί, που προκαλούνται από εξωγενείς ή ενδογενείς, χημικά ή φυσικά και χημικά δραστικές ουσίες, οι οποίες είναι ξένες ως προς την ποιότητα, την ποσότητα ή τη συγκέντρωση... ... Μεγάλη Ιατρική Εγκυκλοπαίδεια
Βακτήρια όζων ψυχανθών- Παλαιοντολογικά δεδομένα δείχνουν ότι τα αρχαιότερα όσπρια που είχαν οζίδια ήταν κάποια φυτά που ανήκαν στην ομάδα των Eucaesalpinioideae. Στα σύγχρονα είδη ψυχανθών, έχουν βρεθεί οζίδια... Βιολογική εγκυκλοπαίδεια
Λίστα επεισοδίων της σειράς κινουμένων σχεδίων "Luntik"- Αυτό το άρθρο δεν διαθέτει συνδέσμους προς πηγές πληροφοριών. Οι πληροφορίες πρέπει να είναι επαληθεύσιμες, διαφορετικά ενδέχεται να τεθούν υπό αμφισβήτηση και να διαγραφούν. Μπορείτε να... Wikipedia
ΦΥΤΟ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝ- Η ζωή ενός φυτού, όπως και κάθε άλλου ζωντανού οργανισμού, είναι ένα σύνθετο σύνολο αλληλένδετων διαδικασιών. Το πιο σημαντικό από αυτά, όπως είναι γνωστό, είναι η ανταλλαγή ουσιών με το περιβάλλον. Το περιβάλλον είναι η πηγή από την οποία... ... Βιολογική εγκυκλοπαίδεια
Λίστα επεισοδίων της σειράς "Luntik"- Κύριο άρθρο: Οι περιπέτειες του Λούντικ και των φίλων του Περιεχόμενα 1 Αριθμός επεισοδίων 2 Λίστα επεισοδίων της σειράς κινουμένων σχεδίων Ο Λούντικ και οι φίλοι του ... Wikipedia
Ασθένειες των οπωροφόρων δέντρων- Τα οπωροφόρα δέντρα, χάρη στη συνεχή ανθρώπινη φροντίδα γι' αυτά, θα πρέπει να φτάσουν σε πολύ μεγαλύτερη ηλικία από τους ακαλλιέργητους συγγενείς τους, αν όχι για τις αντισταθμιστικές επιρροές πολλών συνθηκών του ίδιου του πολιτισμού, δηλαδή των απαιτήσεων που θέτουμε... ...
Δασική υλοτόμηση- Η συγκομιδή των δασών ή η εξόρυξη δασικού εισοδήματος με τη μορφή ξύλου και φλοιού, μπορεί να γίνει με δύο τρόπους: σκάβοντας ή ξεριζώνοντας ολόκληρα δέντρα, δηλαδή κορμούς μαζί με τις ρίζες, ή χωριστά, τμηματικά, πρώτα κομμένα ή αφαιρούμενα από... ... Εγκυκλοπαιδικό Λεξικό F.A. Brockhaus και I.A. Έφρων
Grosh- (Πολωνικά grosz, από τα γερμανικά Groschen, από τα λατινικά grossus (dēnārius) «χοντρό denarius») νόμισμα διαφόρων χωρών και εποχών. Περιεχόμενα 1 Η εμφάνιση μιας δεκάρας ... Wikipedia
νομίσματα των ΗΠΑ- 20 δολάρια Saint Gaudens το πιο όμορφο και ακριβό νόμισμα των ΗΠΑ Τα νομίσματα των ΗΠΑ είναι νομίσματα που κόβονται στο νομισματοκοπείο των ΗΠΑ. Παράγεται από το 1792... Wikipedia
Βιβλία
- Οι κύριες αιτίες της τριχόπτωσης στις γυναίκες, Alexey Michman, Έξι στις δέκα γυναίκες υποφέρουν από τριχόπτωση κάποια στιγμή στη ζωή τους. Η τριχόπτωση μπορεί να συμβεί για διάφορους λόγους, όπως κληρονομικότητα, ορμονικές αλλαγές σε... Κατηγορία:
Στο τελευταίο μάθημα χρησιμοποιήσαμε τρία βήματα για να λύσουμε εξισώσεις.
Το πρώτο στάδιο είναι τεχνικό. Χρησιμοποιώντας μια αλυσίδα μετασχηματισμών από την αρχική εξίσωση, φτάνουμε σε μια αρκετά απλή, την οποία λύνουμε και βρίσκουμε τις ρίζες.
Το δεύτερο στάδιο είναι η ανάλυση λύσης. Αναλύουμε τους μετασχηματισμούς που πραγματοποιήσαμε και διαπιστώνουμε αν είναι ισοδύναμοι.
Το τρίτο στάδιο είναι η επαλήθευση. Ο έλεγχος όλων των ριζών που βρέθηκαν αντικαθιστώντας τες στην αρχική εξίσωση είναι υποχρεωτικός όταν εκτελούνται μετασχηματισμοί που μπορούν να οδηγήσουν σε μια συνεπακόλουθη εξίσωση
Είναι πάντα απαραίτητο να διακρίνουμε τρία στάδια κατά την επίλυση μιας εξίσωσης;
Φυσικά και όχι. Όπως, για παράδειγμα, στην επίλυση αυτής της εξίσωσης. Στην καθημερινότητα συνήθως δεν διακρίνονται. Αλλά όλα αυτά τα στάδια πρέπει να "κρατηθούν υπόψη" και να πραγματοποιηθούν με τη μια ή την άλλη μορφή. Είναι επιτακτική ανάγκη να αναλυθεί η ισοδυναμία των μετασχηματισμών. Και αν η ανάλυση δείξει ότι πρέπει να γίνει έλεγχος, τότε είναι υποχρεωτικός. Διαφορετικά, η εξίσωση δεν μπορεί να θεωρηθεί λυμένη σωστά.
Είναι πάντα δυνατός ο έλεγχος των ριζών μιας εξίσωσης μόνο με αντικατάσταση;
Εάν χρησιμοποιήθηκαν ισοδύναμοι μετασχηματισμοί κατά την επίλυση της εξίσωσης, τότε δεν απαιτείται επαλήθευση. Κατά τον έλεγχο των ριζών μιας εξίσωσης, το ODZ (επιτρεπόμενο εύρος τιμών) χρησιμοποιείται πολύ συχνά Εάν είναι δύσκολο να ελεγχθεί χρησιμοποιώντας το ODZ, τότε πραγματοποιείται αντικαθιστώντας το στην αρχική εξίσωση.
Ασκηση 1
Λύστε την εξίσωση τετραγωνική ρίζα δύο x συν τρία ισούται με ένα συν x.
Λύση
Το ODZ της εξίσωσης καθορίζεται από ένα σύστημα δύο ανισώσεων: δύο x συν τρία είναι μεγαλύτερο ή ίσο με μηδέν και ένα συν x είναι μεγαλύτερο ή ίσο με μηδέν. Η λύση είναι x μεγαλύτερη ή ίση με μείον ένα.
Ας τετραγωνίσουμε και τις δύο πλευρές της εξίσωσης, μεταφέρουμε τους όρους από τη μια πλευρά της εξίσωσης στην άλλη, προσθέτουμε παρόμοιους όρους και λαμβάνουμε μια τετραγωνική εξίσωση x στο τετράγωνο ίσον δύο. Οι ρίζες του είναι
x πρώτο, δεύτερο ίσον συν ή πλην την τετραγωνική ρίζα του δύο.
Εξέταση
Η τιμή του x πρώτα είναι ίση με την τετραγωνική ρίζα του δύο είναι η ρίζα της εξίσωσης, αφού περιλαμβάνεται στο ODZ.
Η τιμή του x δευτερολέπτου είναι ίση με μείον την τετραγωνική ρίζα του δύο δεν είναι η ρίζα της εξίσωσης, γιατί δεν περιλαμβάνεται στο ΔΖ.
Ας ελέγξουμε ότι η ρίζα x είναι ίση με την τετραγωνική ρίζα δύο, αντικαθιστώντας την στην αρχική ισότητα, παίρνουμε
η ισότητα είναι αληθής, που σημαίνει ότι το x ισούται με την τετραγωνική ρίζα του δύο είναι η ρίζα της εξίσωσης.
Απάντηση: τετραγωνική ρίζα δύο.
Εργασία 2
Λύστε την εξίσωση τετραγωνική ρίζα του x μείον οκτώ ισούται με πέντε μείον x.
Λύση
Το ODZ μιας ανορθολογικής εξίσωσης προσδιορίζεται από ένα σύστημα δύο ανισώσεων: το x μείον οκτώ είναι μεγαλύτερο ή ίσο με μηδέν και πέντε μείον το x είναι μεγαλύτερο ή ίσο με μηδέν. Λύνοντάς το, διαπιστώνουμε ότι αυτό το σύστημα δεν έχει λύσεις. Η ρίζα της εξίσωσης δεν μπορεί να είναι καμία από τις τιμές της μεταβλητής x.
Απάντηση: χωρίς ρίζες.
Εργασία 3
Λύστε την εξίσωση τετραγωνική ρίζα του x σε κύβους συν τέσσερα x μείον ένα μείον οκτώ τετραγωνικές ρίζες του x στην τέταρτη δύναμη μείον x ισούται με τετραγωνική ρίζα του x σε κύβους μείον ένα συν δύο τετραγωνικές ρίζες του x.
Λύση
Η εύρεση του ODZ σε αυτή την εξίσωση είναι αρκετά δύσκολη.
Ας πραγματοποιήσουμε τον μετασχηματισμό: τετραγωνίστε και τις δύο πλευρές αυτής της εξίσωσης,
Ας μετακινήσουμε όλους τους όρους στην αριστερή πλευρά της εξίσωσης και φέρουμε όμοιους όρους, γράψουμε δύο ρίζες κάτω από έναν, πάρουμε παρόμοιες ρίζες, φέρουμε όμοιες, διαιρούμε με τον συντελεστή μείον 12 και συνυπολογίζουμε τη ριζική έκφραση, παίρνουμε μια εξίσωση στο μορφή προϊόντος δύο παραγόντων ίσων με μηδέν. Αφού το λύσαμε, βρίσκουμε τις ρίζες:
Το x πρώτο είναι ίσο με ένα, το x δεύτερο είναι ίσο με μηδέν.
Δεδομένου ότι αυξήσαμε και τις δύο πλευρές της εξίσωσης σε άρτια ισχύ, ο έλεγχος των ριζών είναι υποχρεωτικός.
Εξέταση
Αν το x είναι ίσο με ένα, τότε
παίρνουμε τη σωστή ισότητα, που σημαίνει ότι x ίσον ένα είναι η ρίζα της εξίσωσης.

Αν το x είναι μηδέν, τότε η τετραγωνική ρίζα του μείον ένα είναι απροσδιόριστη.
Αυτό σημαίνει ότι το x ίσο με μηδέν είναι μια ξένη ρίζα.
Απάντηση: ένα.
Εργασία 4
Λύστε τον λογάριθμο της εξίσωσης της παράστασης x τετράγωνο συν πέντε x συν δύο βάση δύο ισούται με τρία.
Λύση
Ας βρούμε την εξίσωση ODZ. Για να γίνει αυτό, λύνουμε την ανισότητα x στο τετράγωνο συν πέντε x συν δύο έναντι του μηδενός.
Λύνουμε την ανισότητα με τη μέθοδο του διαστήματος. Για να γίνει αυτό, παραγοντοποιούμε την αριστερή πλευρά του, έχοντας προηγουμένως λύσει την τετραγωνική εξίσωση και λαμβάνοντας υπόψη το πρόσημο της ανισότητας, προσδιορίζουμε το ODZ. Το ODZ είναι ίσο με την ένωση των ανοιχτών ακτίνων από το μείον άπειρο στο μείον το κλάσμα πέντε συν την τετραγωνική ρίζα του δεκαεπτά διαιρούμενο με δύο, και από μείον το κλάσμα πέντε μείον την τετραγωνική ρίζα του δεκαεπτά διαιρούμενο με το δύο στο συν άπειρο.
Τώρα ας αρχίσουμε να βρίσκουμε τις ρίζες της εξίσωσης. Δεδομένου ότι το τρία είναι ίσο με τον λογάριθμο του οκτώ στη βάση δύο, γράφουμε την εξίσωση ως εξής: ο λογάριθμος της παράστασης x τετράγωνο συν πέντε x συν δύο στη βάση δύο είναι ίσος με τον λογάριθμο του οκτώ στη βάση δύο. Ας δυναμώσουμε την εξίσωση, πάρουμε και λύσουμε μια εξίσωση δευτεροβάθμιας.
Η διάκριση είναι σαράντα εννέα.
Υπολογίστε τις ρίζες:
Το x πρώτο είναι ίσο με μείον έξι. x δευτερόλεπτο ισούται με ένα.
Εξέταση
Το μείον έξι ανήκει στο ODZ, το ένα ανήκει στο ODZ, που σημαίνει ότι και οι δύο αριθμοί είναι ρίζες της εξίσωσης.
Απάντηση: μείον έξι? ένας.
Στο τελευταίο μάθημα εξετάσαμε το θέμα της εμφάνισης ξένων ριζών. Μπορούμε να τα εντοπίσουμε μέσω επαλήθευσης. Είναι δυνατόν να χάσετε ρίζες όταν λύνετε μια εξίσωση και πώς να το αποτρέψετε;
Κατά την εκτέλεση τέτοιων ενεργειών σε μια εξίσωση, όπως, πρώτον, η διαίρεση και των δύο πλευρών της εξίσωσης με την ίδια έκφραση ax από το x (εκτός από εκείνες τις περιπτώσεις που είναι σίγουρο ότι ο άξονας από το x δεν είναι ίσος με μηδέν για οποιοδήποτε x από το πεδίο ορισμού της εξίσωσης) ;
Δεύτερον, η στένωση του OD της εξίσωσης κατά τη διαδικασία επίλυσης μπορεί να οδηγήσει σε απώλεια των ριζών της εξίσωσης.
Θυμάμαι!

Η εξίσωση γράφεται ως
Το ef από το x πολλαπλασιαζόμενο με τέφρα από το x είναι ίσο με το zhe από το x πολλαπλασιασμένο με τέφρα από το x λύνεται με αυτόν τον τρόπο:
Πρέπει να παραγοντοποιήσετε βάζοντας τον κοινό παράγοντα εκτός παρενθέσεων.
Στη συνέχεια, εξισώστε κάθε παράγοντα με μηδέν, λαμβάνοντας έτσι δύο εξισώσεις.
Υπολογίζουμε τις ρίζες τους.
Ασκηση 1
Λύστε την εξίσωση x κύβος ίσον x.
Πρώτος τρόπος
Διαιρέστε και τις δύο πλευρές αυτής της εξίσωσης με το x, παίρνουμε x τετράγωνο ίσο με ένα, έχοντας ρίζες x πρώτα ίσο με ένα,
Το x δευτερόλεπτο είναι ίσο με μείον ένα.
Δεύτερος τρόπος
Ο κύβος Χ ισούται με Χ. Ας μετακινήσουμε το x στην αριστερή πλευρά της εξίσωσης, αφαιρούμε το x από αγκύλες και παίρνουμε: το x πολλαπλασιαζόμενο με το x στο τετράγωνο μείον το ένα ισούται με μηδέν.
Ας υπολογίσουμε τις ρίζες του:
Το Χ πρώτο είναι ίσο με μηδέν, το x δεύτερο είναι ίσο με ένα, το Χ τρίτο είναι ίσο με μείον ένα.
Η εξίσωση έχει τρεις ρίζες.
Όταν λύναμε την πρώτη μέθοδο, χάσαμε μια ρίζα - το x ισούται με μηδέν.
Απάντηση: μείον ένα? μηδέν; ένας.
Θυμάμαι! Η μείωση και των δύο πλευρών της εξίσωσης με έναν παράγοντα που περιέχει το άγνωστο μπορεί να οδηγήσει σε χαμένες ρίζες.
Εργασία 2
Λύστε την εξίσωση: ο δεκαδικός λογάριθμος του x στο τετράγωνο είναι ίσος με δύο.
Λύση
Πρώτος τρόπος
Με τον ορισμό ενός λογάριθμου, παίρνουμε την τετραγωνική εξίσωση x τετράγωνο ισούται με εκατό.
Οι ρίζες του: x πρώτα ισούται με δέκα. Το Χ δευτερόλεπτο ισούται με μείον δέκα.
Δεύτερος τρόπος
Με την ιδιότητα των λογαρίθμων, έχουμε δύο δεκαδικούς λογάριθμους x ίσον δύο.
Η ρίζα του - x ισούται με δέκα

Με τη δεύτερη μέθοδο, η ρίζα x ισούται με μείον δέκα χάθηκε. Και ο λόγος είναι ότι εφάρμοσαν λάθος τύπο, περιορίζοντας το εύρος της εξίσωσης. Η έκφραση για τον δεκαδικό λογάριθμο του x στο τετράγωνο ορίζεται για όλα τα x εκτός από το x ίσο με μηδέν. Η έκφραση για τον δεκαδικό λογάριθμο του x είναι για x μεγαλύτερη από το μηδέν. Ο σωστός τύπος για τον δεκαδικό λογάριθμο x τετράγωνο είναι ίσος με δύο δεκαδικούς λογάριθμους ενότητα x.
Θυμάμαι! Όταν λύνετε μια εξίσωση, χρησιμοποιήστε τους διαθέσιμους τύπους με σύνεση.
Βασικές μέθοδοι επίλυσης εξισώσεων
Ποια είναι η λύση μιας εξίσωσης;
Πανομοιότυπη μεταμόρφωση. Βασικός
τύπους μετασχηματισμών ταυτότητας.
Ξένη ρίζα. Απώλεια ρίζας.
Επίλυση της εξίσωσης είναι μια διαδικασία που αποτελείται κυρίως από την αντικατάσταση μιας δεδομένης εξίσωσης με μια άλλη εξίσωση που είναι ισοδύναμη με αυτήν . Αυτή η αντικατάσταση ονομάζεταιταυτόσημη μεταμόρφωση . Οι κύριοι μετασχηματισμοί ταυτότητας είναι οι εξής:
1.
Αντικατάσταση μιας έκφρασης με μια άλλη που είναι πανομοιότυπη με αυτήν. Για παράδειγμα, η εξίσωση (3 x+ 2 ) 2 = 15 x+ 10 μπορεί να αντικατασταθεί από το ακόλουθο ισοδύναμο:9 Χ 2 + 12 x+ 4 = 15 x+ 10 .
2.
Μεταφορά όρων μιας εξίσωσης από τη μια πλευρά στην άλλη με αντίστροφο πρόσημο. Έτσι, στην προηγούμενη εξίσωση μπορούμε να μεταφέρουμε όλους τους όρους του από τη δεξιά πλευρά προς τα αριστερά με το σύμβολο «-»: 9 Χ 2 + 12 x+ 4 – 15 Χ - 10 = 0, μετά από το οποίο παίρνουμε:9 Χ 2 – 3 Χ - 6 = 0 .
3.
Πολλαπλασιασμός ή διαίρεση και των δύο πλευρών μιας εξίσωσης με την ίδια έκφραση (αριθμό) εκτός από το μηδέν. Αυτό είναι πολύ σημαντικό γιατίη νέα εξίσωση μπορεί να μην είναι ισοδύναμη με την προηγούμενη αν η παράσταση που πολλαπλασιάζουμε ή διαιρούμε με μπορεί να είναι ίση με μηδέν.
ΠΑΡΑΔΕΙΓΜΑ Η εξίσωσηΧ - Το 1 = 0 έχει μία ρίζαx = 1.
Πολλαπλασιάζοντας και τις δύο πλευρές μεΧ - 3 , παίρνουμε την εξίσωση
( Χ - 1)( Χ - 3) = 0, που έχει δύο ρίζες:x = 1 καιΧ = 3.
Η τελευταία τιμή δεν είναι η ρίζα της δεδομένης εξίσωσης
Χ - 1 = 0. Αυτό είναι το λεγόμενοεξωγενής ρίζα .
Αντίθετα, η διαίρεση μπορεί να οδηγήσει σεαπώλεια ρίζας . Έτσι
στην περίπτωσή μας, αν (Χ - 1 )( Χ - 3 ) = 0 είναι το πρωτότυπο
εξίσωση και μετά η ρίζαx = Το 3 θα χαθεί στη διαίρεση
και στις δύο πλευρές της εξίσωσηςΧ - 3 .
Στην τελευταία εξίσωση (στοιχείο 2), μπορούμε να διαιρέσουμε όλους τους όρους της με το 3 (όχι με το μηδέν!) και τελικά να πάρουμε:
3 Χ 2 - Χ - 2 = 0 .
Αυτή η εξίσωση είναι ισοδύναμη με την αρχική:
(3 x+ 2) 2 = 15 x+ 10 .
4.
Μπορώσηκώστε και τις δύο πλευρές της εξίσωσης σε περιττή ισχύ ήεξάγετε την περιττή ρίζα και από τις δύο πλευρές της εξίσωσης . Είναι απαραίτητο να θυμάστε ότι:
α) κατασκευή σεακόμη και πτυχίο μπορεί να προκαλέσειστην απόκτηση ξένων ριζών ;
σι)λανθασμένος εξαγωγήακόμη και ρίζα μπορεί να οδηγήσει σεαπώλεια ριζών .
ΠΑΡΑΔΕΙΓΜΑΤΑ. Εξίσωση 7Χ = 35 έχει μια ενιαία ρίζαΧ = 5 .
Τετραγωνίζοντας και τις δύο πλευρές αυτής της εξίσωσης, παίρνουμε
η εξίσωση:
49 Χ 2 = 1225 .
έχει δύο ρίζες:Χ = 5 ΚαιΧ = – 5. Τελευταία τιμή
είναι μια ξένη ρίζα.
Ανακριβής παίρνοντας την τετραγωνική ρίζα και των δύο
μέρη της εξίσωσης 49Χ 2 = 1225 αποτελέσματα σε 7Χ = 35,
και χάνουμε τις ρίζες μαςΧ = – 5.
Σωστός λαμβάνοντας την τετραγωνική ρίζα έχει ως αποτέλεσμα
εξίσωση: | 7Χ | = 35, ΕΝΑ άρα σε δύο περιπτώσεις:
1) 7 Χ = 35, ΕπειταΧ = 5 ; 2) – 7 Χ = 35, ΕπειταΧ = – 5 .
Επομένως, ότανσωστός εξαγωγή τετραγώνου
ρίζες δεν χάνουμε τις ρίζες της εξίσωσης.
Τι σημαίνεισωστά εξαγάγετε τη ρίζα; Εδώ συναντιόμαστε
με μια πολύ σημαντική έννοιααριθμητική ρίζα
(εκ. ).
 Βιογραφία Manikhas Georgy Moiseevich
Βιογραφία Manikhas Georgy Moiseevich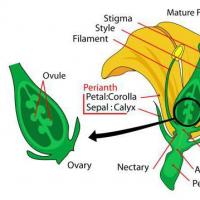 Η βοτανική είναι κλάδος της φυτοεπιστήμης
Η βοτανική είναι κλάδος της φυτοεπιστήμης Ο πιο αποτελεσματικός πρωινός διαλογισμός, συμβουλές για το πώς να κάνετε διαλογισμό το πρωί
Ο πιο αποτελεσματικός πρωινός διαλογισμός, συμβουλές για το πώς να κάνετε διαλογισμό το πρωί Πώς χρησιμοποιείται το νερό από τις επτά εκκλησίες;
Πώς χρησιμοποιείται το νερό από τις επτά εκκλησίες; Αφαίρεση ζημιάς από εκκλησία: η δύναμη του Κυρίου θα σας απαλλάξει από μια δυνατή κατάρα
Αφαίρεση ζημιάς από εκκλησία: η δύναμη του Κυρίου θα σας απαλλάξει από μια δυνατή κατάρα Πώς να αφαιρέσετε την αρνητικότητα από τον εαυτό σας στο σπίτι: αποτελεσματικοί τρόποι
Πώς να αφαιρέσετε την αρνητικότητα από τον εαυτό σας στο σπίτι: αποτελεσματικοί τρόποι