Ekvation för den approximativa räta linjen. Metoder för att approximera egenskaperna hos icke-linjära element. Mycket exakt, vacker ersättning av tabelldata med en enkel ekvation
Linjär, särskilt linjär polynom, approximation motsvarar ofta inte funktionens natur. Till exempel växer ett polynom av hög grad snabbt och därför är även en enkel funktion dåligt approximerad av polynomet på ett stort segment. Eftersom approximationen utförs över ett brett spektrum av förändringar i argumentet, är användningen av ett olinjärt beroende av koefficienterna ännu mer fördelaktigt här än med interpolation.
I praktiken används två typer av beroenden. Det ena är ett kvasilinjärt beroende, reducerat genom en utjämningsändring av variabler till ett linjärt, vilket studerades i detalj i de föregående styckena. Denna metod är mycket effektiv och används ofta vid bearbetning av experiment, eftersom a priori information om processens fysik hjälper till att hitta en bra ersättning av variabler. Vi behöver bara komma ihåg att den approximation som är bäst i de nya variablerna inte kommer att vara den bästa i betydelsen av skalärprodukten i de gamla variablerna. Därför måste särskild uppmärksamhet ägnas åt valet av vikter i nya variabler.
Ett klassiskt exempel är problemet med det radioaktiva sönderfallet av ett bestrålat prov, där de bekväma variablerna och t, där är sönderfallshastigheten. I dessa variabler är kurvan vanligtvis approximerad av en streckad linje, vars länkar motsvarar sönderfallet av allt längre livslängd medlemmar av den radioaktiva serien.
En annan vanlig typ av beroende av koefficienter är bråk-linjär, när den approximerande funktionen är rationell:
Förhållandet mellan generaliserade polynom används också ofta. Denna approximation tillåter oss att förmedla funktionens poler - de motsvarar nollorna i nämnaren för den erforderliga multipliciteten. Det är ofta möjligt att reproducera det asymptotiska beteendet vid på grund av lämpligt val av kvantitet, till exempel om , då måste vi ställa in . I det här fallet kan du ta dem tillräckligt stora för att ha många approximationskoefficienter.
Det kvadratiska felet kommer dock inte längre att vara en kvadratisk funktion av koefficienterna, så det är inte lätt att hitta koefficienterna för en rationell funktion. I analogi med rot-medelkvadratapproximationen med polynom kan vi anta att felet har ett antal nollor som inte är mindre än antalet fria koefficienter (jämför med anmärkning 3 i stycke 2). Sedan reduceras problemet till lagrangisk interpolation över dessa nollor och koefficienterna hittas från ett system av linjära ekvationer:
Naturligtvis är den exakta positionen för nollorna okänd; de väljs slumpmässigt, vanligtvis jämnt fördelade över segmentet. Denna metod kallas den valda poängmetoden. Den approximation som erhålls med denna metod kommer inte att vara den bästa alls.
Dessutom är metoden för valda punkter orimlig, liksom all interpolering om den har ett märkbart fel.
Den bästa approximationen kan hittas med den itererade viktmetoden. Observera att uppgiften
är lätt att lösa: uttrycket till vänster är en kvadratisk funktion av koefficienterna och differentiering med avseende på dem leder till ett linjärt system för att bestämma koefficienterna, liknande (38). Det nya problemet skiljer sig väsentligt från det ursprungliga genom att en annan vikt används istället för en vikt, så dess lösning är inte den bästa approximationen. Låt oss skriva det ursprungliga problemet i en ny form:

och vi kommer att lösa det genom en enkel iterativ process

kan tas som nollapproximationen. Vid varje iteration är vikten känd från den tidigare iterationen, så koefficienterna kan lätt hittas från kvadratformens minimivillkor. Övning visar att koefficienterna för den bästa approximationen svagt beror på valet av vikt, så iterationerna konvergerar vanligtvis snabbt.
a) Betrakta några exempel på approximation med en rationell funktion. Låt oss sätta
genom att ersätta de två första termerna i serien med ett bråk får vi . Denna enkla formel säkerställer noggrannhet vid och är mycket bekväm för uppskattningar.
b) I sannolikhetsteorin spelar en viktig roll av felintegralen för vilken serieexpansion är kända:

Den första serien konvergerar absolut, men vid konvergens är den mycket långsam; den andra serien konvergerar asymptotiskt för stora värden på . Genom att ersätta de första termerna i varje serie med bråk får vi

I de angivna intervallen för argumentändring överstiger inte felet för den första formeln 0,4 % och felet för den andra formeln inte överstiger 2,4 %. Sålunda är noggrannheten hos dessa approximationer ganska tillräcklig för många praktiska tillämpningar.
c) Låt oss ställa in på . Denna funktion är monoton, och för Det är lätt att konstruera ett bråk
![]()
Approximation av en icke-linjär funktion
x 0 /12 /6 /4 /3 5/12 /2
y 0,5 0,483 0,433 0,354 0,25 0,129 0
Eftersom intervallet för uppdelning av funktionen är lika, beräknar vi följande lutningskoefficienter för motsvarande sektioner av den approximerade funktionen:

1. Konstruktion av block för att bilda segment av den approximerande funktionen
Bildandet av tidsfunktionen
Ändringsintervall:
Cyklisk återstartstid: T = 1s
Låt oss nu modellera funktionen:

Approximation


Figur 3.1 - Schema för att lösa ekvationen
Figur 3.2 - Blockschema över bildandet av en olinjär funktion
Således bildas den vänstra sidan av ekvationen automatiskt. I detta fall antas det konventionellt att den högsta derivatan x// är känd, eftersom termerna på höger sida av ekvationen är kända och kan kopplas till ingångarna till U1 (Figur 3.1). Operationsförstärkaren U3 fungerar som en +x signalväxelriktare. För att simulera x// är det nödvändigt att införa ytterligare en delförstärkare i kretsen, till vars ingångar det är nödvändigt att leverera signaler som simulerar den högra sidan av ekvationen (3.2).
Skalorna för alla variabler beräknas med hänsyn till att maxvärdet för maskinvariabeln bortom det absoluta värdet är 10 V:
Mx = 10/xmax; Mx/ = 10/x/max; Mx // = 10 / x //max;
My = 10 / ymax. (3.3)
Tidsskala Mt = T / tmax = 1, eftersom problemet simuleras i realtid.
Överföringskoefficienterna för varje ingång hos de integrerande förstärkarna beräknas.
För förstärkare U1 hittas överföringskoefficienterna med formlerna:
K11 = Mx/b/(MyMt); K12 = Mx/a2/(MxMt);
K13 = Mx/a1/(MxMt). (3.4)
För förstärkare U2:
K21 = Mx/ / (Mx/ Mt), (3,5)
och för förstärkare U3:
K31 = 1. (3,6)
Spänningarna för de initiala förhållandena beräknas med hjälp av formlerna:
ux/(0) = Mx/x/(0) (-1); ux(0)= Mxx(0) (+1). (3,7)
Den högra sidan av ekvation (3.2) representeras av en olinjär funktion, som specificeras av linjär approximation. I det här fallet är det nödvändigt att kontrollera att approximationsfelet inte överstiger ett specificerat värde. Blockschemat för bildandet av en icke-linjär funktion presenteras i figur 3.2.
Beskrivning av kretsschemat
Blocket för att generera tidsfunktionen (Ф) är gjort i form av en (för att bilda t) eller två seriekopplade (för att bilda t2) integrerande förstärkare med noll initiala villkor.
I det här fallet, när en signal U appliceras på ingången till den första integratorn, får vi vid dess utgång:
u1(t)= -K11 = -K11Et. (3,8)
Inställning K11E=1 har vi u1(t)= t.
Vid utgången av den andra integratorn får vi:
u2(t)= K21 = K11K21Et2 / 2 (3,9)
Inställning K11K21E/2 = 1, vi har u2(t)= t2.
Block för att bilda segment av den approximerande funktionen är implementerade i form av diodblock av olinjära funktioner (DBNF), vars ingångsvärde är en funktion av tiden t eller t2. Proceduren för att beräkna och konstruera DBNF ges i.
Adderaren (SAD) av segment av den approximerande funktionen utförs i form av en differentiell slutförstärkare.
De initiala villkoren för integratörerna av modelleringskretsen introduceras med hjälp av en nod med en variabel struktur (Figur 3.3). Detta schema kan fungera i två lägen:
a) integration - med nyckel K i position 1. I detta fall beskrivs kretsens initialsignal med tillräcklig noggrannhet med ekvationen för en ideal integrator:
u1(t)= - (1 / RC) . (3,10)
Detta läge används vid modellering av en uppgift. För att kontrollera korrektheten av valet av parametrar R och C för integratorn, kontrollera värdet på integratorns initialspänning som en funktion av tiden och den användbara integrationstiden inom det tillåtna felet?
Storleken på den initiala integratorspänningen
U(t)= - KYE (1 - e - T / [(Ky+1)RC) (3.11)
under simuleringen bör T när ingångssignalen E integreras med en operationsförstärkare med en förstärkning Ky utan återkopplingskrets inte överstiga värdet på maskinvariabeln (10 V).
Integrationstid
Ti = 2RC(Kу + 1)?Uadd (3.12)
med de valda kretsparametrarna bör inte vara mindre än simuleringstiden T.
b) inställning av de initiala villkoren implementeras när nyckel K växlas till läge 2. Detta läge används när modelleringskretsen förbereds för lösningsprocessen. I detta fall beskrivs kretsens ursprungliga signal med ekvationen:
u0(t)= - (R2/R1) E (3,13)
där u0(t) är värdet av initialvillkoren.
För att minska tiden för bildandet av initiala förhållanden och säkerställa tillförlitlig drift måste kretsparametrarna uppfylla villkoret: R1C1 = R2C.
Konstruera ett komplett beräkningsschema. I det här fallet bör du använda symbolerna i underavsnitt 3.1.
Använd bitdjupet för indata och källdata, konstruera kretsscheman för blocken B1 och B2 och anslut dem till RS-blocket.
(Observera det ytterligare avsnittet daterat 06/04/2017 i slutet av artikeln.)
Redovisning och kontroll! De över 40 borde väl komma ihåg denna slogan från eran av att bygga socialism och kommunism i vårt land.
Men utan väletablerad bokföring är det omöjligt att fungera effektivt för ett land, en region, ett företag eller ett hushåll i någon socioekonomisk samhällsform! För att upprätta prognoser och planer för aktivitet och utveckling krävs initiala underlag. Var kan jag få tag i dem? Bara en pålitlig källan är din statistiska register över tidigare tidsperioder.
Enligt min uppfattning bör varje vettig person ta hänsyn till resultaten av sina aktiviteter, samla in och registrera information, bearbeta och analysera data och tillämpa analysresultaten för att fatta rätt beslut i framtiden. Detta är inget annat än ackumulering och rationell användning av ens livserfarenhet. Om du inte sparar viktiga data kommer du efter en viss tid att glömma dem och när du börjar ta itu med dessa problem igen kommer du igen att göra samma misstag som du gjorde när du först gjorde detta.
"Jag minns att vi för 5 år sedan producerade upp till 1000 stycken av sådana produkter per månad, och nu kan vi knappt montera 700!" Vi öppnar statistiken och ser att för 5 år sedan tillverkade de inte ens 500 stycken...
”Hur mycket kostar en kilometer av din bil, med hänsyn tagen alla kostar? Låt oss öppna statistiken - 6 rubel/km. Resa till jobbet - 107 rubel. Billigare än att ta en taxi (180 rubel) mer än en och en halv gånger. Och det fanns tillfällen då det var billigare att ta en taxi...
"Hur lång tid tar det att tillverka stålkonstruktionerna i ett 50 meter högt hörnkommunikationstorn?" Vi öppnar statistiken – och om 5 minuter är svaret klart...
"Hur mycket kommer det att kosta att renovera ett rum i en lägenhet?" Vi drar upp gamla rekord, gör en justering för inflationen under de senaste åren, tar hänsyn till att vi förra gången köpte material 10% billigare än marknadspriset och vi vet redan den beräknade kostnaden...
Genom att föra register över dina yrkesaktiviteter kommer du alltid att vara redo att svara på din chefs fråga: "När!!!???" Genom att föra hushållsjournaler är det lättare att planera utgifter för stora inköp, semester och andra utgifter i framtiden, vidta lämpliga åtgärder för att tjäna extra inkomster eller minska onödiga utgifter idag.
I den här artikeln kommer jag att använda ett enkelt exempel för att visa hur insamlad statistisk data kan bearbetas i Excel för vidare användning vid prognostisering av framtida perioder.
Approximation av statistisk data i Excel med en analytisk funktion.
Produktionsplatsen producerar byggnadsmetallkonstruktioner av plåt- och profilprodukter. Sajten fungerar stabilt, beställningarna är av samma typ, antalet arbetare fluktuerar något. Det finns uppgifter om produktproduktion för de föregående 12 månaderna och om mängden valsad metall som bearbetats under dessa tidsperioder per grupp: plåt, I-balkar, kanaler, vinklar, runda rör, rektangulära profiler, runda produkter. Efter en preliminär analys av de initiala uppgifterna uppstod ett antagande att den totala månatliga produktionen av metallkonstruktioner väsentligt beror på antalet vinklar i beställningar. Låt oss kontrollera detta antagande.
Först och främst några ord om approximation. Vi kommer att leta efter en lag - en analytisk funktion, det vill säga en funktion specificerad av en ekvation som bättre än andra beskriver beroendet av den totala produktionen av metallstrukturer på mängden vinkelstål i slutförda beställningar. Detta är en approximation, och den hittade ekvationen kallas approximationsfunktionen för den ursprungliga funktionen, given i form av en tabell.
1. Slå på Excel och placera en tabell med statistikdata på ett ark.

2. Därefter bygger och formaterar vi ett spridningsdiagram, där vi längs X-axeln ställer in värdena för argumentet - antalet bearbetade hörn i ton. Längs Y-axeln plottar vi värdena för den ursprungliga funktionen - den totala produktionen av metallstrukturer per månad, specificerad i tabellen.

3. Vi "pekar" med musen på någon av punkterna på diagrammet och högerklickar för att ta fram snabbmenyn (som en av mina goda vänner säger - när du arbetar i ett okänt program, när du inte vet vad du ska göra, klicka på höger musknapp oftare...). I rullgardinsmenyn väljer du "Lägg till trendlinje...".
4. I fönstret "Trendlinje" som visas, på fliken "Typ", välj "Linjär".


6. En rät linje dök upp på grafen, som approximerade vårt tabellberoende.

Förutom själva linjen ser vi ekvationen för denna linje och, viktigast av allt, vi ser värdet på parametern R 2 - värdet på tillförlitligheten för approximationen! Ju närmare dess värde är 1, desto mer exakt approximerar den valda funktionen tabelldata!
7. Vi bygger trendlinjer med hjälp av potens-, logaritmiska, exponentiella och polynomiska approximationer på samma sätt som vi byggde en linjär trendlinje.

Av alla de valda funktionerna, approximerar ett polynom av andra graden vår data bäst, det har den maximala tillförlitlighetskoefficienten R 2 .
Jag vill dock varna dig! Om du tar polynom av högre grader kommer du förmodligen att få ännu bättre resultat, men kurvorna kommer att få ett invecklat utseende... Det är viktigt att förstå här att vi letar efter en funktion som har fysisk betydelse. Vad betyder det här? Detta innebär att vi behöver en approximativ funktion som kommer att ge adekvata resultat inte bara inom det övervägda intervallet av X-värden, utan också utanför det, det vill säga den kommer att svara på frågan: "Vad blir resultatet av metallstrukturer om antalet bearbetade vinklar per månad är mindre än 45 och mer än 168 ton! Därför rekommenderar jag inte att låta dig ryckas med polynom av höga grader, och att välja en parabel (polynom av andra graden) noggrant!
Så vi måste välja en funktion som inte bara interpolerar väl tabelldata inom intervallet för värden X = 45...168, utan också tillåter adekvat extrapolering utanför detta intervall. I det här fallet väljer jag en logaritmisk funktion, även om du också kan välja en linjär, eftersom den är den enklaste. I exemplet under övervägande, när du väljer en linjär approximation i Excel, kommer felen att vara större än när du väljer en logaritmisk, men inte mycket.
8. Vi tar bort alla trendlinjer från diagramfältet, förutom den logaritmiska funktionen. För att göra detta, högerklicka på onödiga rader och välj "Rensa" från snabbmenyn som visas.
9. Slutligen kommer vi att lägga till felstaplar till datapunkterna i tabellform. För att göra detta, högerklicka på någon av punkterna på grafen och välj "Formatera dataserie..." i snabbmenyn och konfigurera data på fliken "Y-fel" som i figuren nedan.

10. Högerklicka sedan på någon av felintervallslinjerna, välj "Formatera felfält..." i snabbmenyn och i fönstret "Formatera felfält" på fliken "Visa", justera färgen och tjockleken på linjerna.

Alla andra diagramobjekt formateras på samma sätt.Excel!
Det slutliga resultatet av diagrammet visas i följande skärmdump.

Resultat.
Resultatet av alla tidigare åtgärder var den resulterande formeln för den approximativa funktionen y=-172,01*ln (x)+1188,2. Genom att veta det, och antalet hörn i den månatliga uppsättningen av arbeten, är det möjligt med en hög grad av sannolikhet (±4% - se felstaplar) att förutsäga den totala produktionen av metallstrukturer för månaden! Till exempel, om planen för månaden är 140 ton vinklar, kommer den totala produktionen, allt annat lika, troligen att vara 338 ± 14 ton.
För att öka tillförlitligheten av approximationen bör det finnas mycket statistisk data. Tolv par av värden är inte tillräckligt.
Från praktiken kommer jag att säga att att hitta en approximerande funktion med en tillförlitlighetskoefficient R 2 >0,87 bör betraktas som ett bra resultat. Ett utmärkt resultat är med R2 >0,94.
I praktiken kan det vara svårt att identifiera en viktigast avgörande faktor (i vårt exempel, mängden hörn som bearbetas under en månad), men om du försöker kan du alltid hitta den i varje specifik uppgift! Naturligtvis beror den totala produktionen för en månad verkligen på hundratals faktorer, med hänsyn till vilket kräver betydande arbetskostnader från standardsättare och andra specialister. Men resultatet blir ändå ungefärligt! Så är det värt att ta på sig kostnaderna när det finns mycket billigare matematisk modellering!
I den här artikeln har jag bara berört toppen av ett isberg som kallas insamling, bearbetning och praktisk användning av statistiska data. Jag hoppas få reda på om jag lyckades eller inte väcka ditt intresse för detta ämne från kommentarerna och betygen av artikeln i sökmotorer.
Den uppkomna frågan om att approximera en funktion av en variabel har bred praktisk tillämpning inom olika områden av livet. Men lösningen på har mycket större tillämpning flera oberoende variabler... Läs om detta och mer i följande bloggartiklar.
Prenumerera till meddelanden om artiklar i fönstret som finns i slutet av varje artikel eller i fönstret högst upp på sidan.
Glöm inte bekräfta prenumerera genom att klicka på länken i ett brev som kommer till dig på angiven post (kan komma in i mappen « Spam » )!!!
Jag kommer att läsa dina kommentarer med intresse, kära läsare! Skriva!
P.S. (06/04/2017)
Mycket exakt, vacker ersättning av tabelldata med en enkel ekvation.
Du är inte nöjd med den erhållna approximationsnoggrannheten (R 2<0,95) или вид и набор функций, предлагаемые MS Excel?
Är dimensionerna på uttrycket och linjeformen för det höggradiga approximerande polynomet inte tilltalande för ögat?
Se sidan "" för att få ett mer exakt och kompakt resultat av approximation av dina tabelldata och för att lära dig en enkel teknik för att lösa problem med högprecisionsapproximation med en funktion av en variabel.

När man använde den föreslagna algoritmen för åtgärder fann man en mycket kompakt funktion som ger den högsta noggrannheten av approximation: R 2 =0,9963!!!
Numeriska metoder för att lösa problem
Radiofysik och elektronik
(Handledning)
Voronezh 2009
Läroboken utarbetades vid institutionen för fysisk elektronik
Fakulteten vid Voronezh State University.
Metoder för att lösa problem i samband med automatiserad analys av elektroniska kretsar övervägs. De grundläggande begreppen grafteorin presenteras. En matris-topologisk formulering av Kirchhoffs lagar ges. De mest välkända matristopologiska metoderna beskrivs: metoden för nodpotentialer, metoden för slingströmmar, metoden för diskreta modeller, hybridmetoden, metoden för variabla tillstånd.
1. Approximation av olinjära egenskaper. Interpolation. 6
1.1. Newton och Lagrange polynom 6
1.2. Spline-interpolation 8
1.3. Minsta kvadraters metod 9
2. System av algebraiska ekvationer 28
2.1. System av linjära ekvationer. Gauss metod. 28
2.2. Glesa ekvationssystem. LU-faktorisering. 36
2.3. Lösa olinjära ekvationer 37
2.4. Lösa system av icke-linjära ekvationer 40
2.5. Differentialekvationer. 44
2. Metoder för att söka efter extremum. Optimering. 28
2.1. Extrema sökmetoder. 36
2.2. Passiv sökning 28
2.3. Sekventiell sökning 36
2.4. Flerdimensionell optimering 37
Referenser 47
Approximation av olinjära egenskaper. Interpolation.
1.1. Newton och Lagrange polynom.
När man löser många problem blir det nödvändigt att ersätta en funktion f, om vilken det finns ofullständig information eller vars form är för komplex, med en enklare och bekvämare funktion F, nära f i en eller annan mening, vilket ger dess ungefärliga representation. För approximation (approximation) används funktioner F som tillhör en viss klass, till exempel algebraiska polynom av en given grad. Det finns många olika versioner av, beroende på vilka funktioner f som är approximerade, vilka funktioner F som används för approximation, hur närheten till funktioner f och F förstås osv.
En av metoderna för att konstruera approximativa funktioner är interpolation, när det krävs att vid vissa punkter (interpolationsnoder) sammanfaller värdena för den ursprungliga funktionen f och den approximerande funktionen F. I det mer allmänna fallet är värdena på derivatan vid givna punkter måste sammanfalla.
Funktionsinterpolation används för att ersätta en svårberäknad funktion med en annan som är lättare att beräkna; för ungefärlig återställning av en funktion från dess värden vid enskilda punkter; för numerisk differentiering och integration av funktioner; för numerisk lösning av olinjära och differentialekvationer, etc.
Det enklaste interpolationsproblemet är som följer. För en viss funktion på ett segment anges n+1 värden vid punkter, som kallas interpolationsnoder. Vart i . Det krävs att man konstruerar en interpoleringsfunktion F(x) som tar samma värden vid interpolationsnoderna som f(x):
F(x 0) = f(x 0), F(x 1) = f(x 1), ... , F(x n) = f(x n)
Geometriskt betyder detta att man hittar en kurva av en viss typ som går genom ett givet system av punkter (xi, y i), i = 0,1,...,n.
Om värdena för argumentet går utanför regionen, pratar vi om extrapolering - fortsättningen av funktionen bortom regionen för dess definition.
Oftast är funktionen F(x) konstruerad i form av ett algebraiskt polynom. Det finns flera representationer av algebraiska interpolationspolynom.
En av metoderna för att interpolera funktioner som tar värden vid punkter är att konstruera ett Lagrangepolynom, som har följande form:
Graden av interpolationspolynomet som passerar genom n+1 interpolationsnoder är lika med n.
Av formen av Lagrangepolynomet följer att lägga till en ny nodalpunkt leder till en förändring i alla termer av polynomet. Detta är besväret med Lagranges formel. Men Lagrange-metoden innehåller ett minsta antal aritmetiska operationer.
För att konstruera Lagrangepolynom med ökande grader kan följande iterationsschema (Aitken-schema) användas.
Polynom som passerar genom två punkter (xi, y i), (x j, y j) (i=0,1,...,n-1; j=i+1,...,n) kan representeras enligt följande:
Polynom som passerar genom tre punkter (xi, y i), (x j, y j), (x k, y k)
(i=0,…,n-2; j=i+1,…,n-1; k=j+1,…,n), kan uttryckas genom polynomen Lij och Ljk:
Polynom för fyra punkter (xi, y i), (x j, y j), (x k, y k), (x l, y l) är konstruerade från polynomen L ijk och L jkl:
Processen fortsätter tills ett polynom erhålls som passerar genom n givna punkter.
Algoritmen för att beräkna värdet av Lagrangepolynomet vid punkt XX, implementerande Aitken-schemat, kan skrivas med operatorn:
för (int i=0;i för (int i=0;i<=N-2;i++)Здесь не нужно слово int, программа det kommer att uppfattas som ett fel - upprepad deklaration av variabeln, variabel i har redan deklarerats för (int j=i+1;j<=N-1;j++) F[j]=((arg-x[i])*F[j]-(arg-x[j])*F[i])/(x[j]-x[i]); där matris F är mellanvärdena för Lagrangepolynomet. Inledningsvis bör F[I] sättas lika med y i . Efter exekvering av looparna är F[N] värdet på Lagrangepolynomet av grad N vid punkt XX. En annan form för att representera interpolationspolynomet är Newtons formler. Låta vara ekvidistanta interpolationsnoder; i=0,1,…,n; - interpolationssteg. Newtons första interpolationsformel, som används för framåtinterpolation, är: Kallas (ändliga) i:te ordningens skillnader. De definieras så här: Normaliserat argument. När Newtons interpolationsformel förvandlas till en Taylor-serie. Newtons andra interpolationsformel används för att interpolera "bakåt": I den sista posten, istället för skillnader (kallade "framåt" skillnader), "bakåt" skillnader används: Vid ojämnt fördelade noder, den sk separerade skillnader I det här fallet har interpolationspolynomet i Newtonform formen I motsats till Lagrange-formeln lägger man till ett nytt värdepar. (x n +1, y n +1) reduceras här till tillägg av en ny term. Därför kan antalet interpolationsnoder enkelt ökas utan att hela beräkningen upprepas. Detta gör att du kan utvärdera interpolationens noggrannhet. Newtons formler kräver dock fler aritmetiska operationer än Lagranges formler. För n=1 får vi formeln för linjär interpolation: För n=2 kommer vi att ha formeln för parabolisk interpolation: Vid interpolering av funktioner används höggradiga algebraiska polynom sällan på grund av betydande beräkningskostnader och stora fel i beräkningsvärden. I praktiken används oftast bitvis linjär eller bitvis parabolisk interpolation. Med styckvis linjär interpolation approximeras funktionen f(x) på intervallet (i=0,1,...,n-1) av ett rakt linjesegment En beräkningsalgoritm som implementerar bitvis linjär interpolation kan skrivas med operatorn: för (int i=0;i if ((arg>=Fx[i]) && (arg<=Fx)) res=Fy[i]+(Fy-Fy[i])*(arg-Fx[i])/(Fx-Fx[i]); Med den första slingan letar vi efter var den önskade punkten finns. Med styckvis parabolisk interpolation konstrueras polynomet med hjälp av de 3 nodpunkterna närmast det angivna värdet för argumentet. Beräkningsalgoritmen som implementerar bitvis parabolisk interpolation kan skrivas med operatorn: för (int i=0;i y0=Fy; När i=0 finns inte elementet! x0=Fx; Det samma res=y0+(y1-y0)*(arg-x0)/(x1-x0)+(1/(x2-x0))*(arg-x0)*(arg-x1)*(((y2-y1) /(x2-xl))-((yl-y0)/(xl-x0))); Användning av interpolation är inte alltid tillrådligt. Vid bearbetning av experimentella data är det önskvärt att jämna ut funktionen. Approximation av experimentella beroenden med hjälp av minsta kvadratmetoden baseras på kravet att minimera rotmedelkvadratfelet Koefficienterna för det approximerande polynomet hittas från att lösa ett system av m+1 linjära ekvationer, de så kallade. "normala" ekvationer, k=0,1,...,m Förutom algebraiska polynom används trigonometriska polynom i stor utsträckning för att approximera funktioner (se "numerisk övertonsanalys"). Splines är ett effektivt sätt att approximera en funktion. En spline kräver att dess värden och derivator vid nodpunkter sammanfaller med den interpolerade funktionen f(x) och dess derivator upp till en viss ordning. Konstruktionen av splines kräver dock i vissa fall betydande beräkningskostnader. Låt, som ett resultat av mätningar under experimentet, en tabellformig tilldelning av en viss funktion erhållas f(x), uttrycker förhållandet mellan två geografiska parametrar: Naturligtvis kan du hitta en formel som uttrycker detta beroende analytiskt genom att använda interpolationsmetoden. Emellertid kan sammanträffandet av värdena för den erhållna analytiska specifikationen av funktionen vid interpolationsnoderna med tillgängliga empiriska data ofta inte betyda en sammanträffande av beteendet hos de ursprungliga och interpolerande funktionerna över hela observationsintervallet. Dessutom erhålls alltid geografiska indikatorers tabellberoende som ett resultat av mätningar med olika instrument som har ett visst och inte alltid tillräckligt litet mätfel. Kravet på en exakt sammanträffande av värdena för de approximerande och approximerande funktionerna vid noderna är desto mer omotiverat om funktionens värden f(x), de som erhålls som ett resultat av mätningar är själva ungefärliga. Problemet med att approximera en funktion av en variabel från allra första början tar med nödvändighet hänsyn till beteendet hos den ursprungliga funktionen över hela observationsintervallet. Formuleringen av problemet är som följer. Fungera y= f(x) ges av tabell (1). Det är nödvändigt att hitta en funktion av en given typ: som är på punkter x 1, x 2, …, x n tar värden så nära tabellerna som möjligt y 1, y 2, …, y n. I praktiken bestäms typen av approximerande funktion oftast genom att jämföra formen på den ungefär konstruerade grafen för funktionen y= f(x) med grafer över funktioner kända för forskaren, specificerade analytiskt (oftast elementära funktioner som är enkla till utseendet). Enligt tabell (1) konstrueras nämligen en punktdiagram f(x), sedan ritas en jämn kurva, som så gott som möjligt återspeglar beskaffenheten av punkternas placering. Utifrån kurvan som erhålls på detta sätt fastställs formen för approximationsfunktionen på en kvalitativ nivå. Tänk på figur 6. Figur 6 visar tre situationer: Det bör noteras att ett strikt funktionellt beroende för en tabell med initiala data sällan observeras, eftersom var och en av kvantiteterna som är involverade i den kan bero på många slumpmässiga faktorer. Men formel (2) (den kallas den empiriska formeln eller regressionsekvationen på på X) är intressant eftersom det låter dig hitta funktionens värden f för icke-tabellvärden X, "utjämna" resultaten av mätningar av kvantiteten på, dvs. genom hela skalan av förändringar X. Berättigandet av detta tillvägagångssätt bestäms i slutändan av den praktiska användbarheten av den resulterande formeln. Genom det befintliga "molnet" av punkter kan du alltid försöka dra en linje av en etablerad typ, som är den bästa i en viss mening bland alla linjer av en given typ, det vill säga "närmast" observationspunkterna i deras helhet. För att göra detta definierar vi först begreppet närhet av en linje till en viss uppsättning punkter på planet. Mått på sådan närhet kan variera. Varje rimligt mått måste dock uppenbarligen relateras till avståndet från observationspunkterna till linjen i fråga (given av ekvationen y=F(x)).
Låt oss anta att den approximerande funktionen F(x) på punkter x 1, x 2, ..., x n materia y 1 , y 2 , ..., y n. Ofta används minsta summan av kvadrerade skillnader mellan observationer av den beroende variabeln som ett närhetskriterium y i och teoretiska värden beräknade med hjälp av regressionsekvationen y i. Här tror man att y i Och x i- kända observationsdata, och F- ekvation av en regressionslinje med okända parametrar (formler för att beräkna dem kommer att ges nedan). En metod för att uppskatta parametrarna för en approximerande funktion som minimerar summan av kvadrerade avvikelser av observationer av den beroende variabeln från värdena för den önskade funktionen kallas minsta metod rutor (LS) eller Minsta kvadratmetoden (LS). Så, f kan nu formuleras enligt följande: för funktionen f, givet av tabell (1), hitta funktionen F en viss typ så att summan av kvadraterna Ф är den minsta. Låt oss överväga metoden för att hitta en approximerande funktion i allmän form med hjälp av exemplet på en approximerande funktion med tre parametrar: Låta F(xi, a, b, c) = y, i=1, 2, ..., n. Summan av kvadrerade skillnader av motsvarande värden f Och F kommer att se ut så här: Denna summa är en funktion av Ф (a, b, c) tre variabler (parametrar a, b Och c). Uppgiften handlar om att hitta sitt minimum. Vi använder det nödvändiga villkoret för ett extremum: Vi får ett system för att bestämma de okända parametrarna a, b, c. Efter att ha löst detta system med tre ekvationer med tre okända angående parametrarna a, b, c, vi kommer att få den specifika formen för den önskade funktionen F(x, a, b, c). Som framgår av exemplet kommer en förändring av antalet parametrar inte att leda till en förvrängning av själva tillvägagångssättets essens, utan kommer endast att uttryckas i en förändring av antalet ekvationer i systemet (5). Det är naturligt att förvänta sig att värdena för det hittade fungerar F(x, a, b, c) på punkter x 1, x 2, ..., x n, kommer att skilja sig från tabellvärdena y 1 , y 2 , ..., y n. Skillnadsvärden y i -F(xi,a, b, c)=ei (i=1, 2, ..., n) kallas avvikelser av uppmätta värden y från de som beräknats med formel (3). För den hittade empiriska formeln (2) i enlighet med den ursprungliga tabellen (1) är det därför möjligt att finna summan av kvadrerade avvikelser, som enligt minsta kvadratmetoden för en given typ av approximationsfunktion (och de funna parametervärdena) bör vara minst. Av två olika approximationer av samma tabellfunktion, enligt minsta kvadratmetoden, bör den bästa anses vara den för vilken summan (4) har det minsta värdet. I experimentell praktik, som approximerande funktioner beroende på arten av spridningsdiagrammet f Approximationsfunktioner med två parametrar används ofta: Uppenbarligen, när typen av approximerande funktion är etablerad, reduceras uppgiften endast till att hitta parametrarnas värden. Låt oss överväga de vanligaste empiriska beroendena i praktisk forskning. 3.3.1. Linjär funktion (linjär regression). Utgångspunkten för beroendeanalys är vanligtvis att uppskatta variablernas linjära beroende. Man bör dock ta hänsyn till att den "bästa" räta linjen med minsta kvadratmetoden alltid finns, men även den bästa är inte alltid tillräckligt bra. Om i verkligheten missbruk y=f(x)är kvadratisk, så kan ingen linjär funktion beskriva den på ett tillfredsställande sätt, även om det bland alla sådana funktioner säkert kommer att finnas en "bästa". Om värdena X Och på inte är relaterade alls, vi kan också alltid hitta den "bästa" linjära funktionen y=ax+b för en given uppsättning observationer, men i detta fall specifika värden A Och b bestäms endast av slumpmässiga avvikelser av variablerna och kommer själva att variera mycket för olika urval från samma population. Låt oss nu överväga problemet med att uppskatta linjära regressionskoefficienter mer formellt. Låt oss anta att sambandet mellan x Och yär linjär och vi kommer att leta efter den önskade approximationsfunktionen i formen: Låt oss hitta partiella derivator med avseende på parametrarna: Låt oss ersätta de erhållna relationerna i ett system av formen (5): eller dividera varje ekvation med n: Låt oss presentera följande notation: Då kommer det sista systemet att se ut så här: Koefficienterna för detta system M x , M y , M xy , M x 2- tal som i varje specifikt approximationsproblem lätt kan beräknas med formler (7), där x i, y i- värden från tabell (1). Efter att ha löst system (8) får vi parametervärdena a Och b, och därför den specifika formen av den linjära funktionen (6). Ett nödvändigt villkor för att välja en linjär funktion som den önskade empiriska formeln är relationen: 3.3.2. Kvadratisk funktion (kvadratisk regression). Vi kommer att leta efter en approximativ funktion i form av ett kvadratiskt trinomial: Hitta partiella derivator: Låt oss skapa ett system av formen (5): Efter enkla transformationer får vi ett system med tre linjära ekvationer med tre okända a, b, c. Systemets koefficienter, som i fallet med en linjär funktion, uttrycks endast genom kända data från tabell (1): Här använder vi notation (7), liksom Lösningen av system (10) ger värdet på parametrarna a, b Och Med för approximeringsfunktionen (9). Kvadratisk regression tillämpas om alla uttryck i formen y 2 -2y 1 + y 0 , y 3 -2 y 2 + y 1 , y 4 -2 y 3 + y 2 etc. skiljer sig lite från varandra.
3.3.3. Potensfunktion (geometrisk regression). Låt oss nu hitta den approximerande funktionen i formen: Om vi antar att i den ursprungliga tabellen (1) värdena för argumentet och funktionsvärdena är positiva, tar vi logaritmen för likhet (11) under villkoret a>0: Sedan funktionen Fär en approximation för funktionen f, funktion lnF kommer att vara en uppskattning för funktionen lnf. Låt oss introducera en ny variabel u=lnx; sedan, som följer av (12), lnF kommer att vara en funktion av u:
Ф(u). Låt oss beteckna Nu tar jämställdhet (12) formen: de där. problemet reducerades till att hitta en approximerande funktion i form av en linjär. I praktiken, för att hitta den önskade approximerande funktionen i form av en potensfunktion (under antagandena ovan), är det nödvändigt att göra följande: 1. Använd denna tabell (1) skapa en ny tabell med logaritmer av värdena x Och y i källtabellen; 2. använd den nya tabellen för att hitta parametrarna A Och I approximering av formens (14) funktion; 3. Använd notation (13), hitta värdena för parametrarna a Och m och ersätt dem med uttryck (11). En nödvändig förutsättning för att välja en potensfunktion som den önskade empiriska formeln är relationen: 3.3.4. Exponentiell funktion .
Låt den ursprungliga tabellen (1) vara sådan att det är tillrådligt att leta efter den approximerande funktionen i form av en exponentialfunktion: Låt oss ta logaritmen för likhet (15): Med notation (13) skriver vi om (16) i formen: För att hitta den approximerande funktionen i formen (15) är det alltså nödvändigt att logaritma funktionsvärdena i den ursprungliga tabellen (1) och, med tanke på dem tillsammans med de ursprungliga värdena för argumentet, konstruera en approximerande funktion av formuläret (17) för den nya tabellen. Efter detta, i enlighet med notation (13), återstår det att erhålla värdena för de sökta parametrarna a Och b och ersätt dem med formel (15). Ett nödvändigt villkor för att välja en exponentiell funktion som den önskade empiriska formeln är förhållandet: 3.3.5. Linjär bråkdelfunktion. Vi kommer att leta efter en ungefärlig funktion i formen: Vi skriver om jämställdhet (18) enligt följande: Av den senaste likheten följer att för att hitta parametervärdena a Och b för en given tabell (1) måste du skapa en ny tabell, där argumentvärdena lämnas desamma, och funktionsvärdena ersätts med inversa tal, och sedan för den resulterande tabellen, hitta en approximativ formens funktion yxa+b. Hittade parametervärden a Och b ersätta i formel (18). Ett nödvändigt villkor för att välja en linjär bråkdelfunktion som den önskade empiriska formeln är relationen: 3.3.6. Logaritmisk funktion. Låt approximationsfunktionen ha formen: Det är lätt att se att för att gå till en linjär funktion räcker det med att göra substitutionen lnx=u. Det följer att för att hitta värdena a Och b du måste logaritma värdena för argumentet i den ursprungliga tabellen (1) och, med tanke på de erhållna värdena i kombination med de ursprungliga värdena för funktionen, hitta en approximativ funktion i form av en linjär för den nya tabellen som sålunda erhållits. Odds a Och b ersätt den hittade funktionen i formel (19). Ett nödvändigt villkor för att välja en logaritmisk funktion som den önskade empiriska formeln är förhållandet: 3.3.7. Hyperbel. Om ett spridningsdiagram konstruerat från tabell (1) ger en gren av en hyperbel, kan den approximerande funktionen letas efter i formuläret.
1
| | | | | | | | | | | |
X
x 1
x 2
…
x n
f(x)
y 1
vid 2
…
y n
![]()
![]() (3)
(3)![]()
 (5)
(5)
![]()



 (7)
(7) (8)
(8)![]()

 (10)
(10)![]() (11)
(11)![]() (16)
(16)![]() (17)
(17) .
.
![]() (18)
(18)
 .
.![]() .
.
 Berättelsen om piloterna som bombade Hiroshima och Nagasaki
Berättelsen om piloterna som bombade Hiroshima och Nagasaki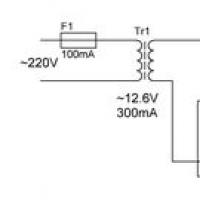 Smidig kapacitetsladdning: vad ska man välja?
Smidig kapacitetsladdning: vad ska man välja?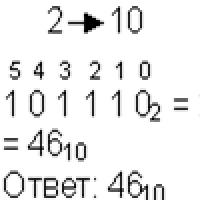 Liten matematisk fakultet
Liten matematisk fakultet "Varför drömmer du om en runddans i en dröm?
"Varför drömmer du om en runddans i en dröm? Varför drömmer du om kyrkan inuti: tolkning av drömmens betydelse enligt olika drömböcker för män och kvinnor
Varför drömmer du om kyrkan inuti: tolkning av drömmens betydelse enligt olika drömböcker för män och kvinnor Drömtolkning av persimmon, varför drömmer du om persimmon i en dröm för att se persimmon i en dröm varför
Drömtolkning av persimmon, varför drömmer du om persimmon i en dröm för att se persimmon i en dröm varför Förtrollad själ Betydelsen av karmiska tal
Förtrollad själ Betydelsen av karmiska tal