Vilka är nummersystemen? Liten matematisk fakultet. Konvertera bråkdelen av decimalsystemet till något annat
Notationär en metod för att skriva ett nummer med en angiven uppsättning specialtecken (siffror).
Notering:
- ger en representation av en uppsättning tal (heltal och/eller reella);
- ger varje nummer en unik representation (eller åtminstone en standardrepresentation);
- visar den algebraiska och aritmetiska strukturen för ett tal.
Att skriva ett nummer i något talsystem kallas nummerkod.
En separat position i en nummervisning anropas ansvarsfrihet, vilket betyder att positionsnumret är rangnummer.
Antalet siffror i ett nummer kallas bitdjup och sammanfaller med dess längd.
Nummersystem är indelade i positionella Och icke-positionell. Positionsnummersystem är uppdelade
på homogen Och blandad.
oktalt talsystem, hexadecimalt talsystem och andra talsystem.
Översättning av nummersystem. Tal kan konverteras från ett talsystem till ett annat.
Tabell över överensstämmelse mellan siffror i olika nummersystem.
Det finns positionella och icke-positionella nummersystem.
I icke-positionella nummersystem vikten av en siffra (dvs det bidrag den ger till värdet på siffran) beror inte på hennes position att skriva numret. Således, i det romerska talsystemet i talet XXXII (trettiotvå), är vikten av talet X i valfri position helt enkelt tio.
I positionsnummersystem vikten av varje siffra varierar beroende på dess position (position) i siffrorna som representerar numret. Till exempel, i talet 757,7 betyder de första sju 7 hundra, den andra - 7 enheter och den tredje - 7 tiondelar av en enhet.
Själva notationen av talet 757,7 betyder en förkortad notation av uttrycket
700 + 50 + 7 + 0,7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757,7.
Varje positionsnummersystem kännetecknas av sitt grund.
Alla naturliga tal kan tas som basen i systemet - två, tre, fyra, etc. Därav, otaliga positionssystem möjliga: binär, ternär, kvartär, etc. Skriva tal i varje talsystem med en bas q betyder ett stenografiuttryck
a n-1 q n-1 +a n-2 q n-2 + ... +a 1 q 1 +a 0 q 0 +a -1 q -1 + ... +a -m q -m ,
Var a i - nummer i nummersystemet; n Och m - antalet heltals respektive bråksiffror. Till exempel:
Vilka nummersystem använder specialister för att kommunicera med en dator?
Förutom decimal används i stor utsträckning system med en bas som är en heltalspotens på 2, nämligen:
binär(siffrorna 0, 1 används);
oktal(siffrorna 0, 1, ..., 7 används);
hexadecimal(för de första heltal från noll till nio används siffrorna 0, 1, ..., 9, och för nästa siffror - från tio till femton - används symbolerna A, B, C, D, E, F som siffror).
Det är användbart att komma ihåg notationen i dessa talsystem för de två första tiotals heltal:
|
|
|
Av alla nummersystem särskilt enkelt och därför Det binära talsystemet är intressant för teknisk implementering i datorer.
Vad är ett talsystem?
Vad är ett talsystem? Ett talsystem är en uppsättning tekniker och regler genom vilka siffror skrivs och läses.
Det finns positionella och icke-positionella nummersystem.
I icke-positionella talsystem är vikten av en siffra (det vill säga bidraget den ger till värdet av talet) inte beroende av dess position i talets notation. Således, i det romerska talsystemet i talet XXXII (trettiotvå), är vikten av talet X i valfri position helt enkelt tio.
I positionsnummersystem varierar vikten av varje siffra beroende på dess position (position) i siffersekvensen som representerar numret. Till exempel, i talet 757,7 betyder de första sju 7 hundra, den andra - 7 enheter och den tredje - 7 tiondelar av en enhet.
Själva notationen av numret 757.7 betyder en förkortad notation av uttrycket:
Varje positionstalsystem kännetecknas av sin bas.
Basen i ett positionsnummersystem är antalet olika siffror som används för att representera tal i ett givet talsystem.
Alla naturliga tal kan tas som basen i systemet - två, tre, fyra, etc. Följaktligen är ett oändligt antal positionssystem möjliga: binära, ternära, kvartära, etc.
Hur genereras heltal i positionstalssystem?
I varje talsystem är siffror ordnade efter deras betydelser: 1 är större än 0, 2 är större än 1, etc.
Att främja en siffra avser att ersätta den med den näst högsta.
Att flytta fram siffran 1 betyder att ersätta den med 2, att flytta fram siffran 2 innebär att ersätta den med 3 osv. Att främja en ledande siffra (till exempel siffran 9 i decimalsystemet) innebär att man ersätter den med en 0. I ett binärt system, som bara använder två siffror - 0 och 1, innebär att främja en 0 att man ersätter den med en 1 och främjar en 1 betyder att ersätta den med en 0.
För att bilda ett heltal efter ett givet heltal måste siffran längst till höger i talet flyttas fram; om något nummer blir noll efter befordran, måste du flytta fram numret till vänster om det.
Genom att tillämpa denna regel skriver vi ner de första tio heltal
· i binärt system: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
· i det ternära systemet: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
· i det femfaldiga systemet: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
· i oktalt system: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Förutom decimal används i stor utsträckning system med en bas som är en heltalspotens på 2, nämligen:
| Binärt system | Kvartärt system | Oktalt system | Decimalsystem | Hexadecimalt system |
| 1 | 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 | 3 |
| 100 | 10 | 4 | 4 | 4 |
| 101 | 11 | 5 | 5 | 5 |
| 110 | 12 | 6 | 6 | 6 |
| 111 | 13 | 7 | 7 | 7 |
| 1000 | 20 | 10 | 8 | 8 |
| 1001 | 21 | 11 | 9 | 9 |
| 1010 | 22 | 12 | 10 | A |
| 1011 | 23 | 13 | 11 | B |
| 1100 | 30 | 14 | 12 | C |
| 1101 | 31 | 15 | 13 | D |
| 1110 | 32 | 16 | 14 | E |
| 1111 | 33 | 17 | 15 | F |
| 10000 | 40 | 20 | 16 | 10 |
Människor föredrar decimalsystemet förmodligen för att de har räknat på sina fingrar sedan urminnes tider, och människor har tio fingrar och tår. Människor använder inte alltid och inte överallt decimaltalssystemet. I Kina använde man till exempel det femsiffriga nummersystemet under lång tid.
Och datorer använder det binära systemet eftersom det har ett antal fördelar jämfört med andra system:
· för att implementera det behöver vi tekniska enheter med två stabila tillstånd (det finns ström - ingen ström, magnetiserad - inte magnetiserad, etc.), och inte till exempel med tio, som i decimal;
· presentation av information genom endast två tillstånd är tillförlitlig och bullerbeständig;
· det är möjligt att använda apparaten för boolesk algebra för att utföra logiska transformationer av information;
· Binär aritmetik är mycket enklare än decimalräkning.
Nackdelen med det binära systemet är den snabba ökningen av antalet siffror som krävs för att registrera nummer.
Varför använder datorer också oktala och hexadecimala talsystem?
Det binära systemet, bekvämt för datorer, är obekvämt för människor på grund av dess skrymmande och ovanliga notation.
Omvandlingen av tal från decimalsystemet till det binära systemet och vice versa utförs av en maskin. Men för att använda en dator professionellt måste du lära dig att förstå ordet maskin. Det är därför de oktala och hexadecimala systemen utvecklades.
Siffror i dessa system är nästan lika lätta att läsa som decimala; de kräver tre (oktala) respektive fyra (hexadecimala) gånger färre siffror än i det binära systemet (trots allt är talen 8 och 16 respektive tredje och fjärde potensen av talet 2) .
Konvertera tal från ett talsystem till ett annat
Numret p av olika siffror som används i positionssystemet bestämmer namnet på nummersystemet och kallas basen för nummersystemet - "p". Valfritt tal N i positionstalssystemet med bas p kan representeras som ett polynom i bas p:
N = a n p n +a n-1 p n-1 + ... +a 1 p+a 0 +a -1 p -1 +a -2 p -2 + ... (1.1)
här är N ett tal, a j är koefficienter (siffror i ett tal), p är basen i talsystemet (p>1). Det är vanligt att representera siffror som en sekvens av siffror:
N = a n a n -1 ... a 1 a 0 . a -1 a -2 ...
Omvandlingen av tal till decimalsystemet görs genom att man sammanställer en potensserie med basen av systemet (se formel 1.1) från vilket talet översätts. Värdet av summan beräknas sedan.
|
|
|
|
Omvandlingen av heltal decimala tal till ett icke-decimalt talsystem utförs genom att sekventiellt dividera decimaltalet med basen av systemet till vilket det omvandlas tills kvoten av denna bas erhålls. Numret i det nya systemet skrivs som divisionsrester, med början från det sista.
Exempel: Låt oss konvertera talet 75 från decimal till binär, oktal och hexadecimal:

Svar: 75 10 = 1 001 011 2 = 113 8 = 4B 16.
Konvertera korrekta bråk från det decimala talsystemet till det icke-decimala talsystemet. För att konvertera ett regelbundet decimalbråk till ett annat system, måste detta bråktal multipliceras sekventiellt med basen för det system till vilket det konverteras. I detta fall multipliceras endast bråkdelar. Bråk i det nya systemet skrivs i form av hela delar av produkter, med början från den första.
Exempel. Låt oss konvertera talet 0,36 från decimalsystemet till binärt, oktalt och hexadecimalt:

För att konvertera ett oregelbundet decimalbråk till ett talsystem med en icke-decimalbas måste du konvertera hela delen och bråkdelen separat. Översätt 23.125 10 2 s.s.
Talsystem kallas multipel om följande relation gäller: S = R N , där S, R är talsystemens baser, N är graden av multiplicitet (heltal: 2, 3 ...).
För att konvertera ett tal från talsystemet R till dess multipla talsystem S, fortsätt enligt följande: flyttar du från punkten till vänster och höger delar de upp talet i grupper med N siffror, och kompletterar grupperna längst till vänster och längst till höger med nollor, om nödvändig. Gruppen ersätts då av motsvarande siffra från S-nummersystemet.
| Översätt 1101111001.1101 2 "8" s.s. | Översätt 11111111011.100111 2 "16" s.c. |
För att konvertera ett tal från talsystemet S till dess multipla talsystem R räcker det att ersätta varje siffra i detta nummer med motsvarande nummer från talsystemet R, medan obetydliga nollor i hög (00512) och låg (15,124000) siffror kasseras.
| Översätt 305.4 8 "2" s.s. | Översätt 7B2.E 16 "2" s.s. |
|
|
Om du behöver konvertera från ett talsystem S till R, förutsatt att de inte är multiplar, måste du försöka välja ett talsystem K så att: S = K N och R = K N .
Översätt 175.24 8 "16" s.s.
Resultat: 175.24 8 = 7D.5 16.
Om talsystemet K inte kan hittas, bör översättningen utföras med hjälp av decimaltalssystemet som mellanliggande.
Exempel på allt detta
Att konvertera oktala och hexadecimala tal till det binära systemet är mycket enkelt: det räcker att ersätta varje siffra med dess ekvivalenta binära triad (tre siffror) eller tetrad (fyra siffror).
Till exempel:
För att konvertera ett tal från binärt till oktalt eller hexadecimalt måste du dela upp det till vänster och höger om decimalkomma i triader (för oktala) eller tetrader (för hexadecimala) och ersätta varje sådan grupp med motsvarande oktala (hexadecimala) siffra . Till exempel:

Addition i olika nummersystem
Tilläggstabeller är lätta att skapa med hjälp av räkneregeln.






Subtraktion i olika talsystem

Multiplikation i olika talsystem
När man multiplicerar flersiffriga tal i olika positionstalssystem kan man använda den vanliga algoritmen för att multiplicera tal i en kolumn, men resultatet av multiplicering och addering av ensiffriga tal måste lånas från multiplikations- och additionstabellerna som motsvarar systemet i fråga.



Indelning i olika talsystem
Division i valfritt positionstalssystem utförs enligt samma regler som division med vinkel i decimalsystemet. I det binära systemet är division särskilt enkelt, eftersom nästa siffra i kvoten bara kan vara noll eller en.
Multiplicera med basen av det nya talsystemet tills det nya bråket innehåller det erforderliga antalet siffror, vilket bestäms av den erforderliga noggrannheten i representationen av bråket. Ett korrekt bråk i det nya talsystemet skrivs från heltalsdelar av produkter som är resultatet av sekventiell multiplikation, och den första heltalsdelen kommer att vara den högsta siffran i det nya bråket. Låt oss ta ett exempel...

Representationerna i dem är ganska stora siffror, eftersom detta resulterar i en extremt besvärlig notering av siffror eller kräver ett mycket stort alfabet av siffror som används. Datorer använder endast positionsnummersystem, där den kvantitativa motsvarigheten till varje siffra i alfabetet beror inte bara på typen av denna siffra, utan också på dess placering i numrets notation. Positionsnummersystem...





Sekvenserna 0 och 1. Till exempel kommer ett icke-negativt heltal A2=T 111100002 att lagras i en cell enligt följande: 1 1 1 1 0 0 0 0 Det betyder att vi kan skriva alla tal från 0 till 255 i binären nummersystem i 1 minnescell. 2.2 Representation av tal i en dator Heltal i en dator lagras i minnesceller, i detta fall motsvarar varje siffra i en minnescell...
Representerar siffror med hjälp av skrivna symboler.
Notering:
- ger representationer av en uppsättning tal (heltal och/eller reella);
- ger varje nummer en unik representation (eller åtminstone en standardrepresentation);
- återspeglar den algebraiska och aritmetiska strukturen hos tal.
Nummersystem är indelade i positionella, icke-positionell Och blandad.
Positionsnummersystem
I positionsnummersystem har samma siffertecken (siffra) i beteckningen för ett tal olika betydelser beroende på platsen (siffran) där det finns. Uppfinningen av positionsnumrering, baserad på platsbetydelsen av siffror, tillskrivs sumererna och babylonierna; Sådan numrering utvecklades av hinduerna och fick ovärderliga konsekvenser i den mänskliga civilisationens historia. Sådana system inkluderar det moderna decimaltalssystemet, vars uppkomst är förknippad med att räkna på fingrar. Den dök upp i det medeltida Europa genom italienska köpmän, som i sin tur lånade den av muslimer.
Positionsnummersystemet hänvisar vanligtvis till det -rika talsystemet, som bestäms av ett heltal som anropas grund nummersystem. Ett heltal utan tecken i det -ary talsystemet representeras som en finit linjär kombination av potenser av ett tal:
, där kallas heltal i antal, som tillfredsställer ojämlikheten.Varje grad i en sådan notation kallas en rangvikt. Ancienniteten för siffrorna och deras motsvarande siffror bestäms av värdet på indikatorn (siffernummer). Vanligtvis utelämnas de vänstra nollorna i tal som inte är noll.
Om det inte finns några avvikelser (till exempel när alla siffror presenteras i form av unika skrivna tecken), skrivs numret som en sekvens av dess alfanumeriska siffror, listade i fallande ordningsföljd av siffror från vänster till höger:
Till exempel nummer etthundratre representeras i decimaltalssystemet som:
De mest använda positionssystemen är:
I positionssystem gäller att ju större basen av systemet är, desto färre antal siffror (det vill säga skrivna siffror) krävs när man skriver ett nummer.
Blandade talsystem
Blandat nummersystemär en generalisering av det -rika talsystemet och syftar också ofta på positionstalssystem. Grunden för det blandade talsystemet är en ökande sekvens av tal, och varje nummer i det representeras som en linjär kombination:
, där koefficienterna kallas som tidigare i antal, vissa begränsningar gäller.Att skriva ett tal i ett blandat talsystem är listningen av dess siffror i fallande indexordning, med början med den första som inte är noll.
Beroende på typen som funktion av, kan blandade talsystem vara potens, exponentiella, etc. När för vissa sammanfaller det blandade talsystemet med det exponentiella -rika talsystemet.
Det mest kända exemplet på ett blandat talsystem är representationen av tid som antal dagar, timmar, minuter och sekunder. I det här fallet motsvarar värdet på "dagar, timmar, minuter, sekunder" värdet på sekunder.
Faktoriellt nummersystem
I fakultativt talsystem baserna är en sekvens av faktorialer, och varje naturligt tal representeras som:
, Var .Faktorialnummersystemet används när avkodning av permutationer genom listor med inversioner: med numret på permutationen kan du reproducera det på följande sätt: ett tal som är ett mindre än talet (numreringen börjar från noll) skrivs i faktorialsystemet, och koefficienten för talet i! kommer att beteckna antalet inversioner för element i+1 i uppsättningen där permutationerna görs (antalet element mindre än i+1, men placerade till höger om det i den önskade permutationen)
Exempel: överväg en uppsättning permutationer av 5 element, det finns 5 totalt! = 120 (från permutationsnummer 0 - (1,2,3,4,5) till permutationsnummer 119 - (5,4,3,2,1)), låt oss hitta den 101:a permutationen: 100 = 4!* 4 + 3!*0 + 2!*2 + 1!*0 = 96 + 4; låt ti vara koefficienten för talet i!, då är t4 = 4, t3 = 0, t2 = 2, t1 = 0, då: antalet element mindre än 5, men placerade till höger är 4; antalet element mindre än 4, men placerade till höger är 0; antalet element mindre än 3, men placerade till höger är 2; antalet element mindre än 2, men placerade till höger är 0 (det sista elementet i permutationen "läggs" på den enda kvarvarande platsen) - alltså kommer den 101:a permutationen att se ut så här: (5,3,1,2 ,4) Kontroll av denna metod kan utföras genom att direkt räkna inversionerna för varje element i permutationen.
Fibonaccis talsystem baserat på Fibonacci-tal. Varje naturligt tal representeras i formen:
, där finns Fibonacci-talen, och koefficienterna har ett ändligt antal ettor och det finns inga två ettor i rad.Icke-positionella nummersystem
I icke-positionella talsystem beror värdet som en siffra anger inte på dess position i talet. I det här fallet kan systemet införa begränsningar på positionen för siffrorna, till exempel, så att de är ordnade i fallande ordning.
Binomialt talsystem
Representation med hjälp av binomialkoefficienter
, Var .Residual Class System (RSS)
Representationen av tal i restklasssystemet baseras på begreppet rest och den kinesiska restsatsen. RNS bestäms av en uppsättning av relativt prime moduler med produkten på ett sådant sätt att varje heltal från segmentet är associerat med en uppsättning rester, där
…Samtidigt garanterar den kinesiska restsatsen det unika i representationen för tal från intervallet.
I RNS utförs aritmetiska operationer (addition, subtraktion, multiplikation, division) komponentvis om resultatet är känt för att vara ett heltal och även ligger i .
Nackdelarna med RNS är möjligheten att endast representera ett begränsat antal nummer, samt avsaknaden av effektiva algoritmer för att jämföra de nummer som representeras i RNS. Jämförelse utförs vanligtvis genom översättning av argument från RNS till ett blandat radixtalsystem.
Stern–Brocot nummersystem- ett sätt att skriva positiva rationella tal, baserat på Stern–Brocot-trädet.
Nummersystem för olika nationer
Enhetsnummersystem
Tydligen kronologiskt det första siffersystemet för varje nation som behärskar räkning. Ett naturligt tal representeras genom att samma tecken upprepas (streck eller punkt). Till exempel, för att avbilda numret 26, måste du rita 26 linjer (eller göra 26 skåror på ett ben, en sten, etc.). Därefter, för bekvämlighetens skull för att uppfatta stora antal, grupperas dessa tecken i grupper om tre eller fem. Sedan börjar lika volymgrupper av tecken ersättas av något nytt tecken - så här uppstår prototyper av framtida siffror.
Forntida egyptiska talsystem
Babyloniska talsystemet
Alfabetiska talsystem
Alfabetiska nummersystem användes av de gamla armenierna, georgierna, greker (joniskt talsystem), araber (abjadia), judar (se gematria) och andra folk i Mellanöstern. I slaviska liturgiska böcker översattes det grekiska alfabetiska systemet till kyrilliska bokstäver.
judiskt nummersystem
Grekiskt nummersystem
Romerskt talsystem
Det kanoniska exemplet på ett nästan icke-positionellt talsystem är det romerska, som använder latinska bokstäver som siffror:
Jag står för 1,
V - 5,
X - 10,
L - 50,
C - 100,
D - 500,
M - 1000
Till exempel, II = 1 + 1 = 2
här står symbolen I för 1 oavsett dess plats i talet.
Faktum är att det romerska systemet inte är helt icke-positionellt, eftersom den mindre siffran som kommer före den större subtraheras från den, till exempel:
IV = 4, medan:
VI = 6
Mayan nummersystem
se även
Anteckningar
Länkar
- Gashkov S.B. Nummersystem och deras tillämpningar. - M.: MTsNMO, 2004. - (Biblioteket "Mathematical Education").
- Fomin S.V. Nummersystem. - M.: Nauka, 1987. - 48 sid. - (Populära föreläsningar om matematik).
- Yaglom I. Nummersystem // Kvant. - 1970. - Nr 6. - S. 2-10.
- Siffror och talsystem. Online Encyclopedia Around the World.
- Stakhov A. Talsystemens roll i datorernas historia.
- Mikushin A.V. Nummersystem. Föreläsningskurs "Digitala enheter och mikroprocessorer"
- Butler J. T., Sasao T. Redundanta talsystem med flera värden Artikeln diskuterar talsystem som använder siffror större än en och tillåter redundans i representationen av tal
Wikimedia Foundation. 2010.
oxar (kategorier). Detta tillvägagångssätt används vid överföring, lagring och bearbetning av information och är vanligtvis inte associerat med informationens semantiska innehåll.
1.5.2. Probabilistiskt synsätt
I informationsteori definieras information som borttagen osäkerhet. Detta tar hänsyn till informationens värde för mottagaren. Informationsmängden bestäms av hur mycket osäkerhetsmåttet (entropi) minskar efter att man tagit emot ett meddelande eller inträffat av en händelse.
En enhet för informationskvantitet (bit) anses vara mängden information som innehåller ett meddelande som minskar informationsosäkerheten med 2 gånger. I allmänhet bestäms mängden information (H) i ett meddelande om att en av N lika sannolika händelser har inträffat enligt följande:
En grupp på 8 bitar kallas en byte. Om en bit är den minsta informationsenheten, är en byte den viktigaste. Det finns härledda informationsenheter:
1 byte = 8 bitar;
1 kilobyte = 210 byte = 1024 byte;
1 megabyte = 220 byte = 1024 kilobyte;
1 Gigabyte = 230 byte = 1024 Megabyte;
1 Terabyte = 240 byte = 1024 Gigabyte.
1.6. Nummersystem som används inom datavetenskap
Ett talsystem är en uppsättning tekniker och regler för att skriva tal med siffror. Det finns icke-positionella och positionella nummersystem.
I I ett icke-positionellt talsystem har varje symbol sin egen specifika betydelse, som inte beror på symbolens position i nummerposten. Till exempel i det romerska talsystemet
I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000. Siffran 77 skrivs LXXVII.
I I ett positionsnummersystem beror värdet på valfri siffra i bilden av ett tal på dess position (position) i sifferserien som representerar det givna talet. Till exempel: 77 - 7 enheter och 7 tior.
Varje positionsnummersystem har ett strikt definierat antal symboler (siffror) för att representera vilket nummer som helst:
– binär - 2: 0 och 1;
– decimal - 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Antalet siffror som används i positionsnummersystemet för att skriva tal kallas basen i talsystemet. Talsystemets bas kan vara vilket naturligt tal som helst.
Låt q vara basen i systemet, då kan vilket tal som helst i talsystemet med basen q representeras som:
A q = a n q n + a n –1 q n –1 + ... + a 1 q 1 + a 0 q 0 + a –1 q –1 + a –2 q –2 + ... + a –k q–k , (3) där A q är ett tal skrivet i ett talsystem med basen q,
n + 1 - antalet siffror i talets heltalsdel,
och i är siffrorna i numret, med 0 ≤ a i< q ,
k - antalet siffror i bråkdelen av talet.
Inom datavetenskap används endast positionsnummersystem: decimal, binär, oktal, hexadecimal.
1.6.1. Regler för omvandling av tal från ett talsystem till ett annat
Regel 1. För att konvertera ett heltals decimaltal A till ett talsystem med basen q, är det nödvändigt att dividera talet A med basen q tills en hel återstod erhålls som är mindre än q. Den resulterande kvoten ska delas igen med q tills en hel rest mindre än q erhålls, etc. tills den sista kvoten är mindre än q. Sedan ska decimaltalet A i talsystemet med basen q skrivas som en sekvens av divisionsrester i omvänd ordning mot kvittot, där den högsta siffran ger den sista kvoten.
Regel 2. För att konvertera ett decimaltal till ett talsystem med basen q, multiplicera detta tal med basen q. Heltalsdelen av produkten kommer att vara den första siffran i ett tal i talsystemet med basen q. Ta sedan bort hela delen, multiplicera igen med basen q osv. tills det erforderliga antalet siffror i det nya nummersystemet erhålls eller tills översättningen är klar.
Regel 3. Blandade tal i decimaltalssystemet översätts i två steg: separat heltalsdelen enligt sin egen regel och separat bråkdelen enligt sin egen regel. Sedan skrivs det totala resultatet ner, vars bråkdel separeras med kommatecken.
Regel 4. För att konvertera ett tal från ett talsystem med basen q till ett decimaltalssystem bör du använda formen för att skriva talet i formen (3).
Regel 5. För att konvertera ett heltal från det binära talsystemet till det oktala systemet behöver du en sekvens av binära siffror av olika storlek.




 Berättelsen om piloterna som bombade Hiroshima och Nagasaki
Berättelsen om piloterna som bombade Hiroshima och Nagasaki Smidig kapacitetsladdning: vad ska man välja?
Smidig kapacitetsladdning: vad ska man välja?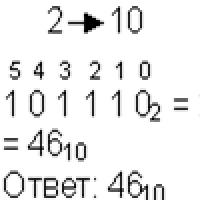 Liten matematisk fakultet
Liten matematisk fakultet "Varför drömmer du om en runddans i en dröm?
"Varför drömmer du om en runddans i en dröm? Varför drömmer du om kyrkan inuti: tolkning av drömmens betydelse enligt olika drömböcker för män och kvinnor
Varför drömmer du om kyrkan inuti: tolkning av drömmens betydelse enligt olika drömböcker för män och kvinnor Drömtolkning av persimmon, varför drömmer du om persimmon i en dröm för att se persimmon i en dröm varför
Drömtolkning av persimmon, varför drömmer du om persimmon i en dröm för att se persimmon i en dröm varför Förtrollad själ Betydelsen av karmiska tal
Förtrollad själ Betydelsen av karmiska tal