Точні методи дослідження нелінійних сау. Методи дослідження нелінійних систем Методи аналізу нелінійних автоматичних систем
Спільним способом дослідження стійкості нелінійних систем є прямий спосіб Ляпунова. У його основі лежить теорема Ляпунова про стійкість нелінійних систем. Як апарат дослідження використовується так звана функція Ляпунова, що є знако-визначеною функцією координат системи, що має також знако-визначену похідну за часом. Застосування цього обмежується його складністю.
Простішим методом розрахунку стійкості нелінійних систем є метод, розроблений румунським ученим В. М. Поповим. Однак він придатний для деяких окремих випадків.
Процеси в нелінійній системі можуть бути досліджені на основі шматково-лінійної апроксимації. У цьому випадку нелінійні характеристики окремих ланок розбивають на ряд лінійних ділянок, у межах яких завдання виявляється лінійним і може бути вирішено досить просто. На межах ділянок необхідно провести «зшивання» окремих шматків процесу єдиний процес. Метод може застосовуватися, якщо кількість ділянок, куди розбивається нелінійна характеристика, невелика. Це, наприклад, місце для релейних характеристик (див. рис. 5.1). При великому числі ділянок метод виявляється занадто громіздким. Однак використання ЕОМ дозволяє подолати цю труднощі та з успіхом розраховувати процеси в нелінійних системах за будь-яких нелінійних характеристик і взагалі за наявності нелінійних залежностей довільного вигляду.
p align="justify"> Метод фазового простору в принципі дозволяє досліджувати системи з нелінійностями довільного вигляду, а також з декількома іелінійностями. При цьому у фазовому просторі будують так званий фазовий портрет процесів, що протікають (у нелінійній системі. По виду фазового портрета можна судити про стійкість, можливість виникнення автоколивань, точності в режимі, що встановився. Однак розмірність фазового простору дорівнює порядку диференціального рівняння нелінійної системи. методу дослідження систем, що описуються диференціальним рівнянням вище другого порядку.У разі диференціального рівняння другого порядку фазовий простір являє собою фазову площину, і цей метод може бути з успіхом застосований .
Для аналізу випадкових процесів у нелінійних автоматичних системах можна застосовувати математичний апарат теорії випадкових марківських процесів. Однак складність методу та можливість
Рішення рівняння Фоккера - Планка, яка потрібна при аналізі, тільки для рівнянь першого і деяких випадках другого порядку, обмежує його використання.
Усі перелічені методи належать до точних. Їх складність і обмеженість застосування сприяли розробці наближених, але простіших методів дослідження нелінійних систем. Наближені методи дозволяють у багатьох випадках досить просто отримати прозорі та легко доступні для огляду результати аналізу нелінійних систем . Фазові траєкторії на ділянці< x < a представляют собой прямые с коэффициентом наклона -1/Т 1 при различных значениях начальных условий.
На прямих лініях проставляємо стрілки таким чином, щоб кінцевий рух прагнув початку координат.
Нехайх > a, ![]() . При цьому вихідна система нелінійних рівнянь має вигляд
. При цьому вихідна система нелінійних рівнянь має вигляд
 (27)
(27)
де c i - сімейство ізоклін, що є прямі паралельні осі х, тобто. , де визначається з виразу для
 . (28)
. (28)
Таким чином
 . (29)
. (29)
Задаючись значеннями, будуємо сімейство ізоклін. Визначаємо кути перетину ізоклін фазовими траєкторіями.
Так як ![]() . Наприклад, якщо a = 90°.
. Наприклад, якщо a = 90°.
Нехайх< – a, ![]() . Побудову виконуємо аналогічно, оскільки знак змінився, то будуть інші кути перетинів ізоклін фазовою траєкторією. Фазовий портрет системи наведено на рис. 15.
. Побудову виконуємо аналогічно, оскільки знак змінився, то будуть інші кути перетинів ізоклін фазовою траєкторією. Фазовий портрет системи наведено на рис. 15.
 |
 |
Мал. 14 Мал. 15
Знімемо спрощенняДо = 0, тобто. розглянемо вплив негативного зворотний зв'язок швидкості двигуна на характер фазової траєкторії.
При цьому рівняння мають вигляд:
 (30)
(30)
Нехай ![]() , при цьому перемикання відбуватиметься за умови
, при цьому перемикання відбуватиметься за умови ![]() (а не умови х = а), це рівняння лінії (рис. 16)
(а не умови х = а), це рівняння лінії (рис. 16)
У цьому кількість перерегулювань зменшується; можна підібрати такий нахил, при якому немає перехитування.
Розглянемо фазовий портрет без обмежень.У системі без обмежень фазовий портрет можна подати на трилистої поверхні з похилими гранями (рис. 17.) При цьому лист 2 відповідає зоні нечутливості z = 0, лист 1 відповідає негативним значенням z, а лист 3 позитивним. Внаслідок гістерези має місце часткове накладення листів.

Мал. 16 Мал. 17
Досліджуємо систему. Досліджуємо вплив негативного зворотного зв'язку за швидкістю двигуна (тобто вплив величини – К). Нехай значення До збільшується, при цьому нахил прямих зменшується, і може вийти, що зріз буде пологішим ніж нахил характеристики в середній частині. Це призводить до частих перемикань. Такий режим називається ковзним. Якщо зона дуже вузька, то рух як би зісковзує до режиму, що встановився (рис. 18а).
Якщо змінити знак зворотного зв'язку з негативного зв'язку на позитивний зв'язок, то при цьому зміниться нахил ліній перемикання, і кількість коливань збільшуватиметься, система "розгойдуватиметься". Система працює, як генератор і може з'явитися або замкнутий цикл - автоколивання, або перехідний процес, що розходиться (рис. 18б).

Переваги методу:простота та наочність для систем 2-го порядку; придатність до будь-якого типу нелінійних елементів.
Недоліки:метод громіздкий для систем вище 2-го порядку, тому за n >2 не застосовується.
Розглянемо кілька прикладів побудови фазових портретів нелінійних систем управління
приклад 1.Нехай задана система, що складається з лінійної частини та нелінійного елемента (підсилювач з обмеженням по модулю) (рис. 19). Це кусочно-линейная система, оскільки у окремих ділянках вона поводиться як лінійна (в області) – а, +а[). Допустимо в області (] - а, + а [) коефіцієнт посилення великий і система нестійка а фазовий портрет характеризується особливою точкою "нестійкий фокус". За межами області коефіцієнт посилення малий, припустимо, що у своїй система стійка і характеризується особливої точкою – " стійкий фокус " .
За великих відхилень x > |a| загальний коефіцієнт посилення системи малий, система стійка, процес загасає.
При малих відхиленнях загальний коефіцієнт посилення системи великий – процес розходиться до замкнутої траєкторії, що характеризує наявність стійких автоколивань (рис. 20).
У цій системі три типи рухів: автоколивання; схожі коливання; коливання, що розходяться

приклад 2.Нехай задана система з характеристикою нелінійної ланки типу "зона нечутливості" (рис. 21). Необхідно збудувати фазовий
портрет даної системи, визначити наявність граничних циклів та проаналізувати їх стійкість.
Побудуємо фазовий портрет
1) При - a< x < +a f(x) = 0, а система уравнений имеет вид

 |
Фазовий портрет у цій галузі є сімейством прямих з коефіцієнтом до = -1, а стан рівноваги стійкий за Ляпуновим і представляє відрізок осі y = 0 на інтервалі – a 2) При x > +a f(x) = x – a, а система рівнянь має вигляд 3) При x< – a f(x) = x + a, а система уравнений имеет вид Вихідну схему можна у вигляді (рис. 27). Побудуємо фазовий портрет. 1) При -1< x < +1 f(x) = x, а система уравнений имеет вид Для кожного з i визначимокутовий коефіцієнт нахилу ізокліни – до за формулою 2) При x > +1 f(x) = 1, а система рівнянь має вигляд Для кожного з i визначимокутовий коефіцієнт нахилу ізокліни – до за формулою 3) При x< -1 f(x) = -1. Ліва частина фазового портрета будується аналогічно правої. Література 1. Атабеков Г.І., Тимофєєв А.Б., Купалян С.Д., Хухріков С.С. Теоретичні засади електротехніки (ТОЕ). Нелінійні електричні кола. Електромагнітне поле. 5-те вид. Вид-во: ЛАНЬ, 2005. - 432 с. 2. Гаврилов Нелінійні ланцюги у програмах схемотехнічного моделювання. Вид-во: СОЛОН-ПРЕС, 2002. - 368 с. 3. Дорф Р., Бішоп Р. Автоматика. Сучасні системи керування. 2002 р. - 832 с. 4. Теорія автоматичного керування. Навч. для вузів за спец. "Автоматика та телемеханіка". У 2-х год./Н.А. Бабаков, А.А. Воронов та інших.: Під ред. А.А. Воронова. - 2-ге вид., перероб. та дод. - М.: Вищ. шк., 1986. - 367 с., Іл. 5. Харазов В.Г. Інтегровані системи керування технологічними процесами: Довідник. Видавництво: ПРОФЕСІЯ, ВИДАВНИЦТВО, 2009. - 550 с. Предмет: "Теорія автоматичного керування" Тема: "Методи дослідження нелінійних систем" 1. Метод диференціальних рівнянь Диференціальне рівняння замкнутої нелінійної системи n-го порядку (рис. 1) можна перетворити на систему n-диференціальних рівнянь першого порядку як: де: - Змінні, що характеризують поведінку системи (одна з них може бути регульована величина); - Нелінійні функції; u - вплив, що задає. Зазвичай ці рівняння записуються в кінцевих різницях: де – Початкові умови. Якщо відхилення 2. Метод фазового простору Розглянемо випадок, коли зовнішній вплив дорівнює нулю (U = 0). Рух системи визначається зміною її координат - Фазовим просторомназивається простір координат системи. Зі зміною часу t точка М рухається по траєкторії, яка називається фазовою траєкторією. Якщо змінювати початкові умови отримаємо сімейство фазових траєкторій, які називаються фазовим портретом. Фазовий портрет визначає характер перехідного процесу у нелінійній системі. Фазовий портрет має особливі точки, яких прагнуть чи яких йдуть фазові траєкторії системи (їх може бути кілька). Фазовий портрет може містити замкнуті фазові траєкторії, які називаються граничними циклами.Граничні цикли характеризують автоколивання у системі. Фазові траєкторії ніде не перетинаються, крім спеціальних точок, що характеризують рівноважні стани системи. Граничні цикли та стану рівноваги можуть бути стійкими або нестійкими. Фазовий портрет повністю характеризує нелінійну систему. Характерною особливістю нелінійних систем є наявність різних типів рухів, кількох станів рівноваги, граничних циклів. p align="justify"> Метод фазового простору є фундаментальним методом дослідження нелінійних систем. Дослідити нелінійних систем на фазовій площині набагато простіше та зручніше, ніж за допомогою побудови графіків перехідних процесів у часовій області. Геометричні побудови у просторі менш наочні, ніж побудови на площині, коли система має другий порядок, при цьому застосовується метод фазової площини. Застосування методу фазової площини для лінійних систем Проаналізуємо зв'язок між характером перехідного процесу та кривими фазових траєкторій. Фазові траєкторії можуть бути отримані шляхом інтегрування рівняння фазової траєкторії, або шляхом вирішення вихідного диференціального рівняння 2-го порядку. Нехай задано систему (рис. 3). Розглянемо вільний рух системи. При цьому: U(t) = 0, e (t) = - x (t) У загальному вигляді диференціальне рівняння має вигляд Це однорідне диференціальне рівняння 2-го порядку його характеристичне рівняння одно Коріння характеристичного рівняння визначається із співвідношень Представимо диференціальне рівняння 2-го порядку як системи рівнянь 1-го порядку: У лінійній системі, що розглядається, змінні x і y являють собою фазові координати. Фазовий портрет будуємо у просторі координат x і y, тобто. на фазовій площині. Якщо виключимо час із рівняння (1), то отримаємо рівняння інтегральних кривих чи фазових траєкторій. Це рівняння з змінними, що розділяються 1. Нехай коріння характеристичного рівняння (3) має вигляд При цьому перехідний процес описується рівняннями x = A (wt+j), (8) y = Aw cos (wt+j), тобто. є незагасаючими коливаннями з постійною амплітудою А і початковою фазою – j. На фазовій площині (рис. 4) ці рівняння є параметричними рівняннями еліпса з півосями А і wA (де A – постійна інтегрування). Якщо позначити Рівняння еліпса можна отримати рішенням рівняння фазових траєкторій Стан рівноваги визначається за умови у своїй x 0 = y 0 = 0. Особлива точка називається "центр" і відповідає стійкій рівновазі, так як фазові траєкторії від неї не видаляються. 2. Нехай коріння характеристичного рівняння (3) має вигляд При цьому перехідний процес описується рівняннями: З рівняння фазових траєкторій Це рівняння сімейства гіпербола при зміні A (рис 5). Усі інженерні методи дослідження нелінійних систем поділяються на дві основні групи: точні та наближені. До точних методів відноситься метод А. М. Ляпунова, метод фазової площини, метод точкових перетворень, частотний метод В. М. Попова. Наближені методи засновані на лінеаризації нелінійних рівнянь системи із застосуванням гармонійної чи статистичної лінеаризації. Насправді використовують комбінацію різних методів. Слід зазначити, що у найближчому майбутньому є необхідність подальшого розвитку теорії та практики нелінійних систем. Розглянемо такі методи аналізу нелінійних систем: 1) Метод фазової площини.Застосовується для дослідження нелінійних систем, що описуються диференціальними рівняннями першого та другого порядків. Складається у побудові та дослідженні фазового портрета системи в координатах досліджуваної величини та її похідної. Розглянемо випадок, коли зовнішній вплив дорівнює нулю (U = 0). Рух системи визначається зміною її координат - X iу функції часу. Значення X iу будь-який момент часу характеризує стан (фазу) системи та визначає координати системи, що має n – осей і можуть бути представлені як координати деякої (зображуючої) точки М (рис. 10). Малюнок 10 Фазовий простір називається простір координат системи. Зі зміною часу t точка М рухається по траєкторії, яка називається фазовою траєкторією. Якщо змінювати початкові умови отримаємо сімейство фазових траєкторій, які називаються фазовим портретом. Фазовий портрет визначає характер перехідного процесу у нелінійній системі. Фазовий портрет має особливі точки, яких прагнуть чи яких йдуть фазові траєкторії системи (їх може бути кілька). Фазовий портрет може містити замкнуті фазові траєкторії, які називаються граничними циклами. Граничні цикли характеризують автоколивання у системі. Фазові траєкторії ніде не перетинаються, крім спеціальних точок, що характеризують рівноважні стани системи. Граничні цикли та стану рівноваги можуть бути стійкими або нестійкими. Фазовий портрет повністю характеризує нелінійну систему. Характерною особливістю нелінійних систем є наявність різних типів рухів, кількох станів рівноваги, граничних циклів. приклад Зобразити фазові траєкторії для нелінійної системи з трьома різними нелінійностями - двопозиційне реле, трипозиційне реле із зоною нечутливості (±0,2) та двопозиційне реле з гістерезисом (±0,1), якщо лінійна частина має передатну функцію Рішення Відповідно до завдання модель нелінійної системи можна подати у вигляді рис.11. Приймемо всім нелінійностей величину сигналу на виході реле ±2. Малюнок 11 - Модель нелінійної САУ Тоді рівняння стану запишуться як Розділивши друге із рівнянь на перше, отримаємо рівняння фазової траєкторії Залежно від того, з якого боку від лінії перемикання реле знаходиться точка, що зображає, рішення диференціального рівняння будуть наступні: праворуч лінії перемикання при x1 > 0 x 1 = 4 ln |x 2 + 10| - 0,4 x 2 + c 1; зліва від лінії перемикання при x1< 0 x 1 = 4 ln |x 2 - 10| - 0,4x 2 + c 2 ; для трипозиційного реле рух зображувальної точки в межах зони нечутливості -0,2 де з 1, з 2 і з 3 - постійні інтегрування, що залежать від початкових умов. На рис. 9 зображено фазові траєкторії нелінійної САУ з різними нелінійними елементами. Припасовування або зшивання ділянок фазових траєкторій відбувається лініями перемикань. Малюнок 12 - Фазові траєкторії релейних систем Аналізуючи фазові траєкторії, можна зробити такі висновки: 1. за взятих початкових умов усі системи стійкі. Причому системи з двопозиційними реле стійкі у великому; 2. у систем із двопозиційними реле спостерігаються стійкі коливання. Абсциса граничного циклу визначає амплітуду коливань А, а частота може бути визначена з ординати граничного циклу А про о; 3. система з трипозиційним реле із зоною нечутливості має "особливий відрізок". Система може після перехідного процесу зайняти будь-яке значення всередині зони нечутливості, як показано на рис.9. p align="justify"> Таким чином, метод фазового простору є фундаментальним методом дослідження нелінійних систем. Дослідити нелінійних систем на фазовій площині набагато простіше та зручніше, ніж за допомогою побудови графіків перехідних процесів у часовій області. Геометричні побудови у просторі менш наочні, ніж побудови на площині, коли система має другий порядок, при цьому застосовується метод фазової площини. 2) Метод гармонійної лінеаризації. Ідея методу гармонійної лінеаризації належить Н.М. Крилову та Н.М. Боголюбову і базується на заміні нелінійного елемента системи лінійною ланкою, параметри якого визначаються при гармонійному вхідному впливі з умови рівності амплітуд перших гармонік на виході нелінійного елемента та еквівалентної лінійної ланки. p align="justify"> Метод є наближеним і може бути використаний тільки у випадку, коли лінійна частина системи є фільтром низьких частот, тобто. відфільтровує всі виникаючі на виході нелінійного елемента гармонійні складові, крім першої гармоніки. При цьому лінійна частина може бути описана диференціальним рівнянням будь-якого порядку, а нелінійний елемент може бути однозначним, так і багатозначним. Метод може бути ефективний для розрахунку параметрів власних коливань в системі, використовується також для аналізу точності при гармонійному впливі, що задає. У основі методу гармонійної лінеаризації лежить припущення, що у вхід нелінійного елемента подається гармонійний вплив із частотою і амплітудою А, тобто. x = А sin?t. У припущенні, що лінійна частина є фільтром низьких частот, спектр вихідного сигналу лінійної частини обмежується лише першою гармонікою, яка визначається поруч Фур'є (у цьому і полягає наближеність методу, тому що вищі гармоніки викидаються з розгляду). Тоді зв'язок між першою гармонікою вихідного сигналу та вхідним гармонійним впливом нелінійного елемента представляється у вигляді передавальної функції: Рівняння (1.6) називається рівнянням гармонійної лінеаризації, а коефіцієнти q і q" - коефіцієнтами гармонійної лінеаризації, що залежать від амплітуди А і частоти ω вхідного впливу. Слід зазначити. що для статичних однозначних коефіцієнт q"(А)=0. Піддавши рівняння (1.6) перетворення Лапласа при нульових початкових умовах з наступною заміною оператора p на jω (p = jω), отримаємо еквівалентний комплексний коефіцієнт передачі нелінійного елемента W не (jω,A) = q + jq" (1.7) Після того, як проведена гармонійна лінеаризація, для аналізу та синтезу нелінійних САУ можливе застосування всіх методів, що застосовуються для дослідження лінійних систем, у тому числі використання різних критеріїв стійкості. При дослідженні нелінійних систем на основі методу гармонійної лінеаризації насамперед вирішують питання про існування та стійкість періодичних (автоколивальних) режимів. Якщо періодичний режим стійкий, то в системі існують автоколивання з частотою 0 і амплітудою А 0 . Розглянемо нелінійну систему, що включає лінійну частину з передавальною функцією та нелінійний елемент з еквівалентним комплексним коефіцієнтом передачі (1.7). Розрахункова структурна схема нелінійної системи набуває вигляду рис.13. Малюнок 13 – Структурна схема нелінійної САУ Для оцінки можливості виникнення автоколивань у нелінійній системі методом гармонійної лінеаризації необхідно знайти умови межі стійкості, як це робилося під час аналізу стійкості лінійних систем. Якщо лінійна частина описується передатною функцією (1.8), а нелінійний елемент (1.7), то характеристичне рівняння замкнутої системи матиме вигляд: d(p) + k(p)(q(ω,A) + q"(ω,A)) = 0 (1.10) З критерію стійкості Михайлова кордоном стійкості буде проходження годографа Михайлова через початок координат. З виразів (1.10) можна знайти залежність амплітуди та частоти автоколивань від параметрів системи, наприклад, коефіцієнта передачі k лінійної частини системи. І тому необхідно рівняннях (1.10) коефіцієнт передачі k вважати змінної величиною, тобто. це рівняння записати у вигляді: d(jω) + K(jω)(q(ω,A) + q"(ω,A)) = Re(ω 0 ,A 0 ,K) +Jm(ω 0 ,A 0 ,k) = 0 ( 1.11) де ω o і A o - можливі частота та амплітуда автоколивань. Тоді, прирівнюючи до нуля дійсну та уявну частини рівняння (1.11) можна побудувати межу стійкості (D-розбиття) за цікавим для нас параметром k (рис.11). Рисунок 14 - D-розбиття площини параметра До нелінійної САУ Аналізуючи рис.14 можна зробити висновок, що в області 1 автоколивання неможливі і критичний коефіцієнт дорівнює до кр, а в області 2 коливання сходяться до величини амплітуди A o і частоти o (автоколивальний режим) в залежності від початкових умов. За графіком рис.11 можна вибрати коефіцієнт передачі k, у якому амплітуда і частота можливих автоколивань має допустимі значення чи взагалі відсутня. Найчастіше використовується графоаналітичний метод визначення можливих амплітуд і частот автоколивань у нелінійних системах. Відповідно до критерію стійкості Найквіста незагасаючі коливання в лінійній системі виникають у тому випадку, коли амплітудно-фазова характеристика розімкнутої системи проходить через точку з координатами . Ця умова є також умовою існування автоколивань гармонійно лінеаризованої нелінійної системі (рис.11), тобто. 1 + W лч (jω) * W не (jω, A) = 0 (1.13) або W лч (jω)=-1/W не (jω,A). (1.14) Рішення рівняння (1.14) щодо частоти та амплітуди автоколивань можна отримати графічно, як точку перетину годографа частотної характеристики лінійної частини системи Wлч(jω) та годографа зворотної характеристики нелінійної частини -1/Wне(jω,А) (рис. 15). Якщо ці годографи не перетинаються, режим автоколивань в досліджуваній системі немає. Рисунок 15- Годографи лінійної та нелінійної частин системи Для стійкості автоколивального режиму з частотою ω 0 і амплітудою А 0 потрібно, щоб точка на годографі нелінійної частини М, що відповідає збільшеній амплітуді А 0 +ΔА в порівнянні зі значенням в точці перетину годографів, не охоплювалася годографом частотної характеристики лінійної частини системи, в іншому автоколивання нестійкі. На рис. 15 наведено приклад розташування годографів для випадку, коли в нелінійній системі існують стійкі автоколивання. Параметри автоколивань на вході нелінійного елемента визначаються в точці перетину годографів: частота W лч (jω), а амплітуда з W не -1 (A). Дослідження нелінійних систем можливе за логарифмічними частотними характеристиками (метод шаблонів). Метод гармонійного балансу дозволяє вести синтез нелінійних САУ забезпечення необхідних показників якості змінюючи параметри або лінійної частини, або нелінійного елемента. приклад Визначити можливу частоту автоколивань при введенні в САУ, що має ЛЧХ виду (рисунок 16), однозначної нелінійності у вигляді двопозиційного реле. Малюнок 16 - ЛЧХ лінійної частини РішенняВідомо, що характеристика - 1/W не (jω,А) однозначного нелінійного елемента (двопозиційного реле) повністю розташовується на негативній дійсній півосі, тому а.ф.х. лінійної частини W лч (jω) може її перетнути тільки при вугіллі -180°. Частота можливих автоколивань визначається W лч (jω), а л.ф.х. (рис.7.8) показує, що фазовий кут зсуву -180 ° відбувається на частоті = 300 рад/с. Це і є можлива частота автоколивань під час введення в САУ однозначної нелінійності. p align="justify"> Метод гармонійної лінеаризації використовується для аналізу перехідних режимів роботи, оцінки стійкості системи, можливості виникнення періодичних коливань. 3) Метод статистичної лінеаризації. Метод заснований на заміні нелінійного перетворення процесів статистично еквівалентним їм лінійним перетворенням. Нелінійний елемент замінюється лінійним еквівалентом (рис. 17). Внаслідок заміни система лінеаризується, що дозволяє використовувати методи дослідження лінійних систем. Заміна нелінійного перетворення лінійним є наближеною та справедливою лише у деяких відносинах. Тому немає однозначної еквівалентності під час використання різних критеріїв. Зокрема, якщо нелінійність визначається безінерційною залежністю виду використовується два критерії еквівалентності. Малюнок 17 Перший критерій передбачає рівність на виході нелінійного елемента та його лінійного еквівалента математичних очікувань та дисперсій процесів. Другий критерій - мінімум середнього квадрата різниці процесів на виході нелінійного елемента та його лінійного еквівалента. Процес на вході та виході нелінійного елемента представимо у вигляді: де - математичне очікування процесу на виході НЕ; ─ центрована випадкова складова. Процес на виході лінійного еквівалента подається у такому вигляді: де - коефіцієнт передачі лінійного еквівалента з математичного очікування; ─ коефіцієнт передачі за центрованою випадковою складовою. Скористаємося першим критерієм еквівалентності: З цих рівнянь знаходимо де - щільність ймовірності процесу на вході нелінійного елемента. Коефіцієнт передачі лінійного еквівалента за центрованою випадковою складовою (за першим критерієм). За другим критерієм еквівалентності: Для визначення та , за яких виконується умова еквівалентності, знайдемо приватні похідні та прирівняємо їх нулю: При розрахунку цих коефіцієнтів вважають, що розподіл на вході нормальний: Визначивши величини для типових нелінійностей, замінюють останні коефіцієнтами передачі лінійного еквівалента та аналізують систему лінійними методами. Для основних типів нелінійностей та нормальному розподілі вхідного процесу коефіцієнти розраховані та представлені у вигляді табличних значень. Зокрема, характеристики релейного типу (рис.19) Рисунок 19 - Характеристика релейного типу: коефіцієнти рівні. "Теорія автоматичного керування" "Методи дослідження нелінійних систем" 1. Метод диференціальних рівнянь Диференціальне рівняння замкнутої нелінійної системи n-го порядку (рис. 1) можна перетворити на систему n-диференціальних рівнянь першого порядку як: де: - Змінні, що характеризують поведінку системи (одна з них може бути регульована величина); - Нелінійні функції; u - вплив, що задає. Зазвичай ці рівняння записуються в кінцевих різницях: де – Початкові умови. Якщо відхилення невеликі, то цю систему можна вирішувати як систему рівнянь алгебри. Рішення можна подати графічно. 2. Метод фазового простору Розглянемо випадок, коли зовнішній вплив дорівнює нулю (U = 0). Рух системи визначається зміною її координат – у функції часу. Значення у будь-який момент часу характеризує стан (фазу) системи та визначає координати системи, що має n – осей і можуть бути представлені як координати деякої (зображуючої) точки М (рис. 2). Фазовий простір називається простір координат системи. Зі зміною часу t точка М рухається по траєкторії, яка називається фазовою траєкторією. Якщо змінювати початкові умови отримаємо сімейство фазових траєкторій, які називаються фазовим портретом. Фазовий портрет визначає характер перехідного процесу у нелінійній системі. Фазовий портрет має особливі точки, яких прагнуть чи яких йдуть фазові траєкторії системи (їх може бути кілька). Фазовий портрет може містити замкнуті фазові траєкторії, які називаються граничними циклами. Граничні цикли характеризують автоколивання у системі. Фазові траєкторії ніде не перетинаються, крім спеціальних точок, що характеризують рівноважні стани системи. Граничні цикли та стану рівноваги можуть бути стійкими або нестійкими. Фазовий портрет повністю характеризує нелінійну систему. Характерною особливістю нелінійних систем є наявність різних типів рухів, кількох станів рівноваги, граничних циклів. p align="justify"> Метод фазового простору є фундаментальним методом дослідження нелінійних систем. Дослідити нелінійних систем на фазовій площині набагато простіше та зручніше, ніж за допомогою побудови графіків перехідних процесів у часовій області. Геометричні побудови у просторі менш наочні, ніж побудови на площині, коли система має другий порядок, при цьому застосовується метод фазової площини. Застосування методу фазової площини для лінійних систем Проаналізуємо зв'язок між характером перехідного процесу та кривими фазових траєкторій. Фазові траєкторії можуть бути отримані шляхом інтегрування рівняння фазової траєкторії, або шляхом вирішення вихідного диференціального рівняння 2-го порядку. Нехай задано систему (рис. 3). Розглянемо вільний рух системи. У цьому: U(t)=0, e(t)=– x(t) У загальному вигляді диференціальне рівняння має вигляд Це однорідне диференціальне рівняння 2-го порядку його характеристичне рівняння одно Коріння характеристичного рівняння визначається із співвідношень Представимо диференціальне рівняння 2-го порядку як системи рівнянь 1-го порядку: де швидкість зміни регульованої величини. У лінійній системі, що розглядається, змінні x і y являють собою фазові координати. Фазовий портрет будуємо у просторі координат x і y, тобто. на фазовій площині. Якщо виключимо час із рівняння (1), то отримаємо рівняння інтегральних кривих чи фазових траєкторій. Це рівняння з змінними, що розділяються Розглянемо кілька випадків Файлів GB_prog.m та GB_mod.mdl, а аналіз спектрального складу періодичного режиму на виході лінійної частини – за допомогою файлів GB_prog.m та R_Fourie.mdl. Зміст файлу GB_prog.m: %Дослідження нелінійних систем методом гармонійного балансу %Використані файли: GB_prog.m, GB_mod.mdl та R_Fourie.mdl. %Позначення, що використовуються: НЕ - нелінійний елемент, ЛЧ - лінійна частина. %Очищення всіх... Безінерційний у допустимому (обмеженому зверху) діапазоні частот, при виході за межі якого він переходить у розряд інерційних. Залежно від виду характеристик розрізняють нелінійні елементи із симетричними та несиметричними характеристиками. Симетричною називається характеристика, яка залежить від напряму визначальних її величин, тобто. має симетрію щодо початку системи...
 і кут перетину фазової траєкторією ізокліни за формулою a = arctg c, результати наведені в таблицях 1 і 2.
і кут перетину фазової траєкторією ізокліни за формулою a = arctg c, результати наведені в таблицях 1 і 2.Таблиця 1
Таблиця 2

Приклад 4. Для заданої системи (рис. 26) побудувати зразковий фазовий портрет.







 і кут перетину фазової траєкторією ізокліни за формулою a = arctg c.
і кут перетину фазової траєкторією ізокліни за формулою a = arctg c.



 де
де  (1)
(1)
![]() . (2)
. (2)
 (3)
(3)
 (4) швидкість зміни регульованої величини.
(4) швидкість зміни регульованої величини.  . (5)
. (5)
Розглянемо кілька випадків
![]() ). (7)
). (7)
 (9)
(9)
 ,
,
![]() отримаємо рівняння
отримаємо рівняння 






 де
де  (1)
(1)![]() . (2)
. (2) (3)
(3) (4)
(4) . (5)
. (5)









 Історія пілотів, які бомбили Хіросіму і Нагасакі
Історія пілотів, які бомбили Хіросіму і Нагасакі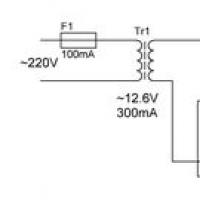 Плавний заряд ємності: що вибрати?
Плавний заряд ємності: що вибрати?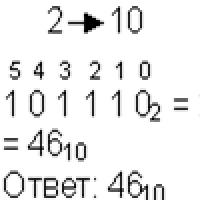 Малий математичний факультет
Малий математичний факультет «Хоровод до чого сниться уві сні?
«Хоровод до чого сниться уві сні? До чого сниться церква всередині: тлумачення значення сну з різних сонників для чоловіків і жінок
До чого сниться церква всередині: тлумачення значення сну з різних сонників для чоловіків і жінок Сонник хурма, до чого сниться хурма уві сні бачити Хурма уві сні до чого
Сонник хурма, до чого сниться хурма уві сні бачити Хурма уві сні до чого Зачарована душа Значення кармічних цифр
Зачарована душа Значення кармічних цифр