Gleichung der Näherungsgeraden. Methoden zur Approximation der Eigenschaften nichtlinearer Elemente. Hochpräzise und schöne Ersetzung von Tabellendaten durch eine einfache Gleichung
Lineare, insbesondere lineare Polynomnäherungen entsprechen oft nicht der Natur der Funktion. Beispielsweise wächst ein Polynom hohen Grades schnell und daher wird selbst eine einfache Funktion auf einem großen Segment schlecht durch das Polynom angenähert. Da die Approximation über einen weiten Bereich von Argumentänderungen erfolgt, ist die Verwendung einer nichtlinearen Abhängigkeit von den Koeffizienten hier noch vorteilhafter als bei der Interpolation.
In der Praxis werden zwei Arten von Abhängigkeiten verwendet. Eine davon ist eine quasilineare Abhängigkeit, die durch eine nivellierende Änderung der Variablen auf eine lineare Abhängigkeit reduziert wird, die in den vorherigen Absätzen ausführlich untersucht wurde. Diese Methode ist sehr effektiv und wird häufig bei der Verarbeitung von Experimenten verwendet, da a priori Informationen über die Physik des Prozesses dabei helfen, einen guten Ersatz für Variablen zu finden. Wir müssen nur bedenken, dass die Näherung, die in den neuen Variablen am besten ist, nicht die beste im Sinne des Skalarprodukts in den alten Variablen sein wird. Daher muss der Wahl der Gewichte in neuen Variablen besondere Aufmerksamkeit gewidmet werden.
Ein klassisches Beispiel ist das Problem des radioaktiven Zerfalls einer bestrahlten Probe, bei dem die geeigneten Variablen und t die Zerfallsrate sind. Bei diesen Variablen wird die Kurve üblicherweise durch eine gestrichelte Linie angenähert, deren Verknüpfungen dem Zerfall zunehmend langlebigerer Mitglieder der radioaktiven Reihe entsprechen.
Eine weitere häufig verwendete Art der Abhängigkeit von Koeffizienten ist die fraktional-lineare Abhängigkeit, wenn die Näherungsfunktion rational ist:
Häufig wird auch das Verhältnis verallgemeinerter Polynome verwendet. Diese Näherung ermöglicht es uns, die Pole der Funktion zu vermitteln – sie entsprechen den Nullstellen des Nenners der erforderlichen Multiplizität. Aufgrund der geeigneten Wahl der Größe ist es oft möglich, das asymptotische Verhalten bei zu reproduzieren, zum Beispiel wenn, dann müssen wir setzen. In diesem Fall können Sie sie groß genug annehmen, um viele Näherungskoeffizienten zu haben.
Der quadratische Fehler ist jedoch keine quadratische Funktion der Koeffizienten mehr, sodass es nicht einfach ist, die Koeffizienten einer rationalen Funktion zu finden. In Analogie zur quadratischen Mittelwertnäherung durch Polynome können wir annehmen, dass der Fehler eine Anzahl von Nullstellen hat, die nicht geringer ist als die Anzahl der freien Koeffizienten (vergleiche mit Bemerkung 3 in Absatz 2). Dann wird das Problem auf die Lagrange-Interpolation über diese Nullstellen reduziert und die Koeffizienten werden aus einem System linearer Gleichungen ermittelt:
Natürlich ist die genaue Position der Nullen unbekannt; Sie werden zufällig ausgewählt und normalerweise gleichmäßig über das Segment verteilt. Diese Methode wird als Methode der ausgewählten Punkte bezeichnet. Die mit dieser Methode erhaltene Näherung wird überhaupt nicht die beste sein.
Darüber hinaus ist die Methode der ausgewählten Punkte unzumutbar, ebenso wie jede Interpolation, wenn sie einen erkennbaren Fehler aufweist.
Die beste Näherung kann mit der iterierten Gewichtsmethode gefunden werden. Beachten Sie, dass die Aufgabe
lässt sich leicht lösen: Der Ausdruck links ist eine quadratische Funktion der Koeffizienten und die Differenzierung nach ihnen führt zu einem linearen System zur Bestimmung der Koeffizienten, ähnlich wie (38). Das neue Problem unterscheidet sich vom ursprünglichen Problem im Wesentlichen dadurch, dass anstelle eines Gewichts ein anderes Gewicht verwendet wird, sodass seine Lösung nicht die beste Näherung darstellt. Schreiben wir das ursprüngliche Problem in einer neuen Form:

und wir werden es durch einen einfachen iterativen Prozess lösen

kann als Nullnäherung angenommen werden. Bei jeder Iteration ist die Gewichtung aus der vorherigen Iteration bekannt, sodass die Koeffizienten leicht aus der Minimalbedingung der quadratischen Form ermittelt werden können. Die Praxis zeigt, dass die Koeffizienten der besten Näherung nur schwach von der Wahl des Gewichts abhängen, sodass die Iterationen normalerweise schnell konvergieren.
a) Betrachten Sie einige Beispiele für die Approximation durch eine rationale Funktion. Lasst uns
Wenn wir die ersten beiden Terme der Reihe durch einen Bruch ersetzen, erhalten wir . Diese einfache Formel gewährleistet Genauigkeit und ist für Schätzungen sehr praktisch.
b) In der Wahrscheinlichkeitstheorie spielt das Fehlerintegral, für das Reihenentwicklungen bekannt sind, eine wichtige Rolle:

Die erste Reihe konvergiert absolut, aber die Konvergenz ist sehr langsam; die zweite Reihe konvergiert asymptotisch für große Werte von . Ersetzen wir die ersten Terme jeder Reihe durch Brüche, erhalten wir

In den angegebenen Bereichen der Argumentänderung überschreitet der Fehler der ersten Formel nicht 0,4 % und der Fehler der zweiten Formel nicht mehr als 2,4 %. Somit ist die Genauigkeit dieser Näherungen für viele praktische Anwendungen völlig ausreichend.
c) Setzen wir auf . Diese Funktion ist monoton und es ist einfach, einen Bruch zu konstruieren
![]()
Approximation einer nichtlinearen Funktion
x 0 /12 /6 /4 /3 5/12 /2
J 0,5 0,483 0,433 0,354 0,25 0,129 0
Da das Partitionierungsintervall der Funktion gleich ist, berechnen wir die folgenden Steigungskoeffizienten der entsprechenden Abschnitte der angenäherten Funktion:

1. Konstruktion von Blöcken zur Bildung von Segmenten der Näherungsfunktion
Bildung der Zeitfunktion
Wechselintervall:
Zyklische Neustartzeit: T = 1s
Jetzt modellieren wir die Funktion:

Annäherung


Abbildung 3.1 – Schema zur Lösung der Gleichung
Abbildung 3.2 – Blockdiagramm der Bildung einer nichtlinearen Funktion
Somit wird automatisch die linke Seite der Gleichung gebildet. In diesem Fall geht man üblicherweise davon aus, dass die höchste Ableitung x// bekannt ist, da die Terme auf der rechten Seite der Gleichung bekannt sind und mit den Eingängen von U1 verbunden werden können (Abbildung 3.1). Der Operationsverstärker U3 fungiert als +x-Signalinverter. Um x// zu simulieren, ist es notwendig, einen weiteren Unterverstärker in die Schaltung einzuführen, an dessen Eingänge Signale angelegt werden müssen, die die rechte Seite der Gleichung (3.2) simulieren.
Die Skalen aller Variablen werden unter Berücksichtigung der Tatsache berechnet, dass der Maximalwert der Maschinenvariablen über dem Absolutwert hinaus 10 V beträgt:
Mx = 10 / xmax; Mx/ = 10 / x/ max; Mx // = 10 / x //max;
My = 10 / ymax. (3.3)
Zeitskala Mt = T / tmax = 1, da das Problem in Echtzeit simuliert wird.
Die Übertragungskoeffizienten für jeden Eingang der integrierenden Verstärker werden berechnet.
Für den Verstärker U1 werden die Übertragungskoeffizienten anhand der Formeln ermittelt:
K11 = Mx/ b / (MyMt); K12 = Mx/ a2 / (MxMt);
K13 = Mx/ a1 / (MxMt). (3.4)
Für Verstärker U2:
K21 = Mx/ / (Mx/ Mt), (3.5)
und für Verstärker U3:
K31 = 1. (3.6)
Die Spannungen der Anfangsbedingungen werden nach den Formeln berechnet:
ux/ (0) = Mx/ x/ (0) (-1); ux(0)= Mxx(0) (+1). (3.7)
Die rechte Seite der Gleichung (3.2) wird durch eine nichtlineare Funktion dargestellt, die durch lineare Näherung spezifiziert wird. In diesem Fall muss überprüft werden, dass der Näherungsfehler einen vorgegebenen Wert nicht überschreitet. Das Blockdiagramm der Bildung einer nichtlinearen Funktion ist in Abbildung 3.2 dargestellt.
Beschreibung des Schaltplans
Der Block zur Erzeugung der Zeitfunktion (Ф) besteht aus einem (zur Bildung von t) oder zwei in Reihe geschalteten (zur Bildung von t2) integrierenden Verstärkern mit Null-Anfangsbedingungen.
Wenn in diesem Fall ein Signal U an den Eingang des ersten Integrators angelegt wird, erhalten wir an seinem Ausgang:
u1(t)= - K11 = - K11Et. (3.8)
Wenn wir K11E=1 setzen, gilt u1(t)= t.
Am Ausgang des zweiten Integrators erhalten wir:
u2(t)= K21 = K11K21Et2 / 2 (3.9)
Wenn wir K11K21E/2 = 1 setzen, gilt u2(t)= t2.
Blöcke zur Bildung von Segmenten der Näherungsfunktion werden in Form von Diodenblöcken nichtlinearer Funktionen (DBNF) implementiert, deren Eingangswert eine Funktion der Zeit t oder t2 ist. Das Verfahren zur Berechnung und Konstruktion von DBNF ist in angegeben.
Der Addierer (SAD) der Segmente der Näherungsfunktion ist in Form eines Differenzendverstärkers ausgeführt.
Die Anfangsbedingungen für die Integratoren der Modellierungsschaltung werden anhand eines Knotens mit variabler Struktur eingeführt (Abbildung 3.3). Dieses Schema kann in zwei Modi funktionieren:
a) Integration – mit Taste K in Position 1. In diesem Fall wird das ursprüngliche Signal der Schaltung mit ausreichender Genauigkeit durch die Gleichung eines idealen Integrators beschrieben:
u1(t)= - (1 / RC) . (3.10)
Dieser Modus wird beim Modellieren einer Aufgabe verwendet. Um die Richtigkeit der Wahl der Parameter R und C des Integrators zu überprüfen, überprüfen Sie den Wert der Anfangsspannung des Integrators als Funktion der Zeit und der nützlichen Integrationszeit innerhalb des zulässigen Fehlers? Uperm.
Die Größe der anfänglichen Integratorspannung
U(t)= - KYE (1 - e - T / [(Ky+1)RC) (3.11)
Während der Simulation sollte T bei der Integration des Eingangssignals E mit einem Operationsverstärker mit einer Verstärkung Ky ohne Rückkopplungsschaltung den Wert der Maschinenvariablen (10 V) nicht überschreiten.
Integrationszeit
Ti = 2RC(Kу + 1)?Uadd (3.12)
mit den gewählten Schaltungsparametern sollte nicht kleiner als die Simulationszeit T sein.
b) Die Einstellung der Anfangsbedingungen erfolgt durch Umschalten des Schlüssels K auf Position 2. Dieser Modus wird bei der Vorbereitung der Modellierungsschaltung für den Lösungsprozess verwendet. In diesem Fall wird das ursprüngliche Signal der Schaltung durch die Gleichung beschrieben:
u0(t)= - (R2 /R1) E (3.13)
wobei u0(t) der Wert der Anfangsbedingungen ist.
Um die Zeit zur Bildung der Anfangsbedingungen zu verkürzen und einen zuverlässigen Betrieb zu gewährleisten, müssen die Schaltungsparameter die Bedingung erfüllen: R1C1 = R2C.
Erstellen Sie ein vollständiges Berechnungsschema. In diesem Fall sollten Sie die in Abschnitt 3.1 angegebenen Symbole verwenden.
Erstellen Sie unter Verwendung der Bittiefe der Eingangs- und Quelldaten Schaltpläne der Blöcke B1 und B2 und verbinden Sie diese mit dem RS-Block.
(Bitte beachten Sie den zusätzlichen Abschnitt vom 04.06.2017 am Ende des Artikels.)
Buchhaltung und Kontrolle! Die über 40-Jährigen sollten sich diesen Slogan aus der Zeit des Aufbaus des Sozialismus und Kommunismus in unserem Land gut merken.
Aber ohne eine fundierte Buchführung ist das effektive Funktionieren eines Landes, einer Region, eines Unternehmens oder eines Haushalts in keiner sozioökonomischen Form der Gesellschaft möglich! Um Prognosen und Pläne für Aktivität und Entwicklung zu erstellen, sind Ausgangsdaten erforderlich. Wo kann ich sie bekommen? Nur einer zuverlässig Quelle ist dein statistische Aufzeichnungen früherer Zeiträume.
Nach meinem Verständnis sollte jeder vernünftige Mensch die Ergebnisse seiner Aktivitäten berücksichtigen, Informationen sammeln und aufzeichnen, Daten verarbeiten und analysieren und die Analyseergebnisse anwenden, um in Zukunft die richtigen Entscheidungen zu treffen. Dies ist nichts anderes als die Anhäufung und rationale Nutzung der eigenen Lebenserfahrung. Wenn Sie keine Aufzeichnungen über wichtige Daten führen, werden Sie diese nach einer gewissen Zeit vergessen und wenn Sie sich erneut mit diesen Problemen befassen, werden Sie wieder dieselben Fehler machen, die Sie beim ersten Mal gemacht haben.
„Ich erinnere mich, dass wir vor fünf Jahren bis zu 1000 Stück solcher Produkte pro Monat hergestellt haben und jetzt kaum noch 700 zusammenbauen können!“ Wir öffnen die Statistik und sehen, dass vor 5 Jahren noch nicht einmal 500 Stück produziert wurden...
„Wie viel kostet ein Kilometer Ihres Autos unter Berücksichtigung? alle Kosten? Öffnen wir die Statistik – 6 Rubel/km. Fahrt zur Arbeit – 107 Rubel. Mehr als das Eineinhalbfache billiger als ein Taxi (180 Rubel). Und es gab Zeiten, da war es günstiger, ein Taxi zu nehmen ...
„Wie lange dauert die Herstellung der Stahlkonstruktionen eines 50 m hohen Eckfernmeldeturms?“ Wir öffnen die Statistik – und in 5 Minuten ist die Antwort fertig...
„Wie viel kostet die Renovierung eines Zimmers in einer Wohnung?“ Wir rufen alte Aufzeichnungen ab, nehmen eine Anpassung an die Inflation der letzten Jahre vor, berücksichtigen, dass wir das letzte Mal Materialien gekauft haben, die 10 % günstiger als der Marktpreis waren, und wir kennen bereits die geschätzten Kosten ...
Indem Sie Aufzeichnungen über Ihre beruflichen Aktivitäten führen, sind Sie immer bereit, die Frage Ihres Chefs zu beantworten: „Wann!!!???“ Durch die Führung von Haushaltsunterlagen ist es einfacher, künftige Ausgaben für große Anschaffungen, Urlaube und andere Ausgaben zu planen und bereits heute geeignete Maßnahmen zu ergreifen, um ein zusätzliches Einkommen zu erzielen oder unnötige Ausgaben zu reduzieren.
In diesem Artikel werde ich anhand eines einfachen Beispiels zeigen, wie gesammelte statistische Daten in Excel verarbeitet werden können, um sie für die Prognose zukünftiger Zeiträume weiterzuverwenden.
Approximation statistischer Daten in Excel mit einer Analysefunktion.
Der Produktionsstandort produziert Baumetallkonstruktionen aus Blech- und Profilprodukten. Der Standort läuft stabil, die Aufträge sind gleichartig, die Zahl der Mitarbeiter schwankt leicht. Es liegen Daten zur Produktproduktion der letzten 12 Monate und zur Menge des in diesen Zeiträumen verarbeiteten Walzmetalls nach Gruppen vor: Bleche, I-Träger, Kanäle, Winkel, Rundrohre, Rechteckprofile, Rundprodukte. Nach einer vorläufigen Analyse der Ausgangsdaten kam man zu der Annahme, dass die monatliche Gesamtproduktion von Metallkonstruktionen maßgeblich von der Anzahl der Winkel in den Bestellungen abhängt. Überprüfen wir diese Annahme.
Zunächst ein paar Worte zur Annäherung. Wir werden nach einem Gesetz suchen – einer analytischen Funktion, also einer durch eine Gleichung spezifizierten Funktion, die besser als andere die Abhängigkeit der Gesamtproduktion von Metallkonstruktionen von der Menge an Winkelstahl in abgeschlossenen Aufträgen beschreibt. Dies ist eine Näherung, und die gefundene Gleichung wird als Näherungsfunktion für die ursprüngliche Funktion bezeichnet, die in Form einer Tabelle angegeben ist.
1. Schalten Sie Excel ein und platzieren Sie eine Tabelle mit Statistikdaten auf einem Blatt.

2. Als nächstes erstellen und formatieren wir ein Streudiagramm, in dem wir entlang der X-Achse die Werte des Arguments festlegen – die Anzahl der verarbeiteten Ecken in Tonnen. Entlang der Y-Achse tragen wir die Werte der ursprünglichen Funktion ein – die in der Tabelle angegebene Gesamtproduktion von Metallkonstruktionen pro Monat.

3. Wir „zeigen“ mit der Maus auf einen beliebigen Punkt im Diagramm und klicken mit der rechten Maustaste, um das Kontextmenü aufzurufen (wie einer meiner guten Freunde sagt – wenn Sie in einem unbekannten Programm arbeiten, wenn Sie nicht wissen, was Sie tun sollen, öfter mit der rechten Maustaste klicken...). Wählen Sie im Dropdown-Menü „Trendlinie hinzufügen...“.
4. Wählen Sie im angezeigten Fenster „Trendlinie“ auf der Registerkarte „Typ“ die Option „Linear“.


6. Im Diagramm erschien eine gerade Linie, die unserer Tabellenabhängigkeit nahe kam.

Zusätzlich zur Geraden selbst sehen wir die Gleichung dieser Geraden und vor allem den Wert des Parameters R 2 – den Wert der Zuverlässigkeit der Näherung! Je näher ihr Wert bei 1 liegt, desto genauer nähert sich die ausgewählte Funktion den Tabellendaten an!
7. Wir erstellen Trendlinien mithilfe von Potenz-, logarithmischen, exponentiellen und polynomialen Näherungen auf die gleiche Weise, wie wir eine lineare Trendlinie erstellt haben.

Von allen ausgewählten Funktionen nähert sich ein Polynom zweiten Grades unseren Daten am besten an; es hat den maximalen Zuverlässigkeitskoeffizienten R 2 .
Ich möchte Sie jedoch warnen! Wenn Sie Polynome höheren Grades verwenden, erhalten Sie wahrscheinlich noch bessere Ergebnisse, aber die Kurven sehen verschachtelt aus ... Hier ist es wichtig zu verstehen, dass wir nach einer Funktion suchen, die eine physikalische Bedeutung hat. Was bedeutet das? Dies bedeutet, dass wir eine Näherungsfunktion benötigen, die nicht nur innerhalb des betrachteten Bereichs von X-Werten, sondern auch darüber hinaus angemessene Ergebnisse liefert, d Die verarbeiteten Winkel pro Monat betragen weniger als 45 und mehr als 168 Tonnen! Daher empfehle ich nicht, sich von Polynomen hohen Grades mitreißen zu lassen und eine Parabel (Polynom zweiten Grades) sorgfältig auszuwählen!
Wir müssen also eine Funktion wählen, die nicht nur die Tabellendaten innerhalb des Wertebereichs X = 45...168 gut interpoliert, sondern auch eine angemessene Extrapolation außerhalb dieses Bereichs ermöglicht. In diesem Fall wähle ich eine logarithmische Funktion, Sie können aber auch eine lineare Funktion wählen, da diese die einfachste ist. Im betrachteten Beispiel sind die Fehler bei der Wahl einer linearen Näherung in Excel größer als bei der Wahl einer logarithmischen Näherung, jedoch nicht viel.
8. Wir entfernen alle Trendlinien aus dem Diagrammfeld, mit Ausnahme der logarithmischen Funktion. Klicken Sie dazu mit der rechten Maustaste auf unnötige Zeilen und wählen Sie im erscheinenden Kontextmenü „Löschen“.
9. Abschließend fügen wir den tabellarischen Datenpunkten Fehlerbalken hinzu. Klicken Sie dazu mit der rechten Maustaste auf einen der Punkte im Diagramm, wählen Sie im Kontextmenü „Datenreihen formatieren…“ und konfigurieren Sie die Daten auf der Registerkarte „Y-Fehler“ wie in der Abbildung unten.

10. Klicken Sie dann mit der rechten Maustaste auf eine der Fehlerbereichslinien, wählen Sie im Kontextmenü „Fehlerbalken formatieren…“ und passen Sie im Fenster „Fehlerbalken formatieren“ auf der Registerkarte „Ansicht“ die Farbe und Dicke der Linien an.

Alle anderen Diagrammobjekte werden auf die gleiche Weise formatiert.Excel!
Das Endergebnis des Diagramms ist im folgenden Screenshot dargestellt.

Ergebnisse.
Das Ergebnis aller vorherigen Aktionen war die resultierende Formel für die Näherungsfunktion y=-172,01*ln (x)+1188,2. Wenn man es und die Anzahl der Ecken im monatlichen Arbeitspaket kennt, ist es mit hoher Wahrscheinlichkeit (±4 % - siehe Fehlerbalken) möglich, die Gesamtproduktion von Metallkonstruktionen für den Monat vorherzusagen! Wenn der Plan für den Monat beispielsweise 140 Tonnen Winkel vorsieht, wird die Gesamtproduktion unter sonst gleichen Bedingungen höchstwahrscheinlich 338 ± 14 Tonnen betragen.
Um die Zuverlässigkeit der Näherung zu erhöhen, sollten viele statistische Daten vorliegen. Zwölf Wertepaare reichen nicht aus.
Aus der Praxis werde ich sagen, dass das Finden einer Näherungsfunktion mit einem Zuverlässigkeitskoeffizienten R 2 >0,87 als gutes Ergebnis angesehen werden sollte. Ein hervorragendes Ergebnis liegt bei R 2 >0,94.
In der Praxis kann es schwierig sein, einen der wichtigsten bestimmenden Faktoren zu identifizieren (in unserem Beispiel die Masse der in einem Monat bearbeiteten Ecken), aber wenn Sie es versuchen, können Sie ihn immer in jeder spezifischen Aufgabe finden! Natürlich hängt die Gesamtleistung für einen Monat wirklich von Hunderten von Faktoren ab, deren Berücksichtigung erhebliche Arbeitskosten von Standardsetzern und anderen Spezialisten erfordert. Aber das Ergebnis wird immer noch ungefähr sein! Lohnt es sich also, die Kosten zu tragen, wenn es weitaus günstigere mathematische Modelle gibt?
In diesem Artikel habe ich nur die Spitze des Eisbergs gestreift, nämlich die Erhebung, Verarbeitung und praktische Nutzung statistischer Daten. Ob es mir gelungen ist, Ihr Interesse für dieses Thema zu wecken, hoffe ich anhand der Kommentare und Bewertungen des Artikels in Suchmaschinen herauszufinden.
Das aufgeworfene Problem der Approximation einer Funktion einer Variablen hat in verschiedenen Lebensbereichen breite praktische Anwendung. Aber die Lösung des Funktionsnäherungsproblems hat eine viel größere Anwendung mehrere unabhängige Variablen... Lesen Sie darüber und mehr in den folgenden Blogartikeln.
Abonnieren zu Ankündigungen von Artikeln im Fenster am Ende jedes Artikels oder im Fenster oben auf der Seite.
Nicht vergessen bestätigen Abonnieren Sie, indem Sie auf den Link klicken in einem Brief, der Ihnen an der angegebenen Poststelle zugeht (kann im Ordner ankommen). « Spam » )!!!
Ich werde Ihre Kommentare mit Interesse lesen, liebe Leser! Schreiben!
P.S. (06.04.2017)
Hochpräzise und schöne Ersetzung von Tabellendaten durch eine einfache Gleichung.
Sie sind mit der erhaltenen Näherungsgenauigkeit nicht zufrieden (R 2<0,95) или вид и набор функций, предлагаемые MS Excel?
Sind die Dimensionen des Ausdrucks und die Linienform des hochgradig approximierenden Polynoms für das Auge nicht angenehm?
Bitte besuchen Sie die Seite „“, um ein genaueres und kompakteres Ergebnis der Approximation Ihrer Tabellendaten zu erhalten und eine einfache Technik zum Lösen von Problemen der hochpräzisen Approximation durch eine Funktion einer Variablen zu erlernen.

Bei Verwendung des vorgeschlagenen Aktionsalgorithmus wurde eine sehr kompakte Funktion gefunden, die die höchste Näherungsgenauigkeit bietet: R 2 =0,9963!!!
Numerische Methoden zur Lösung von Problemen
Radiophysik und Elektronik
(Lernprogramm)
Woronesch 2009
Das Lehrbuch wurde am Lehrstuhl für Physikalische Elektronik erstellt
Fakultät der Staatlichen Universität Woronesch.
Berücksichtigt werden Methoden zur Lösung von Problemen im Zusammenhang mit der automatisierten Analyse elektronischer Schaltkreise. Die Grundkonzepte der Graphentheorie werden vorgestellt. Es wird eine matrixtopologische Formulierung der Kirchhoffschen Gesetze gegeben. Die bekanntesten Methoden der Matrixtopologie werden beschrieben: die Methode der Knotenpotentiale, die Methode der Schleifenströme, die Methode der diskreten Modelle, die Hybridmethode, die Methode der variablen Zustände.
1. Approximation nichtlinearer Eigenschaften. Interpolation. 6
1.1. Newton- und Lagrange-Polynome 6
1.2. Spline-Interpolation 8
1.3. Methode der kleinsten Quadrate 9
2. Systeme algebraischer Gleichungen 28
2.1. Systeme linearer Gleichungen. Gauß-Methode. 28
2.2. Spärliche Gleichungssysteme. LU-Faktorisierung. 36
2.3. Nichtlineare Gleichungen lösen 37
2.4. Lösen von Systemen nichtlinearer Gleichungen 40
2.5. Differentialgleichung. 44
2. Methoden zur Suche nach Extremwerten. Optimierung. 28
2.1. Extremum-Suchmethoden. 36
2.2. Passive Suche 28
2.3. Sequentielle Suche 36
2.4. Mehrdimensionale Optimierung 37
Referenzen 47
Approximation nichtlinearer Eigenschaften. Interpolation.
1.1. Newton- und Lagrange-Polynome.
Bei der Lösung vieler Probleme wird es notwendig, eine Funktion f, über die unvollständige Informationen vorliegen oder deren Form zu komplex ist, durch eine einfachere und praktischere Funktion F zu ersetzen, die in der einen oder anderen Hinsicht f nahe kommt und ihren Näherungswert angibt Darstellung. Zur Näherung (Näherung) werden Funktionen F einer bestimmten Klasse verwendet, beispielsweise algebraische Polynome eines bestimmten Grades. Es gibt viele verschiedene Versionen des Funktionsnäherungsproblems, abhängig davon, welche Funktionen f approximiert werden, welche Funktionen F zur Approximation verwendet werden, wie die Nähe der Funktionen f und F verstanden wird usw.
Eine der Methoden zur Konstruktion von Näherungsfunktionen ist die Interpolation, wenn es erforderlich ist, dass an bestimmten Punkten (Interpolationsknoten) die Werte der ursprünglichen Funktion f und der Näherungsfunktion F übereinstimmen. Im allgemeineren Fall sind die Werte von Die Ableitungen an bestimmten Punkten müssen übereinstimmen.
Funktionsinterpolation wird verwendet, um eine schwer zu berechnende Funktion durch eine andere zu ersetzen, die einfacher zu berechnen ist; zur ungefähren Wiederherstellung einer Funktion aus ihren Werten an einzelnen Punkten; zur numerischen Differentiation und Integration von Funktionen; zur numerischen Lösung nichtlinearer und Differentialgleichungen etc.
Das einfachste Interpolationsproblem ist wie folgt. Für eine bestimmte Funktion auf einem Segment werden n+1 Werte an Punkten angegeben, die als Interpolationsknoten bezeichnet werden. Dabei . Es ist erforderlich, eine Interpolationsfunktion F(x) zu konstruieren, die an den Interpolationsknoten dieselben Werte wie f(x) annimmt:
F(x 0) = f(x 0), F(x 1) = f(x 1), ... , F(x n) = f(x n)
Geometrisch bedeutet dies, eine Kurve eines bestimmten Typs zu finden, die durch ein gegebenes Punktsystem (x i, y i) verläuft, i = 0,1,…,n.
Wenn die Werte des Arguments über den Bereich hinausgehen, dann sprechen wir von Extrapolation – der Fortsetzung der Funktion über den Bereich ihrer Definition hinaus.
Am häufigsten wird die Funktion F(x) in Form eines algebraischen Polynoms konstruiert. Es gibt verschiedene Darstellungen algebraischer Interpolationspolynome.
Eine der Methoden zum Interpolieren von Funktionen, die Werte an Punkten annehmen, besteht darin, ein Lagrange-Polynom zu konstruieren, das die folgende Form hat:
Der Grad des Interpolationspolynoms, das n+1 Interpolationsknoten durchläuft, ist gleich n.
Aus der Form des Lagrange-Polynoms folgt, dass das Hinzufügen eines neuen Knotenpunkts zu einer Änderung aller Terme des Polynoms führt. Dies ist die Unannehmlichkeit von Lagranges Formel. Die Lagrange-Methode enthält jedoch eine Mindestanzahl arithmetischer Operationen.
Um Lagrange-Polynome steigenden Grades zu konstruieren, kann das folgende Iterationsschema (Aitken-Schema) verwendet werden.
Polynome, die durch zwei Punkte (x i , y i), (x j , y j) (i=0,1,…,n-1 ; j=i+1,…,n) verlaufen, können wie folgt dargestellt werden:
Polynome, die durch drei Punkte verlaufen (x i , y i) , (x j , y j) , (x k , y k)
(i=0,…,n-2 ; j=i+1,…,n-1 ; k=j+1,…,n), kann durch die Polynome L ij und L jk ausgedrückt werden:
Polynome für vier Punkte (x i, y i), (x j, y j), (x k, y k), (x l, y l) werden aus den Polynomen L ijk und L jkl konstruiert:
Der Prozess wird fortgesetzt, bis ein Polynom erhalten wird, das durch n gegebene Punkte verläuft.
Der Algorithmus zur Berechnung des Wertes des Lagrange-Polynoms am Punkt XX, der das Aitken-Schema implementiert, kann mit dem Operator geschrieben werden:
für (int i=0;i für (int i=0;i<=N-2;i++)Здесь не нужно слово int, программа es wird als Fehler wahrgenommen – wiederholte Deklaration der Variablen, Variable i wurde bereits deklariert für (int j=i+1;j<=N-1;j++) F[j]=((arg-x[i])*F[j]-(arg-x[j])*F[i])/(x[j]-x[i]); wobei Array F die Zwischenwerte des Lagrange-Polynoms sind. Zunächst sollte F[I] gleich y i gesetzt werden. Nach der Ausführung der Schleifen ist F[N] der Wert des Lagrange-Polynoms vom Grad N am Punkt XX. Eine andere Form der Darstellung des Interpolationspolynoms sind Newtons Formeln. Seien äquidistante Interpolationsknoten; i=0,1,…,n ; - Interpolationsschritt. Newtons erste Interpolationsformel, die für die Vorwärtsinterpolation verwendet wird, lautet: Man nennt sie (endliche) Differenzen i-ter Ordnung. Sie sind wie folgt definiert: Normalisiertes Argument. Wenn Newtons Interpolationsformel in eine Taylor-Reihe übergeht. Zur „Rückwärtsinterpolation“ wird Newtons 2. Interpolationsformel verwendet: Im letzten Eintrag werden anstelle von Differenzen (sogenannte „Vorwärts“-Differenzen) „Rückwärts“-Differenzen verwendet: Bei ungleichmäßig verteilten Knotenpunkten, den sogenannten getrennte Unterschiede In diesem Fall hat das Interpolationspolynom in Newton-Form die Form Im Gegensatz zur Lagrange-Formel wird ein neues Wertepaar hinzugefügt. (x n +1, y n +1) wird hier auf die Hinzufügung eines neuen Termes reduziert. Daher kann die Anzahl der Interpolationsknoten leicht erhöht werden, ohne die gesamte Berechnung wiederholen zu müssen. Dadurch können Sie die Genauigkeit der Interpolation beurteilen. Allerdings erfordern Newtons Formeln mehr Rechenoperationen als Lagranges Formeln. Für n=1 erhalten wir die Formel für die lineare Interpolation: Für n=2 erhalten wir die Formel für die parabolische Interpolation: Bei der Interpolation von Funktionen werden algebraische Polynome höheren Grades aufgrund des erheblichen Rechenaufwands und der großen Fehler bei der Berechnung der Werte selten verwendet. In der Praxis wird am häufigsten die stückweise lineare oder stückweise parabolische Interpolation verwendet. Bei der stückweisen linearen Interpolation wird die Funktion f(x) im Intervall (i=0,1,…,n-1) durch ein gerades Liniensegment angenähert Ein Berechnungsalgorithmus, der eine stückweise lineare Interpolation implementiert, kann mit dem Operator geschrieben werden: für (int i=0;i if ((arg>=Fx[i]) && (arg<=Fx)) res=Fy[i]+(Fy-Fy[i])*(arg-Fx[i])/(Fx-Fx[i]); Mit der ersten Schleife suchen wir, wo sich der gewünschte Punkt befindet. Bei der stückweisen parabolischen Interpolation wird das Polynom unter Verwendung der drei Knotenpunkte konstruiert, die dem angegebenen Wert des Arguments am nächsten liegen. Der Berechnungsalgorithmus, der die stückweise parabolische Interpolation implementiert, kann mit dem Operator geschrieben werden: für (int i=0;i y0=Fy; Wenn i=0, existiert das Element nicht! x0=Fx; Das selbe res=y0+(y1-y0)*(arg-x0)/(x1-x0)+(1/(x2-x0))*(arg-x0)*(arg-x1)*(((y2-y1) /(x2-x1))-((y1-y0)/(x1-x0))); Der Einsatz von Interpolation ist nicht immer ratsam. Bei der Verarbeitung experimenteller Daten ist es wünschenswert, die Funktion zu glätten. Die Approximation experimenteller Abhängigkeiten mithilfe der Methode der kleinsten Quadrate basiert auf der Anforderung, den quadratischen Mittelwertfehler zu minimieren Die Koeffizienten des Approximationspolynoms werden durch die Lösung eines Systems von m+1 linearen Gleichungen, den sogenannten, ermittelt. „normale“ Gleichungen, k=0,1,…,m Neben algebraischen Polynomen werden häufig auch trigonometrische Polynome zur Approximation von Funktionen verwendet (siehe „Numerische harmonische Analyse“). Splines sind ein wirksames Mittel zur Approximation einer Funktion. Ein Spline erfordert, dass seine Werte und Ableitungen an Knotenpunkten bis zu einer bestimmten Ordnung mit der interpolierten Funktion f(x) und ihren Ableitungen übereinstimmen. Die Konstruktion von Splines erfordert jedoch in manchen Fällen einen erheblichen Rechenaufwand. Als Ergebnis der Messungen während des Experiments soll eine tabellarische Zuordnung einer bestimmten Funktion erhalten werden f(x), Ausdruck der Beziehung zwischen zwei geografischen Parametern: Natürlich können Sie eine Formel finden, die diese Abhängigkeit analytisch ausdrückt, indem Sie die Interpolationsmethode verwenden. Allerdings bedeutet die Übereinstimmung der Werte der erhaltenen analytischen Spezifikation der Funktion an den Interpolationsknoten mit den verfügbaren empirischen Daten oft nicht eine Übereinstimmung des Verhaltens der ursprünglichen und interpolierenden Funktion über das gesamte Beobachtungsintervall. Darüber hinaus wird die tabellarische Abhängigkeit geografischer Indikatoren immer durch Messungen mit verschiedenen Instrumenten gewonnen, die einen gewissen und nicht immer ausreichend kleinen Messfehler aufweisen. Die Forderung nach einer exakten Übereinstimmung der Werte der Näherungs- und Näherungsfunktionen an den Knoten ist umso ungerechtfertigter, wenn die Werte der Funktion f(x), Bei den durch Messungen erhaltenen Werten handelt es sich um Näherungswerte. Das Problem, eine Funktion einer Variablen von Anfang an zu approximieren, berücksichtigt notwendigerweise das Verhalten der ursprünglichen Funktion über das gesamte Beobachtungsintervall. Die Problemstellung lautet wie folgt. Funktion y= f(x) gegeben durch Tabelle (1). Es ist notwendig, eine Funktion eines bestimmten Typs zu finden: Das ist an Punkten x 1 , x 2 , …, x n nimmt Werte an, die den Tabellenwerten so nahe wie möglich kommen y 1, y 2, …, y n. In der Praxis wird die Art der Näherungsfunktion am häufigsten durch Vergleich der Form des näherungsweise konstruierten Graphen der Funktion bestimmt y= f(x) mit Graphen von Funktionen, die dem Forscher bekannt sind und analytisch spezifiziert werden (meistens Elementarfunktionen, die einfach aussehen). Gemäß Tabelle (1) wird nämlich ein Streudiagramm erstellt f(x), Anschließend wird eine glatte Kurve gezeichnet, die die Art der Position der Punkte so gut wie möglich widerspiegelt. Basierend auf der so erhaltenen Kurve wird auf qualitativer Ebene die Form der Näherungsfunktion festgelegt. Betrachten Sie Abbildung 6. Abbildung 6 zeigt drei Situationen: Es ist zu beachten, dass eine strikte funktionale Abhängigkeit für eine Tabelle mit Ausgangsdaten selten beobachtet wird, da jede der darin enthaltenen Größen von vielen Zufallsfaktoren abhängen kann. Formel (2) (wird jedoch empirische Formel oder Regressionsgleichung genannt bei An X) ist interessant, weil Sie damit die Werte der Funktion finden können F für nicht tabellarische Werte X, „Glättung“ der Ergebnisse von Mengenmessungen bei, d.h. im gesamten Spektrum der Veränderungen X. Die Berechtigung dieses Ansatzes wird letztlich durch den praktischen Nutzen der resultierenden Formel bestimmt. Durch die bestehende „Wolke“ von Punkten kann man immer versuchen, eine Linie eines etablierten Typs zu zeichnen, die in gewisser Weise die beste unter allen Linien eines bestimmten Typs ist, also den Beobachtungspunkten in ihrem „am nächsten“ liegt Gesamtheit. Dazu definieren wir zunächst das Konzept der Nähe einer Linie zu einer bestimmten Menge von Punkten auf der Ebene. Die Maße dieser Nähe können variieren. Allerdings muss jedes vernünftige Maß offensichtlich auf den Abstand zwischen den Beobachtungspunkten und der betreffenden Linie (durch die Gleichung gegeben) bezogen werden y=F(x)).
Nehmen wir an, dass die Näherungsfunktion F(x) an Punkten x 1, x 2, ..., x n Gegenstand j 1 , j 2 , ..., j N. Als Näherungskriterium wird häufig die minimale Summe der quadrierten Differenzen zwischen Beobachtungen der abhängigen Variablen verwendet y i und theoretische Werte, die mithilfe der Regressionsgleichung berechnet werden j ich. Hier wird angenommen, dass y i Und x i- bekannte Beobachtungsdaten und F- Gleichung einer Regressionsgeraden mit unbekannten Parametern (Formeln zu deren Berechnung werden unten angegeben). Man nennt eine Methode zur Schätzung von Parametern einer Näherungsfunktion, die die Summe der quadrierten Abweichungen der Beobachtungen der abhängigen Variablen von den Werten der gewünschten Funktion minimiert Methode des Mindestens Quadrate (LS) oder Methode der kleinsten Quadrate (LS). Also das Funktionsnäherungsproblem F lässt sich nun wie folgt formulieren: für die Funktion F, gegeben durch Tabelle (1), finden Sie die Funktion F einen bestimmten Typ, so dass die Quadratsumme Ф am kleinsten ist. Betrachten wir die Methode zum Finden einer Näherungsfunktion in allgemeiner Form am Beispiel einer Näherungsfunktion mit drei Parametern: Lassen F(x i , a, b, c) = y i , i=1, 2, ..., n. Summe der quadrierten Differenzen der entsprechenden Werte F Und F wird aussehen wie: Diese Summe ist eine Funktion von Ф (a, b, c) drei Variablen (Parameter a, b Und C). Die Aufgabe besteht darin, das Minimum zu finden. Wir verwenden die notwendige Bedingung für ein Extremum: Wir erhalten ein System zur Bestimmung der unbekannten Parameter a, b, c. Nachdem wir dieses System aus drei Gleichungen mit drei Unbekannten bezüglich der Parameter gelöst haben a, b, c, Wir erhalten die spezifische Form der gewünschten Funktion F(x, a, b, c). Wie aus dem betrachteten Beispiel hervorgeht, führt eine Änderung der Anzahl der Parameter nicht zu einer Verzerrung des Wesens des Ansatzes selbst, sondern äußert sich lediglich in einer Änderung der Anzahl der Gleichungen im System (5). Es ist natürlich zu erwarten, dass die Werte der gefundenen Funktion F(x, a, b, c) an Punkten x 1, x 2, ..., x n, weichen von den Tabellenwerten ab y 1 , y 2 , ..., y n. Differenzwerte y i -F(x i ,a, b, c)=e i (i=1, 2, ..., n) werden Abweichungen von Messwerten genannt j aus denen, die nach Formel (3) berechnet wurden. Für die gefundene empirische Formel (2) gemäß der Originaltabelle (1) lässt sich also finden die Summe der quadratischen Abweichungen, die gemäß der Methode der kleinsten Quadrate für einen bestimmten Typ einer Näherungsfunktion (und die gefundenen Parameterwerte) am kleinsten sein sollten. Von zwei verschiedenen Näherungen derselben Tabellenfunktion nach der Methode der kleinsten Quadrate sollte diejenige als beste angesehen werden, bei der die Summe (4) den kleinsten Wert hat. In der experimentellen Praxis als Näherungsfunktionen abhängig von der Art des Streudiagramms F Häufig werden Näherungsfunktionen mit zwei Parametern verwendet: Wenn der Typ der Näherungsfunktion festgelegt ist, beschränkt sich die Aufgabe natürlich nur darauf, die Werte der Parameter zu ermitteln. Betrachten wir die häufigsten empirischen Abhängigkeiten in der praktischen Forschung. 3.3.1. Lineare Funktion (lineare Regression). Der Ausgangspunkt der Abhängigkeitsanalyse ist normalerweise die Schätzung der linearen Abhängigkeit der Variablen. Dabei ist jedoch zu berücksichtigen, dass es zwar immer die „beste“ Gerade nach der Methode der kleinsten Quadrate gibt, diese aber nicht immer gut genug ist. Wenn in Wirklichkeit Sucht y=f(x) quadratisch ist, kann keine lineare Funktion sie ausreichend beschreiben, obwohl es unter all diesen Funktionen sicherlich eine „beste“ geben wird. Wenn die Werte X Und beiüberhaupt nicht zusammenhängen, können wir auch immer die „beste“ lineare Funktion finden y=ax+b für einen gegebenen Satz von Beobachtungen, in diesem Fall jedoch spezifische Werte A Und B werden nur durch zufällige Abweichungen der Variablen bestimmt und variieren selbst stark für verschiedene Stichproben derselben Grundgesamtheit. Betrachten wir nun das Problem der Schätzung linearer Regressionskoeffizienten formaler. Nehmen wir an, dass der Zusammenhang zwischen X Und j ist linear und wir suchen nach der gewünschten Näherungsfunktion in der Form: Finden wir partielle Ableitungen nach den Parametern: Ersetzen wir die erhaltenen Beziehungen in ein System der Form (5): oder jede Gleichung durch n dividieren: Führen wir die folgende Notation ein: Dann sieht das letzte System so aus: Die Koeffizienten dieses Systems M x , M y , M xy , M x 2- Zahlen, die in jedem spezifischen Näherungsproblem leicht mit den Formeln (7) berechnet werden können, wobei x i, y i- Werte aus Tabelle (1). Nachdem wir System (8) gelöst haben, erhalten wir die Parameterwerte A Und B und damit die spezifische Form der linearen Funktion (6). Eine notwendige Voraussetzung für die Wahl einer linearen Funktion als gewünschte empirische Formel ist die Beziehung: 3.3.2. Quadratische Funktion (quadratische Regression). Wir suchen nach einer Näherungsfunktion in Form eines quadratischen Trinoms: Partielle Ableitungen finden: Erstellen wir ein System der Form (5): Nach einfachen Transformationen erhalten wir ein System aus drei linearen Gleichungen mit drei Unbekannten a, b, c. Die Koeffizienten des Systems werden wie bei einer linearen Funktion nur durch die bekannten Daten aus Tabelle (1) ausgedrückt: Hier verwenden wir die Notation (7) sowie Die Lösung von System (10) ergibt den Wert der Parameter a, b Und Mit für die Näherungsfunktion (9). Die quadratische Regression wird angewendet, wenn alle Ausdrücke der Form y 2 -2y 1 + y 0 , y 3 -2 y 2 + y 1 , y 4 -2 y 3 + y 2 usw. unterscheiden sich kaum voneinander.
3.3.3. Potenzfunktion (geometrische Regression). Finden wir nun die Näherungsfunktion in der Form: Unter der Annahme, dass in der Originaltabelle (1) die Werte des Arguments und die Funktionswerte positiv sind, nehmen wir den Logarithmus der Gleichheit (11) unter der Bedingung a>0: Da die Funktion F ist eine Näherung für die Funktion F, Funktion lnF wird eine Näherung für die Funktion sein lnf. Lassen Sie uns eine neue Variable einführen u=lnx; dann, wie aus (12) folgt, lnF wird eine Funktion von sein u:
Ф(u). Bezeichnen wir Nun hat Gleichheit (12) die Form: diese. Das Problem reduzierte sich darauf, eine Näherungsfunktion in Form einer linearen zu finden. Um in der Praxis die gewünschte Näherungsfunktion in Form einer Potenzfunktion zu finden (unter den oben getroffenen Annahmen), ist Folgendes erforderlich: 1. Erstellen Sie anhand dieser Tabelle (1) eine neue Tabelle und logarithmieren Sie die Werte X Und j in der Quelltabelle; 2. Verwenden Sie die neue Tabelle, um die Parameter zu finden A Und IN Näherungsfunktion der Form (14); 3. Ermitteln Sie mithilfe der Notation (13) die Werte der Parameter A Und M und ersetzen Sie sie in Ausdruck (11). Eine notwendige Voraussetzung für die Wahl einer Potenzfunktion als gewünschte empirische Formel ist die Beziehung: 3.3.4. Exponentialfunktion .
Die ursprüngliche Tabelle (1) soll so beschaffen sein, dass es ratsam ist, nach der Näherungsfunktion in Form einer Exponentialfunktion zu suchen: Nehmen wir den Logarithmus der Gleichheit (15): Unter Verwendung der Notation (13) schreiben wir (16) in der Form um: Um die Näherungsfunktion in der Form (15) zu finden, ist es daher notwendig, die Funktionswerte in der Originaltabelle (1) zu logarithmieren und unter Berücksichtigung dieser zusammen mit den Originalwerten des Arguments eine Näherungsfunktion zu konstruieren des Formulars (17) für die neue Tabelle. Danach müssen gemäß Notation (13) noch die Werte der gesuchten Parameter ermittelt werden A Und B und setze sie in Formel (15) ein. Eine notwendige Voraussetzung für die Wahl einer Exponentialfunktion als gewünschte empirische Formel ist die Beziehung: 3.3.5. Gebrochene lineare Funktion. Wir suchen nach einer Näherungsfunktion in der Form: Wir schreiben Gleichheit (18) wie folgt um: Aus der letzten Gleichung folgt, dass die Parameterwerte ermittelt werden müssen A Und B Für eine bestimmte Tabelle (1) müssen Sie eine neue Tabelle erstellen, in der die Argumentwerte gleich bleiben und die Funktionswerte durch inverse Zahlen ersetzt werden. Anschließend müssen Sie für die resultierende Tabelle eine Näherung finden Funktion der Form Axt+b. Parameterwerte gefunden A Und B in Formel (18) einsetzen. Eine notwendige Voraussetzung für die Wahl einer gebrochenen linearen Funktion als gewünschte empirische Formel ist die Beziehung: 3.3.6. Logarithmische Funktion. Die Näherungsfunktion soll die Form haben: Es ist leicht zu erkennen, dass es ausreicht, eine Substitution vorzunehmen, um zu einer linearen Funktion zu gelangen lnx=u. Daraus folgt, die Werte zu finden A Und B Sie müssen die Werte des Arguments in der Originaltabelle (1) logarithmieren und unter Berücksichtigung der erhaltenen Werte in Verbindung mit den Originalwerten der Funktion eine Näherungsfunktion in Form einer linearen für finden die so erhaltene neue Tabelle. Chancen A Und B Ersetzen Sie die gefundene Funktion in Formel (19). Eine notwendige Voraussetzung für die Wahl einer logarithmischen Funktion als gewünschte empirische Formel ist die Beziehung: 3.3.7. Hyperbel. Wenn ein aus Tabelle (1) erstelltes Streudiagramm einen Zweig einer Hyperbel ergibt, kann die Näherungsfunktion in der Form gesucht werden.
1
| | | | | | | | | | | |
X
x 1
x 2
…
x n
f(x)
Jahr 1
um 2
…
y n
![]()
![]() (3)
(3)![]()
 (5)
(5)
![]()



 (7)
(7) (8)
(8)![]()

 (10)
(10)![]() (11)
(11)![]() (16)
(16)![]() (17)
(17) .
.
![]() (18)
(18)
 .
.![]() .
.
 Die Geschichte der Piloten, die Hiroshima und Nagasaki bombardierten
Die Geschichte der Piloten, die Hiroshima und Nagasaki bombardierten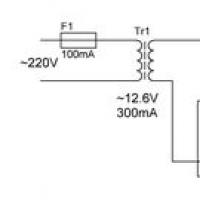 Reibungsloses Laden der Kapazität: Was soll ich wählen?
Reibungsloses Laden der Kapazität: Was soll ich wählen?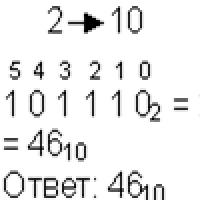 Kleine Fakultät für Mathematik
Kleine Fakultät für Mathematik „Warum träumst du im Traum von einem Reigentanz?
„Warum träumst du im Traum von einem Reigentanz? Warum träumen Sie von der Kirche im Inneren: Interpretation der Traumbedeutung gemäß verschiedenen Traumbüchern für Männer und Frauen
Warum träumen Sie von der Kirche im Inneren: Interpretation der Traumbedeutung gemäß verschiedenen Traumbüchern für Männer und Frauen Traumdeutung von Persimone, warum träumst du von Persimone in einem Traum, um Persimone in einem Traum zu sehen, warum
Traumdeutung von Persimone, warum träumst du von Persimone in einem Traum, um Persimone in einem Traum zu sehen, warum Verzauberte Seele Bedeutung karmischer Zahlen
Verzauberte Seele Bedeutung karmischer Zahlen