Mis on numbrisüsteemid? Väike matemaatikateaduskond. Kümnendsüsteemi murdosa teisendamine mis tahes teiseks
Märge on meetod numbri kirjutamiseks, kasutades kindlaksmääratud erimärkide (numbrite) komplekti.
Märge:
- annab arvude (täisarvude ja/või reaalarvude) hulga esituse;
- annab igale numbrile kordumatu esituse (või vähemalt standardse esituse);
- kuvab arvu algebralise ja aritmeetilise struktuuri.
Arvu kirjutamist mingis numbrisüsteemis nimetatakse numbrikood.
Numbrinäidikul kutsutakse välja eraldi positsioon tühjenemine, mis tähendab, et positsiooni number on järgu number.
Kutsutakse numbrite arvu numbris biti sügavus ja langeb kokku selle pikkusega.
Numbrisüsteemid jagunevad positsiooniline Ja mittepositsiooniline. Positsiooninumbrisüsteemid on jagatud
peal homogeenne Ja segatud.
kaheksandarvusüsteem, kuueteistkümnendsüsteem ja muud arvusüsteemid.
Numbrisüsteemide tõlkimine. Arvu saab teisendada ühest numbrisüsteemist teise.
Erinevate arvusüsteemide arvude vastavustabel.
On positsioonilisi ja mittepositsioonilisi arvusüsteeme.
Mittepositsioonilistes arvusüsteemides numbri kaal (st selle panus numbri väärtusesse) ei sõltu tema positsioonist numbrit kirjutades. Seega on Rooma numbrisüsteemis arvus XXXII (kolmkümmend kaks) numbri X kaal mis tahes asendis lihtsalt kümme.
Positsioonilistes arvusüsteemides iga numbri kaal varieerub olenevalt selle asukohast (asendist) numbrit tähistavate numbrite jadas. Näiteks numbris 757.7 tähendab esimene seitse 7 sadu, teine - 7 ühikut ja kolmas - 7 kümnendikku ühikust.
Arvu 757,7 märge tähendab väljendi lühendatud tähistust
700 + 50 + 7 + 0,7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757,7.
Iga positsioonilist arvusüsteemi iseloomustab selle alus.
Süsteemi aluseks võib võtta mis tahes naturaalarvu – kaks, kolm, neli jne. Seega võimalikud lugematud asukohasüsteemid: kahend-, kolme-, kvaternaarne jne. Arvude kirjutamine igasse numbrisüsteemi alusega q tähendab stenogrammi väljendit
a n-1 q n-1 + a n-2 q n-2 + ... +a 1 q 1 + a 0 q 0 + a -1 q -1 + ... + a -m q -m ,
Kus a i - numbrisüsteemi numbrid; n Ja m - vastavalt täis- ja murdarvude arv. Näiteks:
Milliseid numbrisüsteeme kasutavad spetsialistid arvutiga suhtlemiseks?
Lisaks kümnendarvule kasutatakse laialdaselt süsteeme, mille alus on täisarvuline aste 2, nimelt:
binaarne(kasutatakse numbreid 0, 1);
kaheksand(kasutatakse numbreid 0, 1, ..., 7);
kuueteistkümnendsüsteem(esimeste täisarvude puhul nullist üheksani kasutatakse numbreid 0, 1, ..., 9 ja järgmiste numbrite jaoks - kümnest viieteistkümneni - sümboleid A, B, C, D, E, F numbritena).
Nendes numbrisüsteemides on kasulik meeles pidada kahe esimese kümne täisarvu tähistust:
|
|
|
Kõigist numbrisüsteemidest eriti lihtne ning seetõttu Kahendarvusüsteem on huvitav arvutite tehniliseks rakendamiseks.
Mis on numbrisüsteem?
Mis on numbrisüsteem? Arvusüsteem on tehnikate ja reeglite kogum, mille järgi arve kirjutatakse ja loetakse.
On positsioonilisi ja mittepositsioonilisi arvusüsteeme.
Mittepositsioonilistes arvusüsteemides ei sõltu numbri kaal (st selle panus arvu väärtusesse) selle asukohast arvu tähistuses. Seega on Rooma numbrisüsteemis arvus XXXII (kolmkümmend kaks) numbri X kaal mis tahes asendis lihtsalt kümme.
Positsioonilistes numbrisüsteemides varieerub iga numbri kaal sõltuvalt selle asukohast (asendist) numbrit tähistavate numbrite jadas. Näiteks numbris 757.7 tähendab esimene seitse 7 sadu, teine - 7 ühikut ja kolmas - 7 kümnendikku ühikust.
Arvu 757.7 märge tähendab väljendi lühendatud tähistust:
Iga positsiooninumbrisüsteemi iseloomustab selle alus.
Positsioonilise numbrisüsteemi alus on erinevate numbrite arv, mida kasutatakse arvude esitamiseks antud numbrisüsteemis.
Süsteemi aluseks võib võtta mis tahes naturaalarvu – kaks, kolm, neli jne. Järelikult on võimalik lõpmatu arv positsioonisüsteeme: kahend-, kolme-, kvaternaarsed jne.
Kuidas genereeritakse täisarve positsioonilistes arvusüsteemides?
Igas numbrisüsteemis järjestatakse numbrid nende tähenduse järgi: 1 on suurem kui 0, 2 on suurem kui 1 jne.
Numbri ülendamine tähendab selle asendamist järgmise numbriga.
Arvu 1 edenemine tähendab selle asendamist 2-ga, numbri 2 edasiarendamine tähendab selle asendamist 3-ga jne. Esinumbri (näiteks kümnendsüsteemis arvu 9) esiletõstmine tähendab selle asendamist 0-ga. Kahendsüsteemis, mis kasutab ainult kahte numbrit - 0 ja 1, tähendab 0 esiletõstmine selle asendamist 1-ga ja edendamist. 1 tähendab selle asendamist 0-ga.
Mistahes täisarvule järgneva täisarvu moodustamiseks tuleb arvu parempoolseimat numbrit edasi lükata; kui mõni number muutub pärast edutamist nulliks, peate tõstma sellest vasakul asuva numbri.
Seda reeglit rakendades paneme kirja esimesed kümme täisarvu
· kahendsüsteemis: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
· kolmekomponendilises süsteemis: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
· viiekordses süsteemis: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
· kaheksandsüsteemis: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Lisaks kümnendarvule kasutatakse laialdaselt süsteeme, mille alus on täisarvuline aste 2, nimelt:
| Binaarsüsteem | Kvaternaarsüsteem | Oktaalne süsteem | Kümnendsüsteem | Kuueteistkümnendsüsteem |
| 1 | 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 | 3 |
| 100 | 10 | 4 | 4 | 4 |
| 101 | 11 | 5 | 5 | 5 |
| 110 | 12 | 6 | 6 | 6 |
| 111 | 13 | 7 | 7 | 7 |
| 1000 | 20 | 10 | 8 | 8 |
| 1001 | 21 | 11 | 9 | 9 |
| 1010 | 22 | 12 | 10 | A |
| 1011 | 23 | 13 | 11 | B |
| 1100 | 30 | 14 | 12 | C |
| 1101 | 31 | 15 | 13 | D |
| 1110 | 32 | 16 | 14 | E |
| 1111 | 33 | 17 | 15 | F |
| 10000 | 40 | 20 | 16 | 10 |
Inimesed eelistavad kümnendsüsteemi ilmselt seetõttu, et nad on iidsetest aegadest lugenud sõrmedel ning inimestel on kümme sõrme ja varvast. Inimesed ei kasuta alati ja mitte igal pool kümnendarvude süsteemi. Näiteks Hiinas kasutati pikka aega viiekohalist numbrisüsteemi.
Ja arvutid kasutavad kahendsüsteemi, kuna sellel on teiste süsteemide ees mitmeid eeliseid:
· selle elluviimiseks vajame tehnilisi seadmeid, millel on kaks stabiilset olekut (vool on olemas - voolu puudub, magnetiseeritud - pole magnetiseeritud jne), mitte näiteks kümnega, nagu kümnendkohana;
· teabe esitamine ainult kahe oleku kaudu on usaldusväärne ja mürakindel;
· on võimalik kasutada Boole'i algebra aparatuuri teabe loogiliste teisenduste läbiviimiseks;
· Binaararitmeetika on palju lihtsam kui kümnendaritmeetika.
Kahendsüsteemi puuduseks on numbrite salvestamiseks vajalike numbrite arvu kiire kasv.
Miks kasutavad arvutid ka kaheksand- ja kuueteistkümnendsüsteemi arvusüsteeme?
Arvutite jaoks mugav kahendsüsteem on oma mahukuse ja ebatavalise tähistuse tõttu inimestele ebamugav.
Arvude teisendamise kümnendsüsteemist kahendsüsteemi ja vastupidi teostab masin. Arvuti professionaalseks kasutamiseks tuleb aga õppida mõistma sõna masin. Seetõttu töötati välja kaheksand- ja kuueteistkümnendsüsteemid.
Nendes süsteemides on numbreid peaaegu sama lihtne lugeda kui kümnendarvu; nende jaoks on vaja vastavalt kolm (kaheksand) ja neli (kuueteistkümnend) korda vähem numbreid kui kahendsüsteemis (numbrid 8 ja 16 on ju vastavalt arvu kolmas ja neljas aste 2) .
Arvude teisendamine ühest numbrisüsteemist teise
Positsioonisüsteemis kasutatav erinevate numbrite arv p määrab numbrisüsteemi nime ja seda nimetatakse numbrisüsteemi aluseks - “p”. Mis tahes arvu N positsiooninumbrisüsteemis, mille alus on p, võib esitada polünoomina aluses p:
N = a n p n +a n-1 p n-1 + ... +a 1 p+a 0 +a -1 p -1 +a -2 p -2 + ... (1.1)
siin N on arv, a j on koefitsiendid (arvu numbrid), p on arvusüsteemi alus (p>1). Arve on tavaks esitada numbrite jadana:
N = a n a n -1 ... a 1 a 0 . a -1 a -2 ...
Arvude teisendamine kümnendsüsteemiks toimub astmerea koostamisel süsteemi alusega (vt valem 1.1), millest arv teisendatakse. Seejärel arvutatakse summa väärtus.
|
|
|
|
Täisarvulised kümnendarvud teisendatakse kümnendsüsteemita arvusüsteemiks, jagades kümnendarvu järjestikku selle süsteemi alusega, milleks see teisendatakse, kuni saadakse selle aluse jagatis. Arv uues süsteemis kirjutatakse jagamisjääkidena, alustades viimasest.
Näide: teisendame arvu 75 kümnendsüsteemist kahend-, kaheksand- ja kuueteistkümnendsüsteemiks:

Vastus: 75 10 = 1 001 011 2 = 113 8 = 4B 16.
Õigete murdude teisendamine kümnendarvusüsteemist mittekoma arvusüsteemi. Tavalise kümnendmurru teisendamiseks teise süsteemi, tuleb see murd järjestikku korrutada selle süsteemi baasiga, milleks see teisendatakse. Sel juhul korrutatakse ainult murdosasid. Murrud kirjutatakse uues süsteemis toodete tervete osadena, alustades esimesest.
Näide. Teisendame kümnendsüsteemi arvu 0,36 kahend-, kaheksand- ja kuueteistkümnendsüsteemiks:

Ebakorrapärase kümnendmurru teisendamiseks mittekomapõhjaga arvusüsteemiks tuleb eraldi teisendada terve osa ja murdosa eraldi. Tõlgi 23.125 10 2 s.s.
Arvusüsteeme nimetatakse mitmekordseteks, kui kehtib järgmine seos: S = R N , kus S, R on arvusüsteemide alused, N on kordsuse aste (täisarv: 2, 3 ...).
Arvu teisendamiseks arvusüsteemist R selle mitmearvuliseks süsteemiks S toimige järgmiselt: liikudes punktist vasakule ja paremale, jagatakse arv N-kohalisteks rühmadeks, täiendades kõige vasakpoolseimat ja parempoolseimat rühma nullidega, kui vajalik. Seejärel asendatakse rühm vastava numbriga S-numbrisüsteemist.
| Tõlgi 1101111001.1101 2 "8" s.s. | Tõlgi 11111111011.100111 2 "16" s.c. |
Arvu teisendamiseks arvusüsteemist S selle mitmekordseks arvusüsteemiks R piisab, kui asendada selle arvu iga number vastava numbriga numbrisüsteemist R, kusjuures tähtsusetud nullid kõrges (00512) ja madalas (15,124000) numbrid jäetakse kõrvale.
| Tõlgi 305.4 8 "2" s.s. | Tõlgi 7B2.E 16 "2" s.s. |
|
|
Kui teil on vaja teisendada arvusüsteemist S R-ks, eeldusel, et need pole kordsed, peate proovima valida sellise arvusüsteemi K, et: S = K N ja R = K N .
Tõlgi 175.24 8 "16" s.s.
Tulemus: 175,24 8 = 7D,5 16.
Kui arvusüsteemi K ei leita, tuleks tõlge sooritada kasutades vahelülina kümnendarvusüsteemi.
Näited kõige selle kohta
Kaheksandik- ja kuueteistkümnendarvude teisendamine kahendsüsteemiks on väga lihtne: piisab, kui asendada iga number samaväärse binaartriaadiga (kolm numbrit) või tetraadiga (neli numbrit).
Näiteks:
Arvu binaararvust kaheksand- või kuueteistkümnendarvuks teisendamiseks peate selle koma vasakule ja paremale poolde jagama kolmkõladeks (oktaali jaoks) või tetraadideks (kuueteistkümnendsüsteemi jaoks) ja asendama iga sellise rühma vastava kaheksandkoha (kuueteistkümnendsüsteemi) numbriga. . Näiteks:

Liitmine erinevates numbrisüsteemides
Liitmistabeleid on loendusreegli abil lihtne luua.






Lahutamine erinevates arvusüsteemides

Korrutamine erinevates arvusüsteemides
Mitmekohaliste arvude korrutamisel erinevates positsioonilistes arvusüsteemides saab kasutada tavalist tulbas olevate arvude korrutamise algoritmi, kuid ühekohaliste arvude korrutamise ja liitmise tulemused tuleb laenata süsteemile vastavatest korrutamis- ja liitmistabelitest. küsimus.



Jagamine erinevates numbrisüsteemides
Jagamine mis tahes positsioonilises numbrisüsteemis toimub samade reeglite järgi nagu kümnendsüsteemis nurga järgi jagamine. Kahendsüsteemis on jagamine eriti lihtne, kuna jagatise järgmine number saab olla ainult null või üks.
Korrutage uue arvusüsteemi alusega, kuni uus murd sisaldab vajaliku arvu numbreid, mille määrab murru esitamise nõutav täpsus. Korralik murd uues arvusüsteemis kirjutatakse järjestikuse korrutise tulemusel saadud korrutise täisarvu osadest ja esimene täisarv on uue murru kõrgeim number. Võtame näite...

Esitused neis on üsna suured arvud, kuna see toob kaasa äärmiselt tülika numbrite märkimise või nõuab väga suurt numbrite tähestikku. Arvutid kasutavad ainult positsioonilisi arvusüsteeme, milles tähestiku iga numbri kvantitatiivne ekvivalent sõltub mitte ainult selle numbri tüübist, vaid ka selle asukohast numbri märkimisel. Positsiooninumbrisüsteemid...





Jadad 0 ja 1. Näiteks mittenegatiivne täisarv A2=T 111100002 salvestatakse lahtrisse järgmiselt: 1 1 1 1 0 0 0 0 See tähendab, et saame kahendkoodi kirjutada kõik arvud vahemikus 0 kuni 255 numbrisüsteem 1 mälulahtris. 2.2 Arvude esitamine arvutis Arvuti täisarvud salvestatakse mälurakkudesse, sel juhul vastab igale mälulahtri numbrile...
Numbrite kujutamine kirjalike sümbolite abil.
Märge:
- annab arvude hulga (täisarvude ja/või reaalarvude) esitusi;
- annab igale numbrile kordumatu esituse (või vähemalt standardse esituse);
- peegeldab arvude algebralist ja aritmeetilist struktuuri.
Numbrisüsteemid jagunevad positsiooniline, mittepositsiooniline Ja segatud.
Positsiooninumbrisüsteemid
Positsioonilistes numbrisüsteemides on samal numbrimärgil (numbril) arvu tähistuses erinev tähendus olenevalt kohast (numbrist), kus see asub. Positsioonilise numeratsiooni leiutamine, mis põhineb numbrite kohatähendusel, on omistatud sumeritele ja babüloonlastele; Sellise numeratsiooni töötasid välja hindud ja sellel olid hindamatud tagajärjed inimtsivilisatsiooni ajaloos. Selliste süsteemide hulka kuulub kaasaegne kümnendarvusüsteem, mille tekkimist seostatakse sõrmedel loendamisega. See ilmus keskaegses Euroopas Itaalia kaupmeeste kaudu, kes omakorda laenasid selle moslemitelt.
Positsiooniline numbrisüsteem viitab tavaliselt -rikkale arvusüsteemile, mis määratakse täisarvuga, mida nimetatakse alus numbrisüsteemid. Märgita täisarv -aararvude süsteemis on esitatud arvu lõpliku lineaarse kombinatsioonina:
, kus nimetatakse täisarve arvudes, mis rahuldab ebavõrdsust.Iga sellise tähise kraadi nimetatakse auastme kaaluks. Numbrite ja neile vastavate numbrite staaž määratakse näitaja (kohanumbri) väärtusega. Tavaliselt jäetakse nullist erineva numbri puhul vasakpoolsed nullid välja.
Kui lahknevusi pole (näiteks kui kõik numbrid on esitatud kordumatute kirjalike märkide kujul), kirjutatakse number selle tähtnumbriliste numbrite jadana, mis on loetletud numbrite järjekoha kahanevas järjekorras vasakult paremale:
Näiteks number sada kolm kümnendarvusüsteemis esitatud järgmiselt:
Praegu kasutatavad asukohasüsteemid on järgmised:
Positsioonisüsteemides on nii, et mida suurem on süsteemi alus, seda vähem on numbri kirjutamisel vaja numbreid (st kirjutatud numbreid).
Seganumbrisüsteemid
Seganumbrite süsteem on -rikka arvusüsteemi üldistus ja viitab sageli ka positsioonilistele arvusüsteemidele. Segaarvusüsteemi aluseks on kasvav numbrijada ja iga arv selles on kujutatud lineaarse kombinatsioonina:
, kus koefitsiente nimetatakse nagu varem arvudes, kehtivad mõned piirangud.Arvu kirjutamine segaarvusüsteemis on selle numbrite loetlemine indeksi kahanevas järjekorras, alustades esimesest nullist erineva ühega.
Sõltuvalt tüübist funktsioonina võivad segaarvusüsteemid olla astmelised, eksponentsiaalsed jne. Kui mõne jaoks langeb segaarvusüsteem kokku eksponentsiaal-rikaste arvude süsteemiga.
Kõige kuulsam näide segaarvusüsteemist on aja esitamine päevade, tundide, minutite ja sekundite arvuna. Sel juhul vastab väärtus "päevad, tunnid, minutid, sekundid" sekundite väärtusele.
Faktoriaalne arvusüsteem
IN faktoriaalarvude süsteem alused on faktoriaalide jada ja iga naturaalarv on esitatud järgmiselt:
, Kus.Faktoriaalarvude süsteemi kasutatakse siis, kui permutatsioonide dekodeerimine inversioonide loendite järgi: omades permutatsiooni numbrit, saad selle reprodutseerida järgmiselt: arvust ühe võrra väiksem arv (numeratsioon algab nullist) kirjutatakse faktoriaalarvude süsteemi ja arvu koefitsient i! tähistab elemendi i+1 inversioonide arvu komplektis, milles permutatsioonid tehakse (elementide arv, mis on väiksemad kui i+1, kuid asuvad soovitud permutatsioonis sellest paremal)
Näide: kaaluge 5 elemendist koosnevat permutatsioonide komplekti, kokku on 5! = 120 (alates permutatsiooni numbrist 0 - (1,2,3,4,5) kuni permutatsiooni numbrini 119 - (5,4,3,2,1)), leiame 101. permutatsiooni: 100 = 4!* 4 + 3!*0 + 2!*2 + 1!*0 = 96 + 4; olgu ti arvu i koefitsient!, siis t4 = 4, t3 = 0, t2 = 2, t1 = 0, siis: elementide arv, mis on väiksem kui 5, kuid asuvad paremal, on 4; elementide arv alla 4, kuid asub paremal on 0; elementide arv on väiksem kui 3, kuid mis asuvad paremal, on 2; elementide arv, mis on väiksem kui 2, kuid asuvad paremal, on 0 (permutatsiooni viimane element “panetakse” ainsasse allesjäänud kohta) - seega näeb 101. permutatsioon välja selline: (5,3,1,2 ,4) Seda meetodit saab kontrollida, loendades otseselt iga permutatsiooni elemendi inversioonid.
Fibonacci numbrisüsteem Fibonacci numbrite põhjal. Iga naturaalarv on esitatud kujul:
, kus on Fibonacci arvud ja koefitsientidel on lõplik arv ühendeid ja kahte ühte järjestikust pole.Mittepositsioonilised arvusüsteemid
Mittepositsioonilistes arvusüsteemides ei sõltu number, mida number tähistab, selle asukohast arvus. Sel juhul saab süsteem kehtestada piiranguid näiteks numbrite asukohale, et need oleksid järjestatud kahanevas järjekorras.
Binoomarvude süsteem
Esitamine binoomkoefitsientide abil
, Kus.Jääkklassi süsteem (RSS)
Arvu esitamine jäägiklassi süsteemis põhineb jäägi mõistel ja Hiina jäägiteoreemil. RNS määratakse suhteliselt algväärtuste hulgaga moodulid korrutisega nii, et iga täisarv segmendist on seotud jääkide hulgaga, kus
…Samal ajal tagab Hiina jäägiteoreem intervallist arvude esituse kordumatuse.
RNS-is sooritatakse aritmeetilised toimingud (liitmine, lahutamine, korrutamine, jagamine) komponentide kaupa, kui on teada, et tulemus on täisarv ja asub samuti .
RNS-i miinusteks on võime esitada vaid piiratud arvu numbreid, aga ka tõhusate algoritmide puudumine RNS-is esitatud arvude võrdlemiseks. Võrdlus viiakse tavaliselt läbi argumentide tõlkimise teel RNS-ist segaradiksi numbrisüsteemi.
Sterni-Brocoti numbrisüsteem- positiivsete ratsionaalarvude kirjutamise viis, mis põhineb Sterni-Brocoti puul.
Erinevate rahvaste numbrisüsteemid
Ühikute numbrite süsteem
Ilmselt kronoloogiliselt iga rahva loendamist valdava rahva esimene numbrisüsteem. Naturaalarvu esitatakse sama märgi (kriips või punkt) kordamisega. Näiteks numbri 26 kujutamiseks tuleb tõmmata 26 joont (või teha luule, kivile vms 26 sälku). Seejärel rühmitatakse need märgid suurte arvude tajumise mugavuse huvides kolme või viie kaupa. Siis hakkavad võrdsed mahulised märgirühmad asenduma mõne uue märgiga – nii tekivad tulevikunumbrite prototüübid.
Vana-Egiptuse numbrisüsteem
Babüloonia numbrisüsteem
Tähestikulised numbrisüsteemid
Tähestikulisi numbrisüsteeme kasutasid muistsed armeenlased, grusiinid, kreeklased (iooniline numbrisüsteem), araablased (abjadia), juudid (vt gematria) ja teised Lähis-Ida rahvad. Slaavi liturgilistes raamatutes tõlgiti kreeka tähestiku süsteem kirillitsa tähtedesse.
Juudi numbrisüsteem
Kreeka numbrisüsteem
Rooma numbrite süsteem
Peaaegu mittepositsioonilise numbrisüsteemi kanooniline näide on rooma oma, mis kasutab numbritena ladina tähti:
Ma tähistan 1,
V-5,
X - 10,
L - 50,
C - 100,
D - 500,
M - 1000
Näiteks II = 1 + 1 = 2
siin tähistab sümbol I 1, olenemata selle kohast numbris.
Tegelikult pole Rooma süsteem täiesti mittepositsiooniline, kuna sellest lahutatakse näiteks väiksem number, mis tuleb enne suuremat numbrit:
IV = 4, samas kui:
VI = 6
Maiade numbrite süsteem
Vaata ka
Märkmed
Lingid
- Gashkov S. B. Numbrisüsteemid ja nende rakendused. - M.: MTsNMO, 2004. - (Raamatukogu “Matemaatikaharidus”).
- Fomin S.V. Numbrisüsteemid. - M.: Nauka, 1987. - 48 lk. - (Matemaatika populaarsed loengud).
- Jaglom I. Numbrisüsteemid // Kvant. - 1970. - nr 6. - Lk 2-10.
- Numbrid ja numbrisüsteemid. Interneti-entsüklopeedia kogu maailmas.
- Stahhov A. Arvusüsteemide roll arvutite ajaloos.
- Mikushin A.V. Numbrisüsteemid. Loengute kursus "Digiseadmed ja mikroprotsessorid"
- Butler J. T., Sasao T. Üleliigsed mitme väärtusega numbrisüsteemid Artiklis käsitletakse numbrisüsteeme, mis kasutavad ühest suuremaid numbreid ja võimaldavad arvude esitamisel liiasust
Wikimedia sihtasutus. 2010. aasta.
härjad (kategooriad). Seda lähenemist kasutatakse teabe edastamisel, salvestamisel ja töötlemisel ning tavaliselt ei seostata seda teabe semantilise sisuga.
1.5.2. Tõenäosuslik lähenemine
IN infoteooria, defineeritakse teavet kui ebakindlust, mis on eemaldatud. See võtab arvesse teabe väärtust adressaadi jaoks. Infohulga määrab see, kui palju väheneb määramatuse (entroopia) mõõt pärast teate saamist või sündmuse toimumist.
Infokoguse ühikuks (bitiks) loetakse infohulka, mis sisaldab sõnumit, mis vähendab teabe ebakindlust 2 korda. Üldjuhul määratakse teates sisalduva teabe hulk (H), mille kohaselt on aset leidnud üks N võrdselt tõenäolisest sündmusest, järgmiselt:
8 bitist koosnevat rühma nimetatakse baidiks. Kui bitt on minimaalne teabeühik, siis bait on peamine. Seal on tuletatud teabeühikud:
1 bait = 8 bitti;
1 kilobait = 210 baiti = 1024 baiti;
1 megabait = 220 baiti = 1024 kilobaiti;
1 gigabait = 230 baiti = 1024 megabaiti;
1 terabait = 240 baiti = 1024 gigabaiti.
1.6. Arvutiteaduses kasutatavad numbrisüsteemid
Numbrisüsteem on tehnikate ja reeglite kogum numbrite kirjutamiseks numbrite abil. On olemas mittepositsioonilised ja positsioonilised arvusüsteemid.
IN Mittepositsioonilises numbrisüsteemis on igal sümbolil oma kindel tähendus, mis ei sõltu sümboli asukohast numbrikirjes. Näiteks rooma numbrisüsteemis
I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000. Arv 77 on kirjutatud LXXVII.
IN Positsioonilises numbrisüsteemis sõltub iga numbri väärtus arvu kujutisel selle asukohast (positsioonist) antud arvu tähistavas numbrite jadas. Näiteks: 77 - 7 ühikut ja 7 kümnendikku.
Igal positsiooninumbrisüsteemil on mis tahes arvu tähistamiseks rangelt määratletud arv sümboleid (numbrid):
– binaarne – 2: 0 ja 1;
– koma – 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Numbrite arvu, mida positsiooninumbrisüsteemis kasutatakse numbrite kirjutamiseks, nimetatakse numbrisüsteemi baasiks. Arvusüsteemi aluseks võib olla mis tahes naturaalarv.
Olgu q süsteemi alus, siis saab arvusüsteemis mistahes arvu, mille alus on q, esitada järgmiselt:
A q = a n q n + a n –1 q n –1 + ... + a 1 q 1 + a 0 q 0 + a –1 q –1 + a –2 q –2 + ... + a –k q–k , (3) kus A q on arv, mis on kirjutatud arvusüsteemi alusega q,
n + 1 - arvu täisarvulise osa numbrite arv,
ja i on arvu numbrid, kus 0 ≤ a i< q ,
k - numbrite arv numbri murdosas.
Arvutiteaduses kasutatakse ainult positsioonilisi arvusüsteeme: kümnend, kahend, kaheksand, kuueteistkümnend.
1.6.1. Reeglid arvude teisendamiseks ühest numbrisüsteemist teise
1. reegel. Täisarvulise kümnendarvu A teisendamiseks alusega q arvusüsteemiks tuleb arv A jagada alusega q, kuni saadakse terve jääk, mis on väiksem kui q. Saadud jagatis tuleks uuesti jagada q-ga, kuni saadakse q-st väiksem jääk jne. kuni viimane jagatis on väiksem kui q. Seejärel tuleks kümnendarv A arvusüsteemis alusega q kirjutada jagamisjääkide jadana nende laekumise vastupidises järjekorras, kusjuures viimase jagatise annab kõrgeim number.
2. reegel. Kümnendmurru teisendamiseks alusega q arvusüsteemiks korrutage see arv alusega q. Korrutise täisarv osa on arvu esimene koht numbrisüsteemis alusega q. Seejärel, visates kogu osa, korrutage uuesti alusega q jne. kuni uues numbrisüsteemis vajaliku arvu numbrite saamiseni või tõlke valmimiseni.
3. reegel. Kümnendarvusüsteemi segaarvud tõlgitakse kahes etapis: eraldi täisarvu osa oma reegli järgi ja eraldi murdosa oma reegli järgi. Seejärel kirjutatakse üles koondtulemus, mille murdosa eraldatakse komaga.
4. reegel. Arvu teisendamiseks alusega q arvusüsteemist kümnendarvusüsteemiks tuleks kasutada arvu kirjutamise vormi kujul (3).
5. reegel. Täisarvu teisendamiseks kahendarvusüsteemist kaheksandsüsteemi on vaja erineva suurusega kahendnumbrite jada.




 Lugu lenduritest, kes pommitasid Hiroshimat ja Nagasakit
Lugu lenduritest, kes pommitasid Hiroshimat ja Nagasakit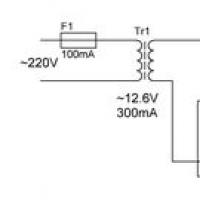 Sujuv võimsusega laadimine: mida valida?
Sujuv võimsusega laadimine: mida valida?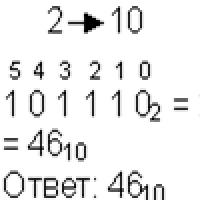 Väike matemaatikateaduskond
Väike matemaatikateaduskond "Miks unistate unes ümartantsust?
"Miks unistate unes ümartantsust? Miks unistate kirikust sees: unenäo tähenduse tõlgendamine erinevate meeste ja naiste unenägude raamatute järgi
Miks unistate kirikust sees: unenäo tähenduse tõlgendamine erinevate meeste ja naiste unenägude raamatute järgi Hurma unenägude tõlgendus, miks unistate unes hurmast, et näha unes hurma, miks
Hurma unenägude tõlgendus, miks unistate unes hurmast, et näha unes hurma, miks Nõiutud hing Karmanumbrite tähendus
Nõiutud hing Karmanumbrite tähendus